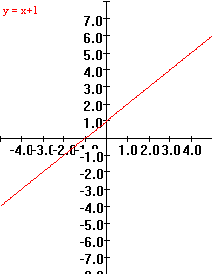1. Preface
2. Introduction to the Sensible Calculus Program
3. The Agenda and Vision
4. The Sensible Calculus Program Approach
1. Visualizations and Transformation Figures
2. Differential Equations, Tangent Fields, and Euler's Method.
3. Models
4. Taylor Theory
5. Probability
6. Technology
5. A Partial List of Features
6. Detailed Proposed Table of Contents
7. Sample Sections for Previewing
8. Comparison with Market Competition (Draft)
9. Bibliography  

   ---

Introduction to the Sensible Calculus Program (SCP): The Sensible Calculus Program reflects work of over twenty years by Professor Martin Flashman that started in developing a thematic approach to the first year of calculus. (See [MAA,4].)  Recognizing that a reform of the college precalculus function/algebra course would yield extra benefits in the success of calculus students, in about 1990 Professor Flashman expanded the vision of the program to include calculus preparation. The goal of the current project  is the creation of a precalculus and a calculus textbook and a full calculus program with a consistent thematic and conceptual approach. The program will prepare students in the precalculus component for learning calculus by providing motivation, background, concept development, and opportunities for real learning. The calculus component will build on these foundations with an approach that extends precalculus maturation into calculus. Two (among several) distinctive features of the SCP approach will apply to both the precalculus and calculus components:  

1. The extensive use of transformation figures (mapping figures) to visualize functions along with the traditional use of graphs, and
2. The early and consistent treatment of modelling contexts with a meaningful connection to issues of  continuous probability that explore the power of mathematics.

The Agenda and Vision. Calculus projects over the passed fifteen years have tried to improve the quality of calculus instruction with approaches mixing technology, pedagogical tactics, and curriculum revisions. As a result there has been much progress in rethinking the essential elements for a successful calculus program, leading to a general acceptance of many features of the reformed calculus agenda. Here is a brief statement of the current agenda and vision that the SCP addresses and which provide the fundamental direction for The Sensible Calculus Book.  

1. Define clearly and follow organizing concepts and principles for the content of the course;
2. Provide a consistent distinction between motivation, interpretation, and the mathematical concepts of calculus;
3. Connect the numerical, visual, and symbolic aspects of the calculus (called by some the "rule of three");
4. Encourage students to communicate as they solve problems (the "fourth" rule);
5. Use current technology to enhance concepts, not merely to facilitate mechanical approaches to computation, graphing, or symbolic manipulation;
6. Use applications, conceptual explorations, and history to weave together the many strands of mathematics;
7. Provide opportunities for students to control their own learning and understanding and to be creative while expressing their own views; and
8. Improve student backgrounds and motivation before calculus.

The Sensible Calculus Program Approach: The SCP focuses on the themes of differential equations [FL] and estimation throughout the first year of calculus, using modelling as a central motivation for applications of the calculus [FL2]. In the subsequent third semester or fourth quarter study of the calculus of several variables and the vector calculus these themes continue making an altogether unified and coherent approach to calculus. These themes and motivation have gained general approval from many of today's best selling textbooks. Unfortunately, there is no book today that succeeds in presenting the calculus consistently with these underlying principles. Along with thematic consistency, an important and unique pedagogical feature of the SCP text is the consistent use of interpretations to provide meaning for calculus concepts. Frequently examples of models or arguments will be presented before more general applications and proofs. This organization is based on the pedagogical principle that students can understand the specific and particular in experience and then generalize more easily then they can understand a general proposition or proof and the apply it to the particular.  

1. A geometric view using cartesian graphs to visualize functions, and
2. A dynamic/motion view using transformation figures (mapping figures) to visualize functions. (See Figure 1 for some examples of  transformation figures and corresponding graphs.)

Figure 1. Examples of  Cartesian Graphs and Transformation Figures with Tables. 

x f(x) = x+1 2 3 1 2 0 1 -1 0 -2 -1
x f(x) = x 2 2 4 1 1 0 0 -1 1 -2 4
x f(x) = -2x+1 2 -3 1 -1 0 1 -1 3 -2 5

 

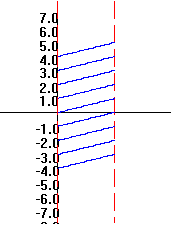
A transformation figure visually distinguishes the argument of a function from its value by repesenting each as a point on distinct parallel source (a on the X-Axis) and target lines (b on the Y- axis). These points are then connected with a line segment or an arrow joining a and b. This visualizaton is in contrast to the traditional Cartesian graph that consolidates the argument and function value visually at a single point (a , b), located at the intersection of lines, X = a and Y = b. Many students in their first calculus course are still developing their basis for understanding the function concept. The combination of transformation figures with Cartesian graphs gives a dual approach to interpreting and visualizing functions that has been particularly helpful for these students.  It also is a great aid in making sense of many calculus concepts and results, such as the chain rule and the differential. To make effective use of these visual tools the SCP employs them not merely in one or two instances as some current texts, but regularly invokes them in a variety of contexts [FL1]. This is central to the visually and conceptually balanced approach of the SCP.  

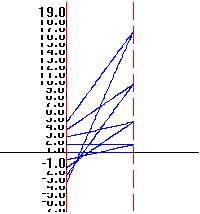
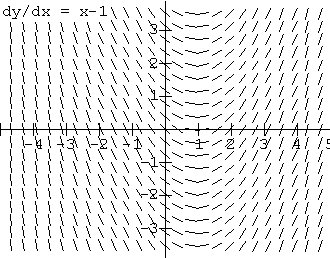
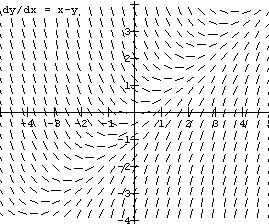
Differential Equations, Tangent Fields, and Euler's Method. The use of tangent (direction)  fields (see Figure 2 )  to visualize differential equations and Euler's method for estimating solutions to initial value problems (see Figure 3 ) are elements of the calculus curriculum that have won general acceptence in that past ten years as evidenced by their inclusion the current Advanced Placement syllabus and the best selling texts. Professor Flashman recognized the importance of these tools for understanding the calculus early in his development of The Sensible Calculus Program and has worked over twenty years with students to find presentations for these tools that are direct and easy to follow. As a result of all this experience, The Sensible Calculus Book combines an early and extensive discussion of differential equations with a visual approach through tangent fields  [FL2] and a numerical approach using Euler's method  [FL1].  Throughout the text the combined numeric and visual approaches complement  conventional symbolic discussions in topics such as solving indefinite integrals, motivating the definite integral and the Fundamental Theorem of Calculus, finding precise function solutions to initial value problems, and even more advanced symbolic techniques such as the separating variables.  
  
  
 

Figure 2: Examples of tangent fields for differential equations. 

Tangent Field for y' = x - 1.

Tangent Field for y' = x - y.

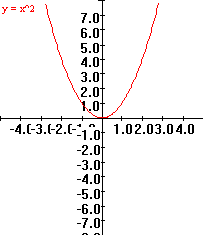
Models: Connecting applications of the calculus to the real world is not new. For centuries the calculus has been used to understand and plan in science and engineering. In traditional calculus texts, geometric and physical applications appear as motivation primarily for the calculus concept of the derivative. Otherwise applications usually appear only after a technique or concept has been presented. The Sensible Calculus Book  presents applications as a part of the modeling process in many contexts, both traditional and more contemporary, especially in economics and continuous probability. These contexts a threaded throughout the text, from the initial chapters on functions and the motivation of the derivative, to the first sections on differential equations and the introduction of both the indefinite and definite integrals, to the understanding of applications of the definite integral and the use of Taylor theory and concepts of infinite series. 

Frequently a model is presented for motivation and exploration before the calculus concept or technique as in the treatment of transcendental functions with differential equations.  For example, a heuristic model for learning introduces a differential equation context. The basic premise is that the rate of learning is often a positive yet decreasing function of time, for instance i) L'(t) = 1/t with t > 0  or ii)L'(t) = 1/[t² + 1] .  For the first equation, after a consideration of units and time scales, the boundary condition L(1) = 0 is established. Questions such as what will be the short and long run behavior of the learning function are investigated using tangent fields and Euler's method, as well as the derivative form of the Fundamental Theorem of Calculus. All this leads to a treatment of the natural logarithm function in the context of a differential equations model for learning.  

Likewise population (exponential growth and predator-prey) models motivate the exponential and trigonometric functions. All of these functions are treated with their traditional definitions as well. The object of the modeling approach is not to give formal rigorous treatments of these functions, but to show how the common functions arise and/or remain significant because they solve modelling problems expressed with differential equations.  Second order differential equations and population models motivate the hyperbolic functions as student investigations.  

Taylor Theory: Polynomial functions and geometric series have been a part of the calculus since the earliest work of Newon and Leibniz that has developed into what is now described as "Taylor theory."  The Sensible Calculus Book approaches Taylor theory as a distinct and important part of calculus, not a mere appendage at the end of a year's course treatment of infinite series. The text's development is based on the unifying themes of differential equations and estimation. The calculus of Taylor polynomials (not series) appears as a tool for approximating difficult definite integrals such as ∫₀¹ e ^{-x^2} dx with a sensible control on the error. Estimating the solution to differential equations such as y'' = -y or y''= y with y(0) = 1 and y'(0) = 1 [ which characterize the cosine and the hyperbolic cosine functions] provides additional motivation for the convergence questions of infinite series. Here again the problems we want to solve are placed  in the text before the techniques or theory.  Infinite sequences and series analysis discuss Taylor theory examples from the beginning along with the traditional examples of geometric and harmonic series. Historical connections Newton's work in estimating the values of the natural logarithm illustrate how geometric series played a significant role in the showing the power of the early calculus for computation and estimation. 

Probability: One of the most important applications of the calculus in current science and engineering is its use as a foundation for understanding probability and statistics. The inclusion of a section or two on this application in the best selling texts demonstrates the increased awareness by authors and teachers of the importance of this application. The Sensible Calculus Book does more then include a token section on probability and calculus. It includes continuous probability in the development of concepts of both differential and integral calculus.  

Starting with a simple experiment of throwing a dart at a unit circle in the background pre-calculus sections, the text develops the distance from where the dart lands to the center of the circle as a random variable for further investigation. Trying to understand the distribution function for this random variable eventually leads to its density function, i.e., its derivative. The text treats probability concepts frequently as interpretations of the calculus. The evaluation form of the Fundamental Theorem of Calculus shows the integral relation of the distribution function to the density function. Other probability concepts, such as the median, mode, and mean are introduced with an appropriate calculus concept.  

The Sensible Calculus' unique approach to probability follows the philosophies of both the NCTM Standards and the California Framework that call for the exploration of probability concepts as a regularly encountered strand in the fabric of mathematics. Whether a student is planning to be an engineer, a physician, or some kind of scientist, one of the most useful parts of their mathematics training will be probability and statistics. Making probability more relevant throughout the course allows students to see the interaction of calculus with this universal application. It enriches their understanding of both subjects as well as showing the application of continuous mathematics to nondeterministic situations.  

Technology: Though the SCP is not committed to any specific technology, it presumes access to technology capable of graphing and computation as well as some programming features in the event that computation or visual features are not predesigned in the technology.The text is not driven by technology, but it does presume (through its problem sets) that students and teachers will use technology to explore and enhance concepts as well as to solve problems.  
  

Pedagogy:  

• Consistent and balanced use of transformation (mapping) figures with cartesian graphs to visualize functions and calculus concepts.
• Learning builds from experience with examples to generalization and abstraction.
• Meaningful use of history to introduce and develop concepts.
• Technology used to enhance exploration of concepts with rule of three.
• Different assignment formats: team assignments, journals, outside reading, research assignments, oral presentations (not yet incorporated in the text).
• Synthesizing applications that put together many tools to explore a particular application in detail. [ The integral of exp(-x ²)]

• Early tangent fields and integral curves to visualize differential equations and solutions.

Example: Draft of Section on Tangent Fields.  
• Euler's method for numerical estimation of solutions for differential equations visualized with tangent fields and transformation figures.

Example: Draft of Section on Euler's method .  
• Differential equation and area motivation for the definite integral.
• Methods of integration
• connected to applications and modelling problems
• visualized using tangent fields
• Model motivation (DE's) for transcendental functions (exp, ln, trig, and inverse trig)

Examples: Draft of Section VI.A connecting differential equations to the exponential function and Section VI.B connecting differential equations to the natural logarithm function. Draft of VI.C  connecting the natural logarithm and exponential functions.

• Taylor Theory applications without reliance on infinite series.

Example: Draft of Section IX.A introducing Taylor Theory for e^x with applications.  
• Analysis of infinite sequences and series explains prior calculus experience.
• Series focus on applications to themes of estimating functions, definite integrals and solution to differential equations .

Example: Draft of part of Section  X.B Series: Some Key Examples.

• Probability as a consistent interpretation for the calculus.
• The distribution of a continuous random variable as the primitive concept for probability.
• The density function presented as the derivative of the distribution function.
• Median and mode related to calculus concepts.
• The Fundamental Theorems of Calculus interpreted with density and distribution functions.
• The mean of a random variable introduced without weighted averages.
• Expected value and variation.
• Normal Curve parameters
• Probability and infinite series.

[FL1] Flashman, Martin. "Computer Assisted Calculus And Themes for A Sensible Calculus," in Calculus and Computers: Toward a Curriculum for the 1990's, The Report of A Conference on Calculus and Computers Held at the University of California at Berkeley, August 24-27, 1989.  

[UMAP] Flashman, Martin. "A Sensible Calculus.," The UMAP Journal, Vol. 11, No. 2, Summer, 1990, pp. 93-96.  

[FL2] Flashman, Martin. "Using Computers to Make Integration More Visual with Tangent Fields," appearing in Proceedings of the Second Annual Conference on Technology in Collegiate Mathematics, Teaching and Learning with Technology of November 2-4, 1989, edited by Demana, Waits, and Harvey, Addison-Wesley, 1991.  

[FL3] Flashman, Martin. "Concepts to Drive Technology," in Proceedings of the Fifth Annual Conference on Technology in Collegiate Mathematics, November 12-15, 1992, edited by Lewis Lum, Addison-Wesley, 1994.  

[FL4] Flashman, Martin. "Historical Motivation for a Calculus Course: Barrow's Theorem," in Vita Mathematica: Historical Research and Integration with Teaching, edited by Ronald Calinger, MAA Notes, No. 40, 1996.  

[MAA,1] Committee on the Undergraduate Program in Mathematics, "Recommendations for a general Mathematical sciences program," Mathematical Association of America, Washington,1981.  

[MAA,2] Douglas, Ron, editor. Toward A Lean And Lively Calculus. MAA Notes, No. 6, 1986.  

[MAA,3] Steen, Lynn, editor. Calculus for a New Century: A Pump, Not A Filter. MAA Notes, No. 8, 1988.  

[MAA,4] Tucker, Thomas W., editor. Priming the Calculus Pump: Innovations and Resources. MAA Notes, No. 17, 1990.  

[MAA,5] Solow, Anita E., editor. Preparing for a New Calculus: Conference Proceedings. MAA Notes, No. 36, 1995.  

[MAA,6] Tucker, Alan C. and Leitzel, James R.C., editors. Assessing Calculus Reform Efforts: A Report to The Community. MAA Reports, No. 6, 1995.  

[MAA,7] Roberts, A. Wayne, editor. Calculus: The Dynamics of Change. MAA Notes, No. 36, 1996.  

[S&J] Swann, Howard and Johnson, John. Prof. E. McSquared's Calculus Primer, Janson Publications Inc., 1989.