IV.H Appendix. Proof of FTof C

IV.H APPENDIX: The Fundamental Theorem of Calculus: Proof for Positive Continuous Functions.

Here is a proof of the first draft version of the Fundamental Theorem announced in Section IV.H. It follows the same argument presented in Example IV.G.3 without much substantial change in the organization or the key concepts. If you feel ambitious you might try to create this proof on your own with Example IV.G.3 as a template.

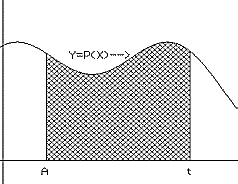
Theorem IV.4. [The Fundamental Theorem Of Calculus For Differential Equations]
Suppose that P is a positive continuous function on [A,B].
Then there is a function F so that F'(t) = P(t) for all t where A < t < B.
In fact, F can be defined at x = t to be the area of the region enclosed by the X-axis, the graph of the function P (i.e., Y = P(X) ), the line X = A, and the line X = t. See Figure IV.HA.i.

Figure IV.HA.i

Proof: For t > A let F(t) denote the area of the region enclosed by the X- axis, X = A, X = t, and Y = P(x).
Notice that F(A) = 0 because the "region" in this case is a line and its area is 0.
We must show that F'(a) = P(a) for a > A, so that F is a solution for the differential equation for the interval [A,B]

We interpret the expression F(a+h) - F(a) when h > 0
Consider the graph in Figure IV.HA.ii. On this graph the region enclosed by the X-axis, X=a, X = a+h, and the graph of Y = P(X) has area F(a + h) - F(a).

Figure IV.HA.ii

Examining this region more carefully in Figure IV.HA.iii, we notice that since P is continuous on [a, a + h], P will have extreme values.

Figure IV.HA.iii

We let c_* and c^* denote the points in [a, a + h] where P has its minimum and maximum values.
Furthermore the region we are considering lies inside the rectangle with base the segment of the X-axis between X = a and X = a + h and height P(c^*).

The region also contains the rectangle with base the segment of the X-axis between X = a and X = a + h and height P(c_*). This geometric situation means that

P(c_*)h < F(a + h) - F(a) < P(c^*)h,

thus P(c_*) < [F(a+h) - F(a)]/h < P(c^*). But because of the continuity of the function P, as $h \to 0$, $c* \to a$ and $c^* \to a$, so $P(c*)\to P(a)$ and $P(c^*)\to P(a)$. Thus, by the Sandwich Lemma of Chapter I, we have

[Remember, we assumed h > 0.] It can be shown similarly that

to
Thus

E.O.P.

Notes: 1. Another proof of this result in a slightly more general setting is given in the next chapter.

2. Geometric Interpretation of F'(a) = P(a): This result has the same informational content as Barrow's Theorem discussed in Chapter 0. At this stage you might review the statement of Barrow's Theorem in terms of how to draw the tangent line at a point on the area curve determined by a given curve and the X-axis. Under an appropriate interpretation of the derivative as the slope of the tangent line, the proof of Barrow's Theorem given in the appendix to Chapter 0 gives a geometric argument that can be modified to justify Theorem IV.4 as well.

3. Velocity Interpretations of F'(a) = P(a): Consider P as a velocity function for some moving object, X, and F as a position function for another moving object,Y, with its position at time t being equal to the area of the region described in the theorem. Under this interpretation, the inequality

P(c_*) h < F(a+h) - F(a) < P(c^*)h expresses a statement that the actual change in position of object Y for the time interval [a,a+h] will be between the distance travelled by an object always moving at object X's smallest velocity and the distance travelled by an object always moving at object X's greatest velocity.

Under the same interpretation, the inequality

P(c_*) < [F(a+h) - F(a)]/h < P(c^*) expresses the statement that the average velocity for object Y on [a,a+h] is between the minimum and maximum instantaneous velocities of object X for that interval. Thus when h is close to zero, the instantaneous velocity of Y will be close to P(a)!