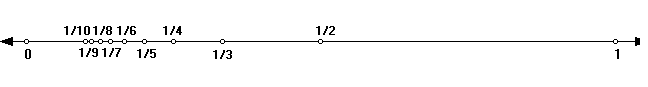
Preface: Throughout this introduction to calculus we have found that estimates could be improved by some process determined by a natural number `n`. In our estimates for solving equations this number `n` denoted the number of steps we would follow in using either the bisection method or Newton's method. Later `n` was the number of steps we used in Euler's method to estimate the value of the solution to a differential equation with given initial (or boundary) condition. Later still we found `n` controlling the size of intervals and the quality of estimates for the value of a definite integral with the trapezoidal rule and Simpson's rule. The number `n` also was used in estimating the values of many measurable quantities in applications, such as area and volume, allowing us to connect real situations to the mathematical concepts of derivative and integral. Finally, in the last chapter we found `n` indicating the degree of the MacLaurin and Taylor polynomials and their remainder terms which gave estimates for values for functions, integrals and solutions to differential equations.
The mathematics of real number sequences concerns the study a collection of real numbers determined in an order by a counter or index number, often denoted by `n`. The mathematical issues entail the description of these sequences and their properties.
One crucial question considers whether there is a tendency in the sequence for its members associated with larger natural numbers to approach a particular value called the limit of the sequence. There are actually two important and related questions:
(1) Is there a limit for a particular sequence?
For example, we are fortunate sometimes when we can use the Fundamental Theorem of Calculus to determine the precise value of the limit of numbers arising from Simpson's Rule for estimating a definite integral. Or in other situations we can use the Taylor Theorem to recognize that `1 + 1 + 1/2+ 1/6 + 1/{4!} + … + 1/{n!}` is approximately `e`. And we shouldn't forget that the sequences that arise from Newton's method for estimating solutions to equations (square roots, etc) frequently converge to numbers that are well described but known primarily by their estimates.
| {`a_n : n = 0,1,2, …` } | {`b_k`}`k = 0,1,2, …` | {`c_k`}`k = 1,2,3, …` |
| {`x_ n`}`n = 0,1,2, …` | {`y_n`} `n = 0,1,2, …` | {`s_n`} `n = 0,1,2, …` |
A typical defining statement for a sequence is `a_n
= f(n)` where `f` is some function defined at least on the
natural numbers.
For example `a_n = n^2`, `b_n
= 1/{n+1}`; `x_k = 1/{k!}`; and `s_n =
sum_{k=0}^{k=n}1/{k!}`.
It is also possible to define a term of a sequence using
previous
terms, such as `r_0=2` and for `k>=0, r_{k+1} = {r_k^2 +
2}/{2r_k}`
[Coming from Newton's method to approximate the square root of 2.]
Another example
of this sort is the sequence defined by `f_0=1, f_1=1` and
`f_{k+2}=f_k + f_{k+1}`, creating the sequence
`1,1,2,3,5,8,13,....` often described as (Leonardo Pisano)
Fibonacci's
sequence (1170 - 1250) .
An even more general example would allow the sequence to have a
real
variable in its definition, such as the sequence
Visualizing sequences: There are many ways to think about real number sequences and each way leads to a visualization of the sequence that can assist in making the sequence and its properties more apparent.
First, a real number sequence is a set of real numbers
together with
an order for these numbers. With this in mind we can display
the
sequence as a collection of points on a real number line.
The
order of the points can be seen by labeling the points with the
subscripts
that indicate there relative
order, such as `a_1, a_2, a_3, …` .
Example. X.I.A
A visualization of the sequence {`1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7,
1/8,
1/9, 1/10, ..., 1/k ,...`}
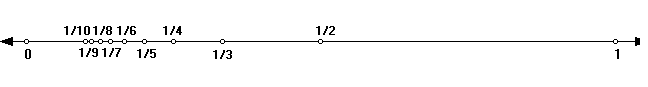
Another way to indicate the order is to draw an arrow from one point to the next on the line, so we see a succession of arrows above the number line each showing which number is next in the sequence.

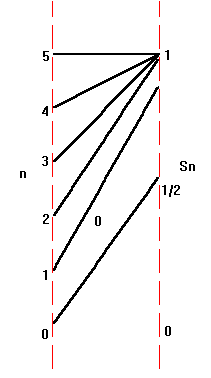
Convergence. The values of a real number sequence can be interpreted as numbers that occur in some order, as the image values in a mapping diagram with the indices increasing, or as points on the graph of the sequence.
One issue that is very important in the study of sequences is whether the values of the sequence {`a_n`} `n=0,1,2, …` approach a limiting number, `L`, when `n` is very large. If this is the case we write that `a_n -> L` as `n ->oo` or `lim_{n->oo}a_n = L` and we say, "The sequence an converges to L as n goes to infinity."
Examples. Let `a_n = n^2` ,`b_n
=1/{n+1}`, `c_n = {4n^2} /{7 n^2 - 5n
- 2}`, and `S_n = cos(1/{1 + n^2 })`.
Discussion: These sequences might also be described directly
as { `n^2` }`n = 0,1,2, …`; { `1/{n+1}` }`n
= 0,1,2,…`; `{4 n^2} /{7 n^2
- 5 n - 2}`
`n = 0,1,2, …`; and `cos(1/{1 + n^2}) n
= 0,1,2,` …. Table X.A.1 shows some of
the
initial values for the sequences while the figures below show in
part the mapping diagrams and graphs for initial values of
the latter three
sequences.
 |
 |
 |
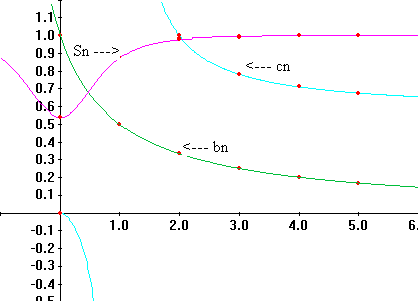 |
Without being rigorous at this stage, it should make sense that
there
are limits for all but the first of these sequences. In particular
`lim_{n->oo}1/{n+1} =
0 ; lim _{n->oo}{4n^2}
/{7 n^2-5n-2}= lim _{n->oo}{4}
/{7 - 5/n - 2/{n^2}}= 4/7`; and `lim _{n->oo}cos(1/{1 +
n^2 }) = 1`.
Examples from Euler's method and Riemann sum integral approximations.
Example. A sequence that converges to `e`. Recall that in considering the differential equation `y'=y` with `y(0)=1` we estimated the value of `y(1)` using Euler's method in `n` steps to be `(1+1/n)^ n`. With `n` larger we obtain better estimates for `y(1)=e`. Thus we can conclude that as `n->oo, (1+1/n)^ n -> e`.
Example. A sequence that converges to `ln(2)`. In
considering the
differential equation `y'=1/x` with `y(1)=0`, using Euler's method
in
n steps, we estimated
`y(2)~~ 1/n [1 +
n/{n+1} + n/{n+2} + …. + n/{2n-1}] = 1/n + 1/{n+1} + … + 1/{2n-1}
= S_n`.
Thus as `n->oo, S_n ->
y(2) = ln(2)`. Notice that this sequence is also the sequence of
left hand
endpoint Riemann sum estimates of the definite integral `int_1^2
1/x
dx`.
Example. A sequence that converges to `1/2`. For a simpler example we can consider `S_n = 1/n [ 1/n + 2/n + …. + {n-1}/n]`, the left hand Riemann sum estimate for the definite integral `int_0^1 x dx = 1/2` . Thus as `n->oo, S_ n-> 1/2`.
Examples from Taylor approximations.
Example. Another sequence that converges to e. Recall that
in
considering the differential equation `y' = y` with `y(0)=1` we
estimated the
value of `y(1)` using Taylor (Maclaurin) polynomials of degree `n`
evaluated
at `x=1`. If we let `S_n = P_n
(x) = 1 + 1 + 1/2 + 1/{3!}
+ 1/{4!} + ... + 1/{n!}`, then with n larger we obtain
better estimates
for `y(1)=e`. [In fact we actually have a measure of the
difference between
`e` and `S_n`
given by `R_n = e - S_n` as in the
work on Taylor Theory in chapter IX.] Thus we can conclude that as
`n->oo,
S_n -> e`. Furthermore, the same
theory explains why for each x, the sequence
`S_n = P_n
(x) = 1 + x + {x^2}/2 + {x^3}/{3!}
+ {x^4}/{4!} + ... + {x^n}/{n!}` converges
to `e^x` as `n->oo`..
Example. A sequence that converges to `ln(1.1)`. Recall that in considering the differential equation `y' = 1/x` with `y(1)=0` we estimated the value of `y(1.1)` using Taylor polynomials of degree `n` about `x=1` evaluated at `x=1.1`. If we let
Exercises X.A.
For each of the following sequences, (a) list the first five values,(b) draw a mapping diagram for the first five values, (c) draw a graph for the first five values, and (d) find the limit as `n->oo` when possible.
1. `((5n^2 + 3n -2)/(2n^2 + 3n -1)) _ {{n = 0,1,2 ...}}`.
2. ` sin( (3n -2)/(2n^2 + 3n -1)) _ {{n = 0,1,2 ...}}`.
3.`((4n + 2)/(3n^2 + 2n -1)) _ {{n = 0,1,2 ...}}`.
4. `((n^3 + 1)/(3n^2 + 2n)) _ {{n = 1,2 ...}}`.
5. (-1)n{n = 0,1,2 ...}.
6. (-1)n/(n2 + 1) {n = 0,1,2 ...}.
7. (2/3)n {n = 0,1,2 ...}.
8. (-2/3)n{n = 0,1,2 ...}.
9. e1/(n+1) {n = 0,1,2 ...}.
10. `tan^(-1)(1 - 1/(n+1)) _ {{n = 0,1,2 ...}}`.