IV.G. Differential Equations and Area: Variation on A Theme.
 © 2002 M. Flashman
Preface: By examining Euler's method in Section IV.F we found a method for finding the area of a region in the plane by solving a differential equation (finding an indefinite integral). We achieved this result by relating estimates for the solution of a differential equation with initial condition to rectangles whose area estimated the area of the planar region. In this section we'll examine a different relationship between area and solving differential equations. Our focus here is on a particular case related to Issue 1 identified in Section IV.A, namely,  the existence of a solution to a differential equation of the form F’(x) = P(x) where P is a continuous function.

From our previous interpretations of differential equations using position or cost functions, we can suggest the following affirmative result: any differential equation of the form F’(x) = P(x) where P is a continuous function has a solution. For a position interpretation, just imagine you control the movement of an object by adjusting its velocity so that at any time, t, its velocity is P(t). Then the resulting position function for the object solves the differential equation. Or for an economics interpretation, imagine producing some good stuff where the marginal cost of producing x units is P(x). Then the resulting accumulated cost function for production solves the differential equation.

The motion and cost interpretations can be visualized with transformation figures. In this section we will use an area interpretation to produce a function that solves a differential equation. The advantage of focusing on area is that an area interpretation comes with its own inherent visualization. We will assume in this discussion a naive understanding of the concept of area as a numerical measure of a planar region without any deeper investigation of its meaning. We will explore a deeper meaning for area in Chapter V. 

Motion and Area. We begin with some simple examples in the context of a moving object for which we know only the velocity and initial position.

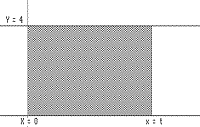
Example IV.G.1. [Constant velocity] Consider the differential equation: v(t) = s'(t) = 4 with initial condition s(0) = 0 where s denotes the position of an object moving on a straight coordinate line and v denotes its velocity. In other words, the object is moving at a constant velocity and started at the point with coordinate 0.
Using the notation of indefinite integrals, we can solve the differential equation symbolically. Since ò v(t) dt = ò   4 dt = 4t + C and s'(t) = v(t), we have that 
s(t) = 4t + C for some constant C (from Theorem 4.2). 
But s(0) = 0 implies that C = 0, so s(t) = 4t. [This solution should not be a surprise.]  Taking a cue from Chapter IV.F we sketch a graph of the velocity, v, as a function of t. (See Figure IV.G.i.) The shaded region which is enclosed by the X-axis, the lines X = 0 and X = t, and v = 4 has area 4.t, which is precisely the value of s(t). 		  Figure IV.G.i 
Figure IV.G.i
Comment: As we will see this example is no mere coincidence. It is also worth noting that we could find the area of this rectangle using Theorem 4.3, the Fundamental Theorem of Calculus.  The area would be the value s(t) – s(0) = 4t – 0 = 4t. 

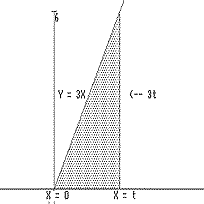
Example IV.G.2. [ Constant Acceleration]. We continue to look at velocity and position. This time use the differential equation s'(t) = v(t) = 3t with s(0)=0. Now our object has an increasing velocity and a constant acceleration. Again we can solve precisely for s(t). Since òv(t)dt = ò3t dt = (3/2)t 2 + C, we have (from Theorem 4.2) that s(t) = (3/2)t 2 + C. But s(0) = 0 implies that C = 0, so s(t) = (3/2)t 2 . 
Now in the graph of v of  Figure IV.G.ii  we observe that the shaded region (a triangle) which is enclosed by the X-axis, the lines X = 0 and X = t, and v = 3x has area equal to one half the base times the altitude of the triangle, i.e., (1/2)(t)(3t) = (3/2)t 2. So the area again is precisely the value for s(t). 		  Figure IV.G.ii 
Figure IV.G.ii
Comment: We could find the area of this triangle also by an application of Theorem 4.3, the Fundamental Theorem of Calculus. The area would be the value s(t) – s(0) = (3/2)t 2– 0 = (3/2)t 2. 
What was common to the last two examples? In each example the solution of the differential equation could be visualized as the area of a region in the plane defined by the graph of the velocity function. The next example demonstrates how to reverse this relation to solve differential equations. 
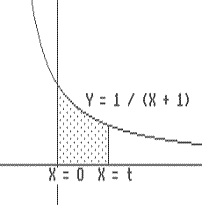
Example IV.G.3. [Solving a differential equation using an area function.]Consider a moving object with a positive velocity decreasing to 0. Perhaps we have observed that the object is slowing down (to a stop) but always continues to move. There are several possible equations that might model this situation. For this example let's consider  v(t) = s'(t) = 1/(t+1) where t > -1 and s(0)=0. The graph of v is in Figure IV.G.iii. 

Our problem is to describe at least one function that solves this differential equation for t > 0. Following the pattern suggested by the two previous examples, for t > 0 we let F(t) denote the area of the region enclosed by the X - axis, X = 0, X = t, and Y = 1/(x+1).  

Notice that F(0)=0 because the "region" in this case is a line segment and its area is 0. Recall that the work in Section IV.F demonstrated that estimates for the value of the position function, s(t), using Euler's method would also serve as estimates for F(t). Thus, it should seem reasonable that s(t) = F(t) and that 

F'(t) = 1/(t+1) for any t  ³ 0. 
  Figure IV.G.iii 
Figure IV.G.iii
Unfortunately we don't have any easy method at this stage of our work H for finding the area F(t) as an elementary function of t. So we can't check that F'(t) = v(t) from the derivative calculus we have developed so far for some of the elementary functions. However, by returning to the basic defining property of the derivative, we will show that F'(a) = 1/(a+1) for any a > 0
Thus F is a solution for the differential equation for the interval [0,¥). 
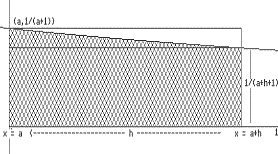
Justification that F'(a) = 1/(a+1) for any a > 0 : We begin by interpreting the expression F(a+h) - F(a) when h > 0. Consider the graph in Figure IV.G.iv. On this graph the region enclosed by the X-axis, X = a, X = a+h, and the graph of Y = 1/(X+1) has area F(a+h) - F(a).  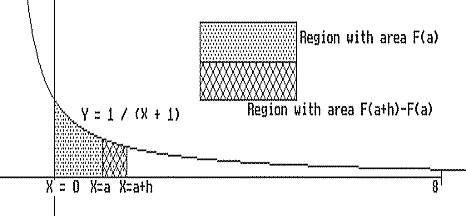 Figure IV.G.iv 
Figure IV.G.iv
Examining this region more carefully in Figure IV.G.v we see that 1/(a+h+1) . h < F(a+h) - F(a) < 1/(a+1) . h because the region is enclosed within a large rectangle with area h/(a+1) and encloses a smaller rectangle with area h/(a+h+1). 

Now to find F'(a) we consider [F(a+h) - F(a)] / h as h > 0. From the previous work we now see that for h > 0 

  Figure IV.G.v 
Figure IV.G.v
 
1/(a+h+1) < [F(a+h) - F(a)]/h < 1/(a+1)
so that 
[Remember, we assumed h>0.] It can be shown similarly that  Thus 
EOP.

HFinding a formula for this area function would be possible if we had an elementary function that solved the differential equation. In fact we will show later in Chapter VI that the logarithmic function ln(t+1) is a solution.
 Problems For problems 1- 8, consider v(t) as the derivative in a differential equation S'(t) = v(t). Sketch the graph of  v(t)  for the given differential equations. Let F(t) denote the area of the region enclosed by the X- axis, X = 0, X = t, and Y = v(x) with 0 £ x £ 3. On your sketch shade regions that have area F(2), F(2.1), and F(2.1)-F(2). Use an estimate of [F(2.1)-F(2)] /.1 to estimate F '(2). Compare this estimate with v(2).
    1. v(t) = 1 + 2t
    2. v(t) = t + 1
    3. v(t) = .5 t
    4. v(t) = t3
    5. v(t) = sin(t)
    6. v(t) = 2/(1+t)  -1< t
    7. v(t) = 1/(t 2+1)
    8. v(t) = t/(t2 + 1)
9 - 13. For the functions v given in problems 1-5, find (explicitly) a function S so that S'(t) = v(t) and S(0) = 0. Let F(t) denote the area of the region enclosed by the X-axis, X =0, X = t, and the graph of Y = v(x) with 0 £ x £ 3. Find F(2).

14 - 21. For the functions v given in problems 1-8, sketch a tangent field for the differential equation S'(t) = v(t). Sketch an integral curve on the field passing through the point (0,0). Use this integral curve to estimate the area of the region enclosed by the X? axis, X = 0, X = 2, and the graph of Y = v(x). Discuss the relation of the integral curve to the function F(t) which denotes the area of the region enclosed by the X-axis, X = 0, X = t, and Y= v(x).

22. Complete the discussion for F(t) being a solution to the differential equation v(t) = s'(t) = 1/(t+1) where t > -1 and s(0) = 0 by examining the situation with h < 0 and showing that
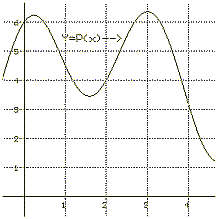
23. Suppose P(x) has a graph as given in Figure IV.G.vi and F(t) is defined as the area of the region enclosed by the X-axis, the Y-axis, the line X= t, and the graph of Y=P(x). 
a) Estimate F(2.1), F(2.1) - F(2), F'(2). 
b) Estimate F'(2), F'(3), F'(1). 
c) For what value of t do you think F'(t) is largest on the interval [0,4]? 
d) For what value of t do you think F'(t) is smallest on the interval [0,4]? 
e) Explain why F(t) is an increasing function on the interval [0,4]. 
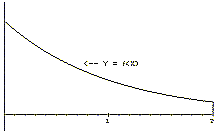f) Discuss the concavity of the graph of F. 		 Figure IV.G.vi 
Figure IV.G.vi 
24. For each of the following graphs suppose that the graph is the graph of a continuous probability density function f  for a random variable X with distribution function F on the interval [0,2].

a) Based on the fact that F'(A) = f (A), F(0)= 0 and F(2)=1, as a matter of definition, draw a sketch of the graph of F.
b) Estimate the probability that X is between 0 and 1.
c) Estimate the mode of X.
d) Estimate the median for X.
e) Estimate the values of A where F(A) = 1/4 and F(A) = 3/4.