X.B.5 Tests for Divergence and Convergence. ( in
Progress)
April, 2006: This page now requires Internet Explorer 6+MathPlayer or
Mozilla/Firefox/Netscape 7+.
©
2000 M. Flashman
In this section we'll consider some elementary and direct tests for
determining the question of convergence for an infinite series. These
tests
will be applied to examples of power series in an attempt to determine
the intervals on which the power series may converge called intervals
of
convergence.
Theorem X.B.1 (The Divergence Test). Suppose that
`sum_{k=0}^{oo}c_k` converges to S.
Then `lim_{k->oo}c_k = 0`.
Proof: Let `S_n = c_0 + c_1
+ c_2 + ... + c_k + ... + c_n = sum_{k=0}^{k=n}c_k` so that `S_n
=S_{n-1}
+ c_n`.
By the hypothesis we have that as `n->oo`,
`S_n-> `S and
also `S _{n-1}->S` as well. But
`c_n = S_n - S_{n-1}`,
so
as
`n->oo`
,
`c_n = S_n - S_{n-1}-> S -
S =
0`. EOP
Comments.
- This result is called the
divergence test because its use is primarily
to show that an infinite series does not converge, i.e., that it
diverges.
- Once again, don't forget the harmonic series. It shows that the
fact
that
`c_k ->0` is only a necessary consequence of the convergence of a
series,
but is not sufficient by itself as a condition to guarantee that a
series
converges.
- There is a test that applies to
alternating series which is almost a converse for this test. Review the
previous discussion on the alternating harmonic
series and see if you can state and justify such a result.
- The logic of necessary and sufficient
conditions is sometimes confusing in the way that these
conditions are expressed. One
traditional form is to say, "If condition A is true, then condition B
is true" or more simply: "If A then B." B is decribed as
the "necessary" condition, while A is described as the "sufficient"
condition. Knowing that condition A is true is sufficient to infer that
condition B is also true. Condition B is a necessary
condition - without it being true, condition A cannot be true. This
gives us the equivalent contrapositve
statement relating
conditions A and B, namely, " If condition B is not true , then
condition A is also not true" or more simply "If not B,
then not A."
Try thinking these connections through with the following choices for A
and B.
A: Ben earned a grade of A in the calculus course. B: Ben
passed the final examination in the calculus course.
A: Michael earned a grade of A in all his high school
courses. B: Michael earned a grade of A in his sophomore
High school English course.
A: Jennifer earned a doctorate degree in
Sociology. B: Jennifer passed the qualifying
exminations for the doctorate degree in Sociology.
A: The function `f` is differentiable at
`x=a`. B: The function `f` is continuous at `x=a`.
Example X.B.7.
(a) `sum_{k=0}^{oo}
k/{5k + 100}` diverges.
(b) If `| x | >= 1` then `sum_{k=0}^{oo}
x^k` diverges.
Discussion. (a) Apply the theorem to `c_k =
k/{5k + 100}`. As `k->oo`,
`c_k->1/5
> 0`. Therefore the series cannot converge.
(b) Since `| x | >= 1`, the sequences `| x ^k| ` and `x^k`
do not approach
`0`. [The term `|x^k|` is always at least `1`.] Hence the series
will not
converge
for those values of `x`.
The next test gives a very useful general test for convergence. Its
greatest use for us will be to find more mechanical tests for
convergence.
Theorem X.B.2 (The Foundation Test for Positive Series. "Bounded
if and only if convergent").
Suppose that `c_k > 0` for all `k`, then `S_n`
converges if and only if there some number `B`, for which
`S_ n = sum_{k=0}^{k=n} c_k < B` for any `n`.
Proof: Notice first that `S_n = S_{n-1}+ c_n` so `S_n
>S_{n-1}` for all `n`. Thus
the sequence `\{S_n\}` is an increasing sequence and from our
previous discussion on sequences, the sequence converges if and only
if there some number `B`, `S_n < B` for any `n`.
EOP.
We can apply this foundational result about positive series to justify
three useful tests for convergence.
Theorem X.B.4 (The Comparison Tests for Positive Series).
Suppose
that `c_k > d_k > 0` for all `k`.
(i) If `sum_{k=0}^{oo} c_k` converges then
`sum_{k=0}^{oo} d_k` converges.
(ii) If `sum_{k=0}^{oo} d_k` diverges then `sum_{k=0}^{oo}
c_k`
diverges.
Proof: First notice that since `c_k > d_k
>
0` for all `k` ,
`T_ n = d_0 + d_1 + d_2 +
... + d_ k + ... + d_ n < S_n = c_0
+ c_1 + c_2 + ... + c_k + ... + c_n`
for all `n`.
(i) Suppose `sum_{k=0}^{oo} c_k`
converges. Then by X.B.3, there is some number `B` where `B>S_ n
>T_ n` for all `n`. Now applying X.B.3 to the sequence` T_n`
completes the argument.
(ii) Suppose `sum_{k=0}^{oo} d_k` diverges . Then by part
(i) `sum_{k=0}^{oo} c_k` can not converge. Therefore
`sum_{k=0}^{oo} c_k` diverges.
EOP.
Example X.B.8: Consider
the series (i) `sum_{k=1}^{oo}
(.5)^k` , (ii) `sum_{k=1}^{oo}{(.5)^k}/{k+1}`,
(iii) `sum_{k=1}^{oo}1/k` , and (iv) `sum_{k=1}^{oo}
{3k}/{k^2+1}`.
For (i) and (ii) it should be clear that `{(.5)^k}/{k+1}<
(.5)^k` for `k=1,2,3, ...`, and `sum_{k=1}^{oo}
(.5)^k`
is a geometric series that converges. So by the comparison test,
`sum_{k=1}^{oo}{(.5)^k}/{k+1}` converges also
.
On the other hand for `k= 1,2,3,...` , `1/k <{3k}/{k^2+1}`.
[This is justified by observing that `k^2+1<3k^2`.]
Since `sum_{k=1}^{oo}1/k` diverges, we can apply X.B.3 to see that
`sum_{k=1}^{oo}
{3k}/{k^2+1}` diverges as well.
Theorem X.B.5 (The Integral
Tests for Positive Series).
Suppose
that `c_k > 0` for all `k` and for some decreasing
continous
function `f` , `f (k) = c_k`. Then the series `sum_{k=1}^{oo} c_k`
converges if and only if `int_{1}^{oo} f(x) dx` converges.
|
Proof: Consider the
following inequalities based on the fact
that `f(k)=c_k` and `f` is a continuous decreasing
function.
`c_2 < int _1^2 f (x)
dx < c_1`
`c_3 < int_2^3 f (x) dx < c_2`
`c_4 < int_3^4 f (x) dx < c_3`
...
`c_n< int_{n-1}^n f (x) dx
<c_{n-1}` |
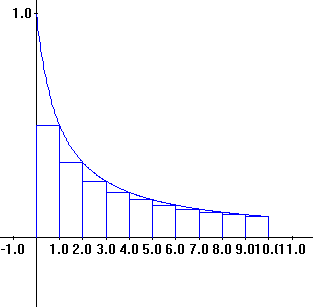 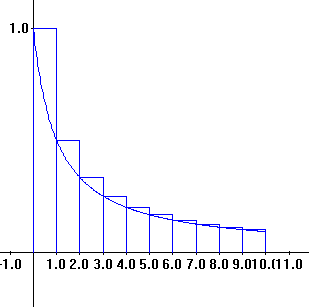
|
So
`sum_{k=1}^{k=n}
c_k =c_1
+c_2 +... + c_n < c_1 + int_1^2 f (x)dx + ...+ int_{n-1}^n f (x)dx =
c_1
+ int_1^n f (x)dx` (*)
while
` int_1^n f (x)dx = int_1^2 f
(x)dx+ ... +int_{n-1}^n f (x)dx <c_1
+c_2 +... + c_{n-1}= sum_{k=1}^{k=n-1}
c_k`. (**)
(i) Suppose `int_1^{oo}f
(x)
dx` converges to `I`. Then by (*) `sum_{k=0}^{k=n}c_k < I` for all
`n` and the series converges.
(ii) Suppose `int_1^{oo}f
(x)
dx` diverges. `I_n = int_1^n f (x) dx >0` and is increasing
for all
`n`. Since the integral diverges, these integrals, `I_n` and the
corresponding the
partial
sums `S_n =sum_{k=0}^{k=n}c_k` are not bounded. Therefore the
series diverges.
EOP.
Exanple
X.B.9. Consider
the series (i) `sum_{k=1}^{oo} 1/{k^2}` and (ii) `sum_{k=1}^{oo}
{2k}/{k^2+1}`.
(i) The function `f(x) = 1/{x^2}` satisfies the hypothesis of the
theorem. Thus we consider
`int _1^{oo} 1/{x^2} dx =
lim_{B->oo}int_1^B 1/{x^2} dx =
lim_{B->oo}- 1/x| _1^B = lim_{B->oo}1 - 1/B = 1`.
Since the
integral converges, we can apply the theorem to conclude that the
series
`sum_{k=1}^{oo} 1/{k^2}` also converges.
(ii) The function `f(x) = {2x}/{x^2+1}` satisfies the hypothesis of
the theorem. Thus we consider
`int _1^{oo} {2x}/{x^2+1} dx =
lim_{B->oo}int_1^B {2x}/{x^2+1} dx =
lim_{B->oo}ln(x^2+1) | _1^B = lim_{B->oo}ln(B^2+1)-ln(2) =
oo`.
Since the integral diverges, we can apply the theorem to conclude
that the series
`sum_{k=1}^{oo} {2k}/{k^2+1}` also diverges.
This next theorem compares a positive series with a geometric
series. In practice this is one of the most important tools we will
develop for determining when a series converges or diverges.
Theorem X.B.6 (The Ratio Test for Positive Series).
Suppose
that `c_k>0` for all `k` . Suppose that as
`k->oo`,
the ratios `{c_{k +1}}/{c_k}->
R`.
(a) If `R < 1` then the series `sum_{k=0}^{oo}c_k` converges.
(b) If `R > 1` or does not exist, there is no limit then
the series
`sum_{k=0}^{oo}c_k` diverges.
(c) If `R = 1` then this test can give no information on the
series
convergence.
Proof:
(b) We'll begin by considering the case when `R>1`.
In this situation when `k` is large, the ratios `{c_{k
+1}}/
{c_k}` are close to the number `R`. `R>1` means that
there is a number `B >1` where when `k` is large `{c_{k +1}}/{
c_k}
> B >1`.
Choose a number `N` that is large enough so that the last inequality
holds for all `k > N`.
Now since `c_N > 0` we can multiply to obtain that
`c_{N+1}>c_N * B >c_N > 0`.
In fact continuing this analysis for `c_{N+2}` we find that `c_{N+2}
>c_[N+1} * B >c_N * B^2 > c_N
> 0`.
In general you can see that for `k > N`, `c_k > c_N>0`.
But this means that as `k->oo` ,
`c_k` cannot be approaching `0`. Therefore the series
`sum_{k=0}^{oo}c_k` must diverge by
the divergence test.
(a) Now to consider when `R < 1` we pursue a similar analysis.
This time we see
that
there is some number `rho` with `rho < 1` where when `k` is
large
`0
<{c_{k +1}}/{c_k}< rho <1`.
Choose `N` large enough so that this last inequality is
true
for all `k > N`.
Then since `{c_{N+1}}/{c_N}< rho
<1`,
`c_{N+1}< c_N * rho <c_N` .
Similarly, `c_{N+2} < c_{N+1} * rho <
c_N * rho^2` .
Continuing we see that `c_{N+3}< c_{N+2} * rho <
c_N * rho^3`.
In general we have `c_{N+j}< c_{N+j-1}* rho< c_N * rho^j`.
Now we consider the geometric series `sum_{j=1}^{oo}c_N rho^j`.
This series converges to a number `L={c_N rho}/{1-rho}` because
`0
< rho < 1`.
(At this point we are not concerned with the actual value of L, only
that
such a number exists!)
Let `B = L + sum_{k=0}^{N}c_k`.
You can now check that for all `n`, `S_ n = sum_{k=0}^{k=n}c_k< B`
. Thus by the comparison test, the series converges.
EOP
Example X.B.10.
Use
the
ratio
test to determine the
convergence
of `sum_{k=0}^{oo}{3^k}/{ k!}`.
Solution:Being systematic in
applying the ratio test is often helpful in
avoiding errors. Here is one way to keep your work organized in a step
by step fashion:
Step 1: Write down `c_k`:`c_k
=
{3^k}/{
k!}`
Step 2: Write down `c_{k+1}`:.
`c_{k+1}= {3^{k+1}}/ {(k+1)!}`
Step 3: Write down and simplify the ratio,`{c_{k
+1}}/{c_k}`:
`{c_{k +1}}/{c_k}={{3^{k+1}}/
{(k+1)!}}/{{3^k}/{k!}}= {3^{k+1}*k!}/{3^k * (k+1)!}=3/ {k+1}`.
Step 4 : Think- find `R
=lim_{k->oo}{c_{k +1}}/{c_k}`:
Clearly as `k->oo`, `{c_{k
+1}}/{c_k}->0` so `R = 0`
Step 5: Use the ratio
test to draw a conclusion:
Since `R = 0` the series `sum_{k=0}^{oo}{3^k}/{ k!}` converges.
Note: The Taylor
polynomial of degree `n` for `e^x` evaluated at `3` is
`sum_{k=0}^{k=n}{3^k}/{ k!}`. It is an exercise at the end of this
section to examine the error terms for these polynomials and thus show
that `sum_{k=0}^{oo}{3^k}/{ k!}= e^3`.
Example X.B.11. The ratio test can show that the series
`sum_{k=0}^{oo}{x^k}/{ k!}` converges for
all
positive
values of x.
Following the work of the previous example we have
Step 1.`c_k = {x^k}/{ k!}`.
Step 2. `c_{k+1}= {x^{k+1}}/ {(k+1)!}`.
Step 3: Write down and simplify the ratio:
`{c_{k +1}}/{c_k}={{x^{k+1}}/
{(k+1)!}}/{{x^k}/{k!}}= {x^{k+1}*k!}/{x^k * (k+1)!}=x/ {k+1}`.
Step 4: Think. Find R: Clearly as `k->oo`, `{c_{k
+1}}/{c_k}= x/ {k+1}->0`,
so `R=0`.
Step 5. Use the ratio test: Since `R=0` for any `x>0`, the series
`sum_{k=0}^{oo}{x^k}/{ k!}` converges for any positive ` x`.
Remark: The Ratio Test Meets the
Divergence Test.
Combining the ratio test with the divergence test can make a
powerful tool for showing that a sequence converges to 0.
For instance, consider the last example in which the ratio test showed
that `sum_{k=0}^{oo}{x^k}/{ k!}` converges for all positive values of x. Now by the
divergence test we have that `lim_{k->oo}{x^k}/{
k!}=0` for all positive values of x.
But `|t|>0` for any real number `t` so `lim_{k->oo}{|t|^k}/{
k!}=0`.
And of course `|t|^k = |t^k|` so `lim_{k->oo}{|t^k|}/{
k!}=0`. Therefore `lim_{k->oo}{t^k}/{
k!}=0`
for
any real number t.
This last statement is very useful- especially in showing that `sum_{k=0}^{oo}{x^k}/{
k!}
=
e^x` for all `x`. [See exercise ***]
Example X.B.12. Find all
positive values of x for which the series
`sum_{k=0}^{oo}{(2x)^k}/{ k+3}` converges.
Solution: Again being
systematic in applying the ratio test is often helpful in avoiding
errors. Here is the way we have been proceeding in a step by step
fashion:
Step 1: Write down `c_k`:` c_k
= {(2x)^k}/{ k+3}`.
Step 2: Write down
`c_{k+1}`:.
`c_{k+1}= {(2x)^{k+1}}/ {(k+1)+3}`.
Step 3: Write down and simplify the
ratio,`{c_{k +1}}/{c_k}`:
`{c_{k +1}}/{c_k}={{(2x)^{k+1}}/{(k+4)}}/{{(2x)^k}/{k+3}}
= {(2x)^{k+1}*(k+3)}/{(2x)^k * (k+4)}=2x {k+3}/ {k+4}`.
Step 4 : Think- find `R
=lim_{k->oo}{c_{k +1}}/{c_k}`:
Clearly as `k->oo`, `{c_{k +1}}/{c_k}=2x {k+3}/
{k+4}-> 2x`,
so `R=2x`.
Step 5: Analyze when `R<1` and when `R>1`:
`R=2x
<1`
when `0<x<1/2` and `R>1` when `x>1/2`.
Step 6: Use the ratio test to
draw a conclusion:
The series `sum_{k=0}^{oo}{(2x)^k}/{ k+3}` converges for all `x` where
`0<x<1/2 ` and diverges for all `x` where `x>1/2`.
Note: The ratio test does not
apply when `R=1`. So when `x=1/2` a different analysis must be applied
to the series:
`sum_{k=0}^{oo}{(2 1/2)^k}/{ k+3}= sum_{k=0}^{oo}1/{ k+3}` which
diverges.
[This series is harmonic or use the integal test.]