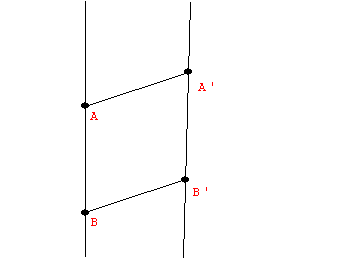
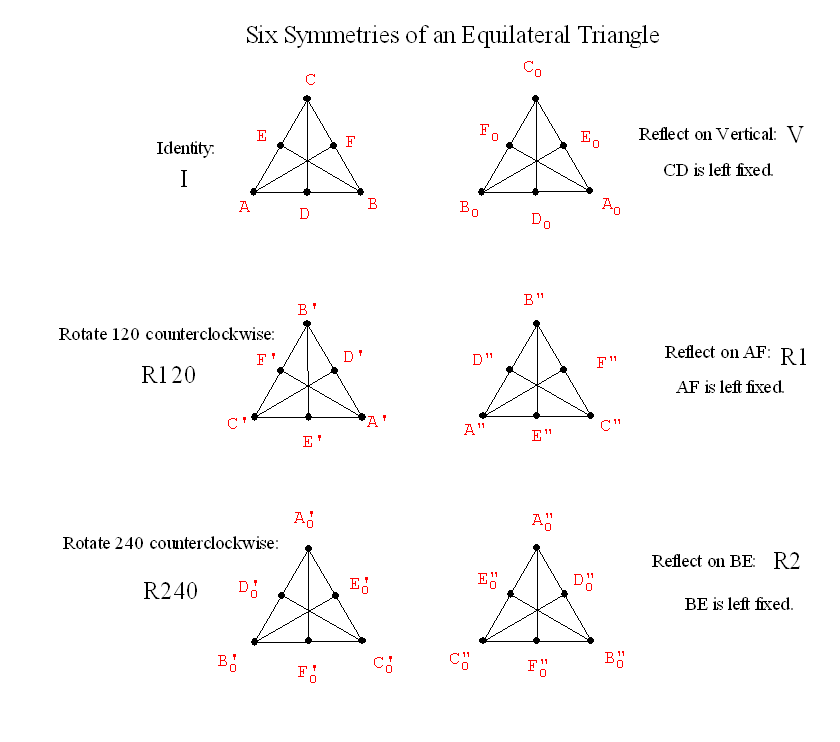
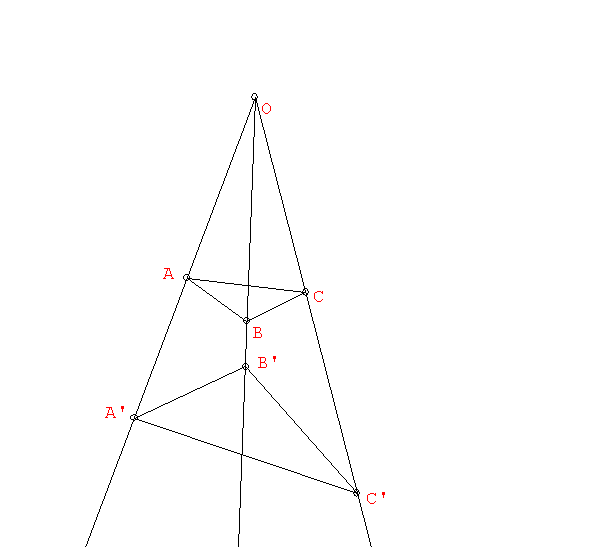
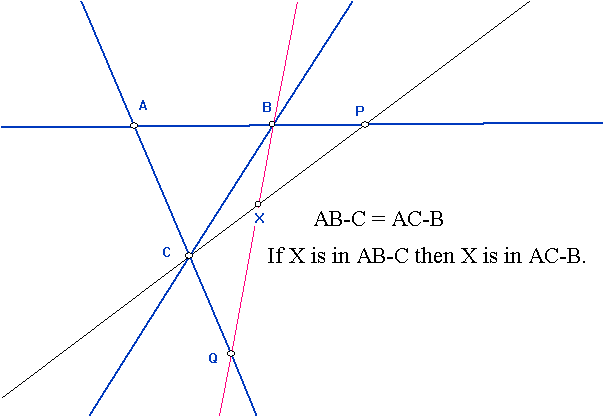
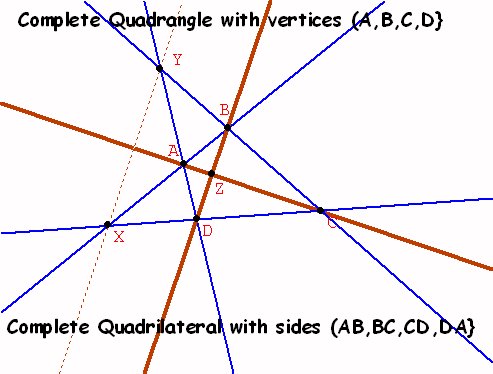
Notice that the figure used to construct P1/2 showed that H(P0 P1,
P¥ P1/2).
Notice that the construction on the affine line of the point P2 from
P0,P1, and P¥ looks
the same.
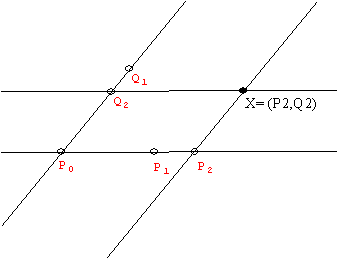
Notice that the figure used to construct P2 shows that H(P1 P¥,
P0 P2).
In general, following this construction of P2, it is possible
to construct a fourth point, D, on a line given A,B and C already on the
line so that H(AB,CD). We can use the construction of P2 to show how
to construct the point D in general. This will be the key to giving a correspondence
between points on a projective line and the real numbers with ¥
as a single additional "number" added to extend the set of numbers.
One key issue then is:
Is the point constructed from the points A,
B and C uniquely determined by the fact that it is in the harmonic relation
with A, B, and C? That is, if A,B, and C are three points
on a line and D and D* are points where H(AB,CD) and H(AB,CD*), then must
D=D*?
This is the question of the uniqueness of the point D. We can prove
that in fact the point D is uniquely determined.
The
proof follows the argument of Meserve and Izzo.
It used Desargues' theorem several times.
Discussion of the dual concept of a harmonic relation between
four lines passing through a single point.
Theorem: If A,B,C, and D are on a line l with H(A,B,C,D)
and O is a point making a section with these four points, consisting of
the four lines a,b,c and d, then H(a,b,c,d).
Proof: see M&I Theorem 5.4.
Corollary: (By Duality) If a,b,c, and d
are on a point O with H(a,b,c,d) and l is a
line making a section with these four lines, consisting of the four points
A,B,C and D, then H(A,B,C,D).
Application:
We can think of a perspectivity between points ABCD on line l
and A'B'C'D' on the line l' with respect to the point O as
being a section of the points ABCD by the point O followed by a section
by the line l' of the lines a,b,c, and d on the point
O.
Applying the previous theorem and its corollary we see that: If
H(AB,CD) then H(ab,cd) and thus H(A'B',C'D').
Note: This application shows that if four harmonically related points
on a line are perspectively related to four points on a second line, then
the second set of four points is also harmonically related. Furthemore,
this result can be extended easily to points that are projectively related.
Thus the transformations of projectivity in projective geometry
preserves the harmonic relationship between four points.
[This last note is comparable to the fact that in Euclidean geometry,
isometries preserve length, and in affine geometry that similarities preserve
proportions.]
Harmonic Conjugate as a Transformation: Given A,B, and C points
on a projective line, we have shown that there is a unique point D so that
H(AB,CD). D is called the harmonic conjugate of C with respect to AB.
In many ways this gives a transformation of the point on the line to
other points that is similar in its nature to reflections and inversions.
Notice that on a projective (affine) line two point will cut the line into
two disjoint pieces, as does a single point for reflection and the points
PR and P-R for inversion, where the transformation
maps points in one set into the other while leaving the "boundary points"
fixed.
With the existence and uniqueness of the point D established, we can
now consider some examples illustrating how to establish a coordinate
system for a projective line by choosing three distinct points to be P0,
P1, and P¥.
We can construct P2, P-1, P1/2, (in two different ways).
Exercise: Construction P3 and P1/3.
Show that with the choice of three points on a projective line
we can construct points using harmonics to correspond to all real numbers
(as in our informal treatment of the affine line).
A brief excursion back to the Inversion Transformation.
Projective transformations of the plane and computers graphics.
The complex numbers, C, and the geometry
of CP(1).
The ordinary points on this "line" can be visualized as
a plane or all the points of a sphere except one- which corresponds to
the north pole or the point at infinity. [Compare this to the visualization
of RP(1) as a circle.]
Algebraic projective transformations of CP(1).
This means first examine what it means for these to be affine, and then
the geometry of addition and multiplication of complex numbers.
Addition
of a constant complex number corresponds to a translation.
Multiplication
by a constant corresponded to a dilation using the absolute value of the
complex number for the factor and a rotation by the angle the corresponding
vector mad with the positive real axis.
An affine transformation
can preserve the distance between complex numbers if |a|=1 where
a is a complex number, so a can be thought of a point on the unit circle
and multiplication by a corresponds to a rotation. So affine transformations
of CP(1) are rotations followed by translations of the plane of
complex numbers.
What about inversions... ?
Review of algebraic projective transformations of the real projective line
RP(1).
RP(1) is characterized using the homogeneous coordinates as a set of
pairs of real numbers <a,b>, not both zero, with <a,b>=<c,d> in
the case there is a nonzero real number t so that c=ta and d=td.
The transformations correspond to 2x2 matrices with non-zero determinant.
These form a group under composition (matrix multiplication) and we have
looked at many examples to see how a matrix transforms points on the projective
line with coordinates to other points on the projective line.
We will see how this transformation is completely determined by the
correspondence of three distinct pairs of points. In some cases the transformation
transforms an ordinary point to an ordinary point, the ideal point to an
ordinary point and an ordinary point to the ideal point, and in some cases
the transformation will transform the ideal point to the ideal point.
A transformation that transforms the ideal point to the ideal point
is called an affine transformation. The composition of two affine transformations
is an affine transformation. The inverse of an affine transformation is
an affine transformation and clearly the identity transformation is an
affine transformation, so the affine transformations are also a group under
the operation of composition (matrix multiplication).
Projective transformations of RP(2) with examples of transformations
previously discussed in the course.
Using homogeneous coordinates of points in the affine plane, we consider
these as points in RP(2). Consider the isometries of translation, rotation,
and reflection of the plane, extended to the affine plane and thus to RP(2).
Translation by <a,b>:
Rotation at (0,0) = <0,0,1>
Reflection about the X- axis:
Reflection about the line Y=X:
Central Similarities at (0,0) by a factor of M.
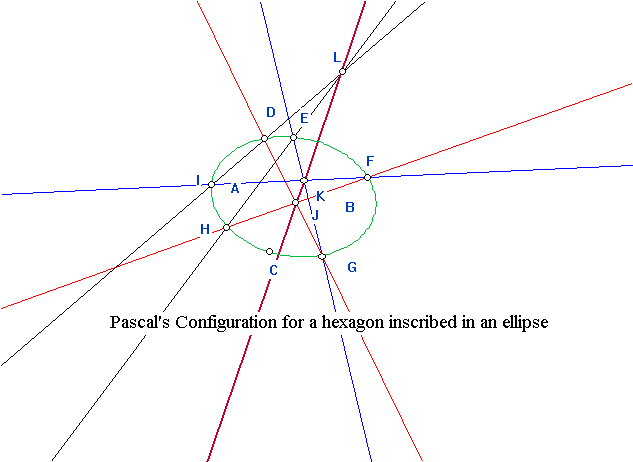
Reconstruction of a point on a conic from Pascal's Theorem.
The following materials are
from previous course notes and have not been incorporated into the current
course notes.
Consider lines connecting corresponding points in a pencil
of points on a line related by a projectivity (not a perspectivity) and
noticed that the envelope of these lines seemed to be a conic, a line
conic. Notice briefly the dual figure which would form a more
traditional point conic. [Also notice how line figures might be related
to solving differential equations e.g. dy/dx=2x-1 with y(0)=3 has a solution
curve determined by the tangent lines determined by the derivative: y=x^2-x+3
which is a parabola.]
In discussing the issue of whether the 5th axiom could be proven
from the other four axioms, we looked at an example of another axiom system,
with an axiom N (any pair of lines having at one point in common)
and an axiom P (given a line l and a point P not on that line there
is a line m where P is on m and m and l have no common points) which is
a version of the parallel postulate (Playfair's - not Euclid's). We gave
examples showing that the four axioms and P were possible as well as the
four axioms and N were possible. This showed that one can not prove axiom
P or N from the other four axioms since P and N are contradictory.
By a similar analysis of the axioms for the seven point geometry
we showed that it not possible prove the 5th postulate from the other four.
The analysis examines the example of the seven point geometry and notices
that by including an 8th and 9th point the resulting geometry would satisfy
the other 4 axioms.
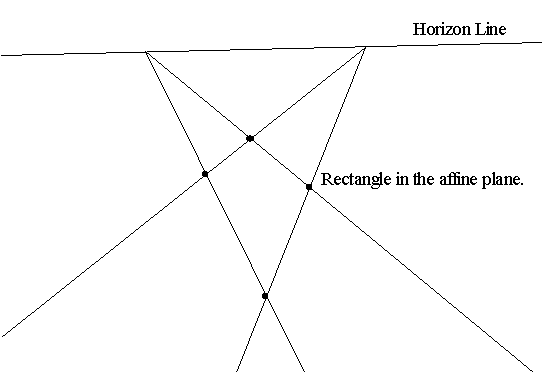
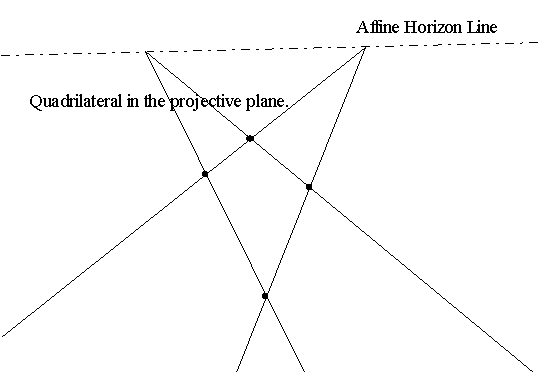
The model we have for affine geometry still satisfies the parallel
postulate, since the ideal (infinite) points of affine geometry are not
considered as ordinary points of the geometry. However, be removing this
distinction between ordinary and ideal points and considering the geometry
that results we obtain a geometry in which there are no parallel lines.
(A projective plane.) This will be a major focus of discussion for the
remainder of the term- especially using the homogeneous coordinates to
consider points in this geometry from an analytic/algebraic approach.
Initial discussion considered the problems of perception and how the
position of an object in a picture can affect our judgment on its relative
size. Turning directly to the question of perspective in drawing we looked
at how an artist tries to capture the visual reality of perception by drawing
figures larger when they are closer to the eye of the beholder. We looked
at some Durer drawings showing some mechanical ways to draw accurate perspective
figures.
An examination of the problems of transferring an spatial image of
a plane to a second plane using the idea of lines of sight we arrived at
an understanding of how points in the plane would correspond to lines through
a point (the eye).
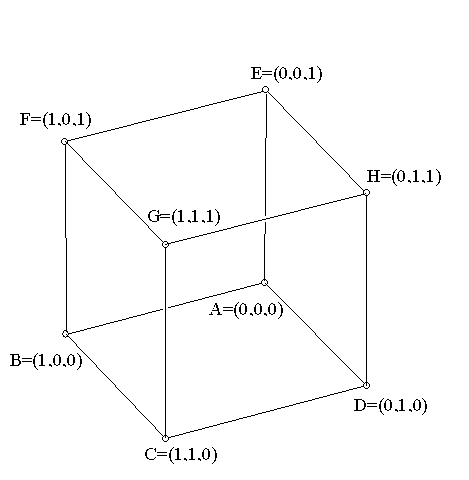
In discussing the 7 point geometry we visualized it using vertices
of a cube (besides (0,0,0)) with their ordinary coordinates in standard
3 dimensional coordinate geometry and identified the 7 points . This allowed
us to identify "lines" using the homogeneous coordinate concepts and their
relation to planes in three dimension through (0,0,0). We identified all
but one of the lines easily- the last plane has ordinary equation X + Y
+ Z = 2... but in this arithmetic for {0,1} we have 1+1=0, so 2=0 and the
vertices of that satisfy this equation in ordinary coordinates {(1,1,0),
(1,0,1),(0,1,1)} form a line as well.
We then discussed using {0,1,2} for homogeneous coordinates connected
to the arithmetic given by the tables
| + |
0 |
1 |
2 |
|
* |
0 |
1 |
2 |
| 0 |
0 |
1 |
2 |
|
0 |
0 |
0 |
0 |
| 1 |
1 |
2 |
0 |
|
1 |
0 |
1 |
2 |
| 2 |
2 |
0 |
1 |
|
2 |
0 |
2 |
1 |
The homogeneous coordinates for this set identify ordered triples, for
example: <1,0,1>=<2,0,2> and <1,0,2>=<2,0,1>. There are
27 possible ordered triples, and thus 26 when we exclude (0,0,0), and these
are each paired by the factor 2 with another triple, so there will be exactly
13 points ( and by the comparable work with lines) and 13 lines in this
geometry.
.... some details still to be reported.
We watched the film on central perspectivities that discussed
perspectivities and projectivities in the plane. Any perspectivity between
a pencil of points on one line and that one another line can be thought
of as a transformation. This transformation is completely determined by
the relation of two pairs of distinct points on two lines. For a projectivity
(the composition of a finite number of perspectivities) the result is that
a projectivity is completely determined by the correspondence of three
points. This result is called the fundamental theorem of projective
geometry and is taken as an axiom by M&I.
[Moved from earlier: The lab time was spent working on sketches showing
ways to understand that result of the CAROMS film about the inscribed triangles
of minimum perimeter.In Lab: Discuss some visual features such as trace
and animation and start to look at the use of coordinates. We'll do more
with coordinates, along with the use of traces and locus to see some aspects
of coordinate geometry next week.]
We also watched the film on projective generation of conics which
introduced Pascal's theorem and its converse about hexagons inscribed in
a conic and showed how to use this result to construct a conic curve passing
through any 5 points. This work was also related to projectivities between
pencils of lines. We will be considering this further in the course. After
a short break we continued using metric ideas to construct an ellipse
as a locus on sketchpad and discussed how to do a parabola as well. By
next Thursday students should construct examples of the three conics on
sketchpad using metric ideas.
Okay... just a quick recall of some of what we covered:
-
Now that we've established how to connect homogeneous coordinates to
a projective line using harmonics we continued by looking at some more
algebraic projective lines- with coefficients of Z2,
Z3,
and
Z5, we saw that these projective lines would have 3,4, and
6 points respectively, corresponding to the 2,3,and 5 ordinary points and
one ideal point. This lead to
-
A discussion of using the complex numbers, C, and the geometry
of CP(1). The ordinary points on this "line" can be visualized as
a plane or all the points of a sphere except one- which corresponds to
the north pole or the point at infinity. [This was compared to the visualization
of RP(1) as a circle.]
-
The discussion turned to algebraic projective transformations of RP(1).
When these leave the ideal point fixed they are called affine transformations
and form a group under composition. We showed that an affine transformation
has a matrix of the form
and therefore T(Px)=Pax+b. Thus an affine transformation of the projective
line is a dilation/reflection followed by a translation.
-
We looked at the idea of establishing the idea of a distance between
ordinary points using absolute value-
d( <a,b>,<c,d>) = |a/b - c/d|. We showed
this is well defined and then discussed what the isometries for this distance
would be. After some analysis we saw that this would mean that in the matrix
of an isometry |a|=1, so a=1 or a=-1. I.e, the matrix is
or that T(Px)=P+/-x+b. Thus an isometry of RP(1) is a reflection followed
by a translation.
-
We also looked further at Pascal's theorem and its planar dual Brianchon's
theorem. Next class we'll prove Brianchon's theorem using an elliptic hyperbaloid.
Today we did more on algebraic projective transformations of CP(1).
This meant first examining what it meant for these to be affine, and then
the geometry of addition and multiplication of complex numbers. Addition
of a constant complex number corresponded to a translation. Multiplication
by a constant corresponded to a dilation using the absolute value of the
complex number for the factor and a rotation by the angle the corresponding
vector mad with the positive real axis. We also saw how affine transformations
could preserve the distance between complex numbers if |a|=1 where
a is a complex number, so a can be thought of a point on the unit circle
and multiplication by a corresponds to a rotation. So affine transformations
of CP(1) are rotations followed by translations of the plane of
complex numbers. Notice these are all orientation preserving transformations.
so any reflection of the plane is not an isometry in this geometry. We
looked briefly at another transformation that was a reflection, namely
complex conjugacy, T(a+bi)=a-bi. This is not an isometry in this geometry
because it is orientation reversing.
We spent the remainder of the lecture time going over the proof of
Brianchon's Theorem using the proof of Hilbert and Cohn-Vossen based on
hexagons lying on the surface of an elliptic hyperbaloid (which is a ruled
surface).