The
Triangulation of Any Polygonal Region
in the Plane
The triangulation of any polygonal region
in the plane is a key element in a proof of the equidecomposable
polygon
theorem.
Proposition: Any region in the plane
bounded by a closed polygon can be decomposed into the union of a
finite number of closed triangular regions which intersect only on the
boundaries.
The proof of this proposition examines a more careful characterization
of the polygonal regions being considered. The key idea of the proof
goes
by induction on the number n = the number vertices = the number of
sides
in the polygon, as follows:
Proof: Consider n = the number vertices =
the number of sides
in the polygon
When n = 3 the result is trivial.
Suppose n> 3 and that for any polygon with k vertices/
sides, where
k<n, the polygon can be triangulated. [An induction hypothesis.]
Now proceed to consider the vertices, v1, v2, ..., vn ordered
so that vi is adjacent to v(i+1) and vn is adjacent to v1.
Take a ray from v1 and rotate it from v1v2 so that it intersects
the inside of the polygon. Continue to rotate until it meets another
vertex.
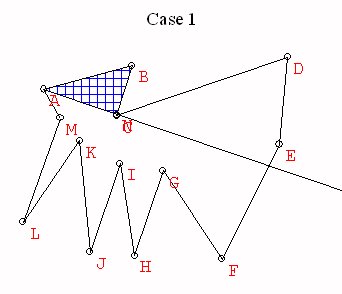
Case 1. This vertex is v3. Then consider
the polygonal region Q1
= v1v3...vn which has n-1 vertices. By induction Q1 can be
triangulated,
so the original polygon is triangulated using the triangulation of Q1
and
the triangle v1v2v3.
Case 2. The vertex is v(n-1). Then consider
the polygonal region Q2
= v1v2v3...vn-1 which has n-1 vertices. By induction Q2 can be
triangulated,
so the original polygon is triangulated using the triangulation of Q2
and
the triangle v1vnv(n-1).
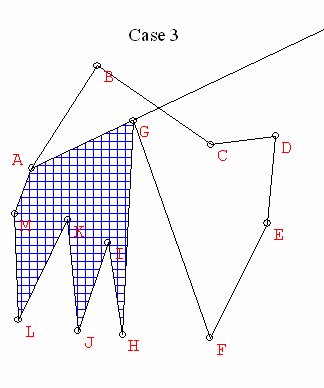
Case 3. The vertex is vk with k different
from 3 or n. Then consider
the polygonal regions Q3 = v1v2...vk which has k vertices (k<n) and
Q4 = v1vkv(k+1)...vn which has n-(k-2)<n vertices. By induction Q3
and
Q4 can be triangulated, so the original polygon is triangulated using
the
triangulations of Q3 and Q4.
This completes the argument that allows the use of induction to
finish the proof of the proposition.
For more discussion of proofs of this proposition see Triangulations
and
arrangements, Two lectures by Godfried Toussaint, transcribed by
Laura Anderson and Peter Yamamoto.