An example of vector methods in geometry:
Proposition: The perpendicular bisectors of any triangle meet in a single point [which is equidistant from the vertices]

Proof: Suppose the triangle has vertices A, B , and C. Let v, w and z be the vectors corrsponding to the vectors AB, AC, and BC, so that v = AB, w = AC and  z = BC; and  w = v + z.
Let N, M, and P be the midpoints of AB, AC and BC respectively. Suppose the perpendicular bisectors of AB and AC meet at the point O. Let m  denote the vector MO and n   denote the vector NO. It suffices to show that the vector p = OP is perpendicular to the vector z.

From the vector definitions it should be clear that z = w -v, while
1/2 v + n = 1/2 w + m = v + 1/2 z - p

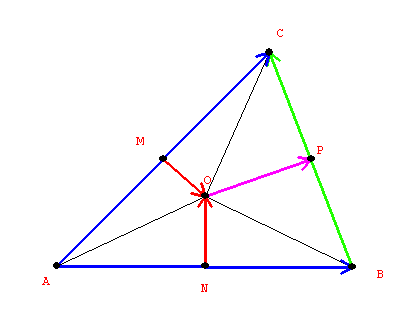
To show p is perpendicular to z it is enough to show that the inner (dot) product of p z = 0.
Now p = v +1/2 z - 1/2 v - n = 1/2 v + 1/2 (w-v)  - n = 1/2 w - n  , so
p z = (1/2 w   - n) (w - v) = 1/2 w w - wn - 1/2 w v  + n v.  But since n is perpendicular to AB,
nv = 0 so  we have
p z = 1/2 ww - wn - 1/2 v w =w (1/2  w - n - 1/2 v)
= w  ( 1/2 w  - (1/2 v + n)) =w  ( 1/2 w  - (1/2 w + m))= w (-m) = 0    
because  m   is perpendicular to AC.

From the geometry is is clear that the point O must be equidistant from A, B, C and thus is the center of the circle that passes through the points A, B, and C, - the circumcenter of the triangle ABC.