Scissors Congruent Polygons

SCISSORS CONGRUENT (EQUIDECOMPOSABLE) POLYGONS

DEFINITION: Two figures, F and G, are Scissors Congruent if one can be cut into polygonal pieces which can be rearranged to form the other.
When F is S.Congruent to G we'll write F SC= G .

I. Basic Facts about S. Congruence.
A. If F SC= G then F and G have the same area.
B. (i) F SC= F. (REFLEXIVITY)
(ii) If F SC= G then G SC= F. (SYMMETRY)
(iii) If F SC= G and G SC= H then F SC= H. (TRANSITIVITY)

II. Parallelograms.
A. (Euclid) Two parallelograms with the same base between the same parallels have the same area. Proposition 35.Proposition 36.
B. Two parallelograms with the same base and the same area are S. Congruent.
C. Two parallelograms of the same area are S. Congruent.
D. Given two parallelograms P and Q, one can form a third parallelogram R which is S. Congruent to their disjoint union.

III. Triangles and Polygons.
A. (Euclid) Any triangle is S. Congruent to a parallelogram
.

Proof: The midpoint proposition.
The line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is congruent to one half of the third side.

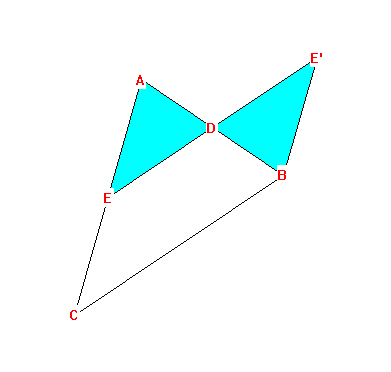
By rotating the small triangle created by connecting the midpoints of two sides of a triangle 180 degrees about one of the midpoints, we obtain a parallelogram.
This shows that the triangle's area is the area of this parallelogram which can be computed by using the length of the base of the triangle and 1/2 of its altitude- which is the altitude of the parallelogram.

B. Any polygon can be decomposed into triangles.

THEOREM: Any two polygons F and G of equal area are S. Congruent.
Proof ( and Procedure ):

1. Decompose both polygons into triangles. (III B.)
F - - S₁, S₂,..., S_k
G - - T₁, T₂,..., T_k

2. Each triangle is S. Congruent to a parallelogram. (III A.)
S₁ SC= P₁, S₂ SC= P₂,..., S_k SC= P_k
T₁ SC= Q₁, T₂ SC= Q₂,..., T_k SC= Q_k

3. Each polygon is S.Congruent to a parallelogram . (II D.)
F SC= P , G SC= Q .

4. These parallelograms have equal area, hence they are S.Congruent.
P SC= Q (II C.)

5. F SC= G (I B.)

Notes:

The analogous problem in three dimensional geometry: volume equality of polyhedra is a necessary but not sufficient condition for a similar result. This was the third of the famous 23 "Hilbert problems" for the 20th century. This was first demonstrated by Dehn in the 1930's by using another invariant of polyhedra related to the lengths of the edges and the dihedral angles between the faces of the polyhedra. References to be supplied.