An Appplication of Conjugation
Notes for Math 371 by M. Flashman
Consider the
isometry of the coordinate plane that is rotation by 90 degrees
counterclockwise about the point (1,2). We will call this
transformation T.
We denote
by L ... the translation of the plane by the vector <-1,-2> ,
by T'... the rotation of the plane by 90 degrees about the origin (0,0), and
by L-1 ... the translation of the plane by the vector <1,2>.
Then T = L-1T'L as a transformation.
So
Here is the visualization of T as a map in Winplot using: (x,y)==>(3-y,x+1)
We denote
by L ... the translation of the plane by the vector <-1,-2> ,
by T'... the rotation of the plane by 90 degrees about the origin (0,0), and
by L-1 ... the translation of the plane by the vector <1,2>.
Then T = L-1T'L as a transformation.
So
| L[ |
x |
]=[ | x-1 |
]=[ | x' |
] |
| y |
y-2 |
y' | ||||
| T'[ | x' |
]=[ | -y' |
] | ||
| y' | x' |
|||||
| L-1[ | -y' |
]=[ | -y' +1 |
]=[ | -(y-2)+1 | ] |
| x |
x' +2 |
x -1 +2 |
||||
| and thus we have |
||||||
| T[ | x |
]=[ | 3-y |
] | ||
| y |
x+1 |
|||||
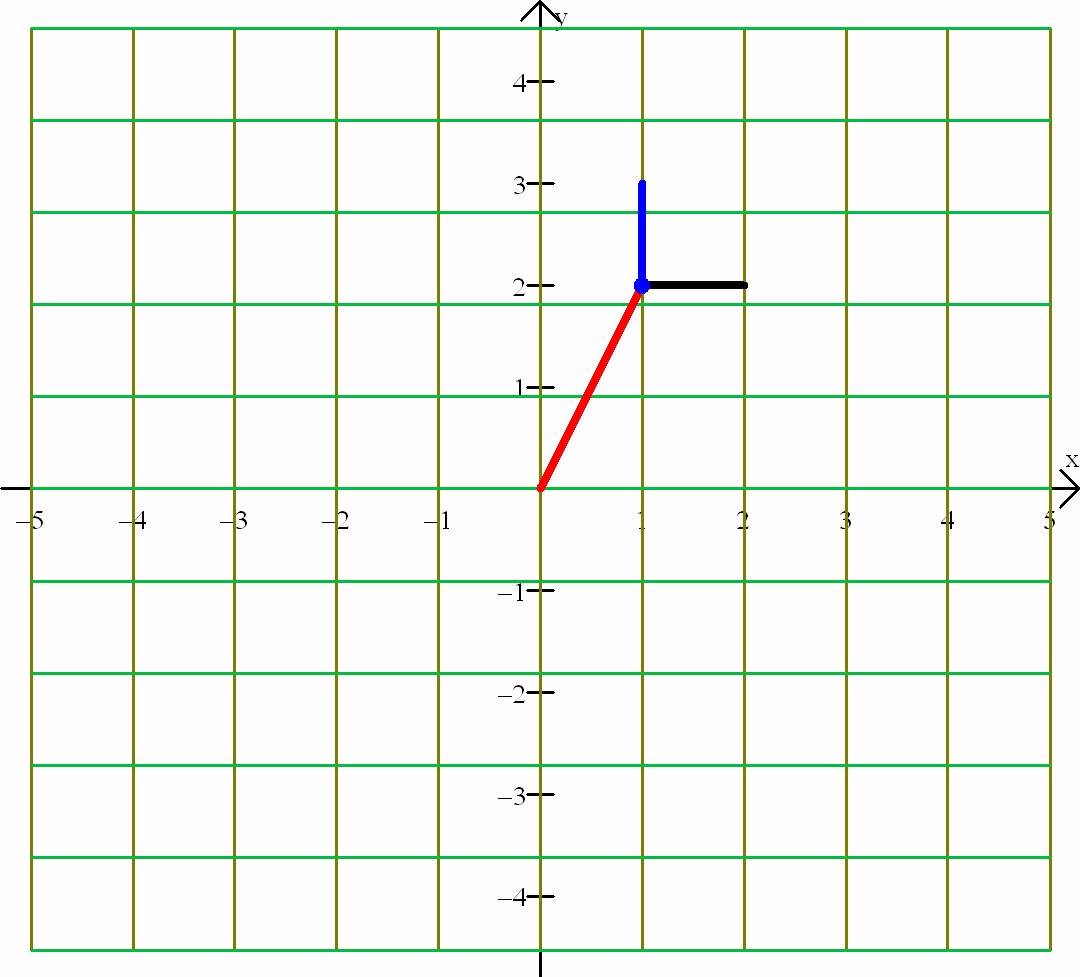
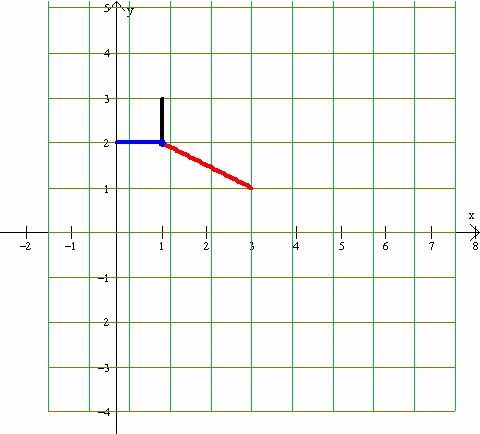
Here is the visualization of T as a map in Winplot using: (x,y)==>(3-y,x+1)
 |
 |
| Plane before the Application of T |
Plane after the Application of T |