| Tuesday | Thursday | ||||||
|
Introduction to "Visual Math" |
The Pythagorean Theorem 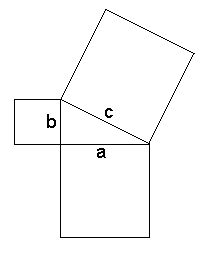 a2 + b2 = c2 |
||||||
| 9-2
Tangrams and Dissection Puzzles  |
9-4
Dissection Puzzles & Scissors Congruent (Equidecomposable) Polygons
|
||||||
|
Dissection Theorem for Regular Polygons BeginTilings of the Plane 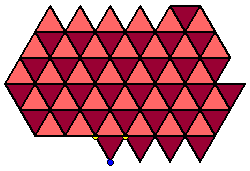 |
Regular and Semi- regular Tilings of the Plane  |
||||||
| 9-16 Symmetries for a Single Polygon Reflections and Rotations 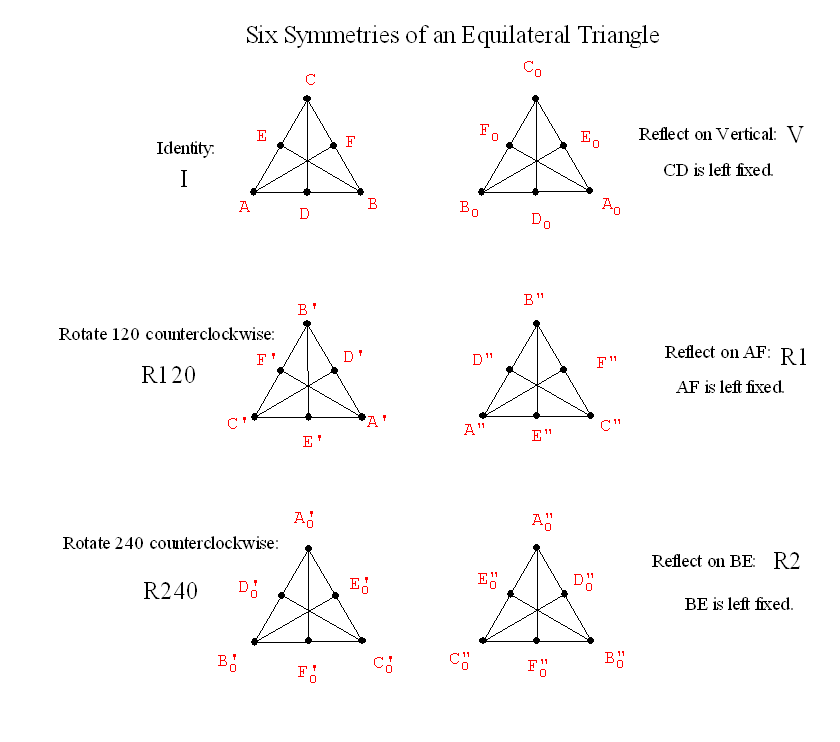 |
9-18 Symmetries for a Frieze Pattern on a Strip Translations and Glide Reflections ...|p|q|p|q|p|q|p|q|p|q|p|... ...|d|b|d|b|d|b|d|b|d|b|d|... |
||||||
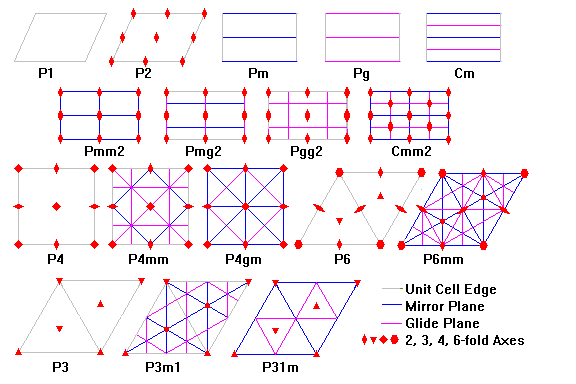 |
9-25 Isometries in Symmetry Groups and planar tilings. Begin Space- Symmetries and Isometries Rotations and Reflections  |
||||||
|
10-2 Spatial Symmetry The Platonic and Archimedean Solids.
|
||||||
| 10-7 More on Solids. Connections between Polyhedra. Frameworks. Duality.
|
10-9 Similarity in the plane and space. 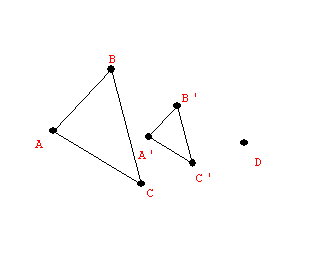 |
||||||
| 10-14 Geometric Sequences, Series and Space Filling Curves
|
10-16 Space Filling Curves and The Hypercube. 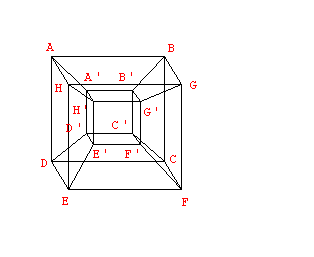 |
||||||
| 10-21 More Encounters with The Fourth Dimension  |
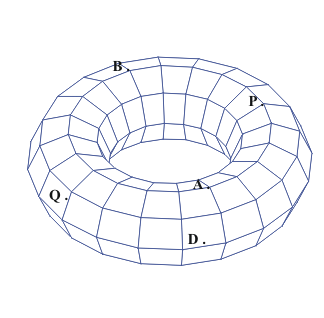
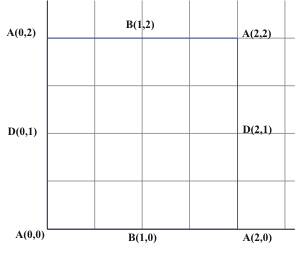
10-23 What about higher dimensions? Maps and Coordinates for Surfaces: Flatland, The Earth and The Torus.
|
||||||
 |
10-30 Perspective and Projective Geometry 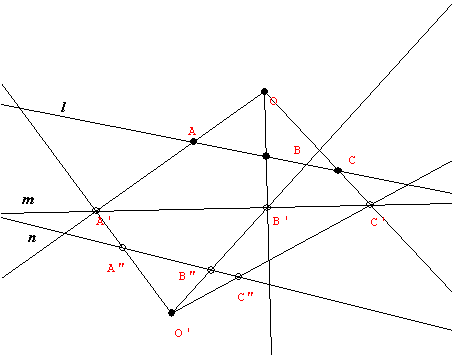 |
||||||
| 11-4 Perspective in Space and The Projective Plane 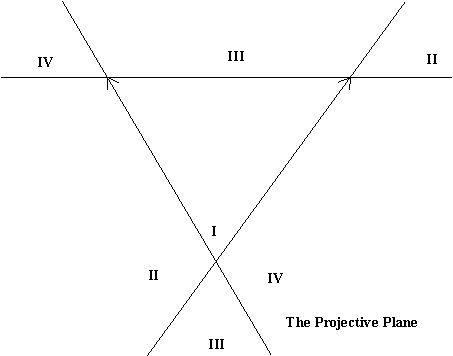 |
11-6 The Cone and The Conic Sections 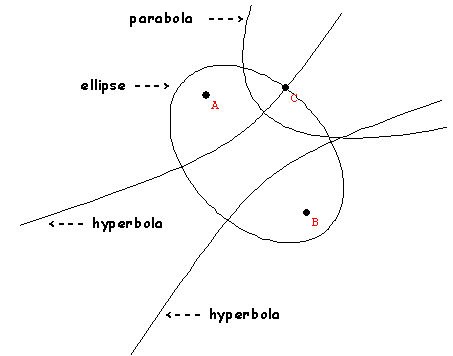 |
||||||
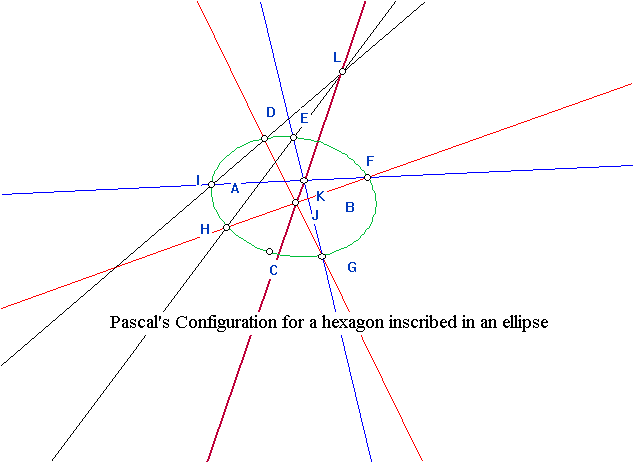
| 11-11 Projective Geometry: An Introduction to Desargues' Theorem 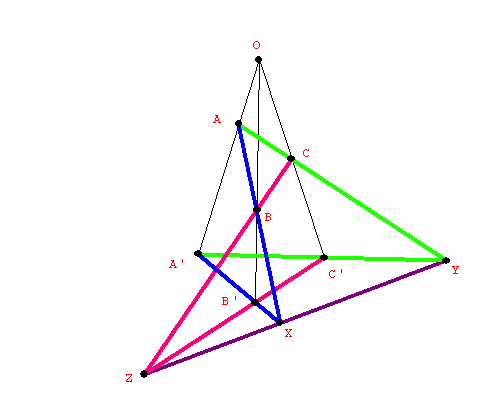 |
|||||||
| 11-18 More Duality and Proofs. What is possible and what is not! Properties of Curves and Surfaces: Geometric, projective, and topological. 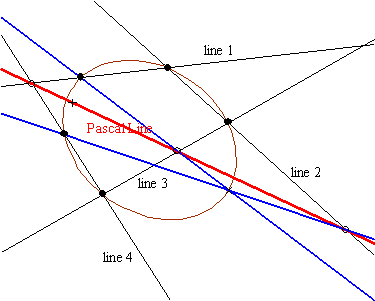 |
V+R = E + 2
|
||||||
|
Appplications of the Euler Formula and a "Hard Problem":
What's possible and what's impossible! The Color Problems on the plane, the sphere, and the torus... 
|
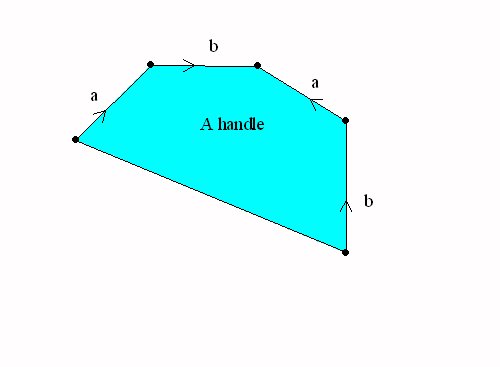
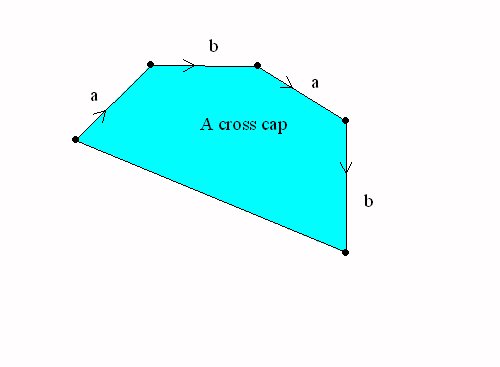
Other Worlds and Surfaces:
A Non-euclidean Universe. New adventures on the Mobius Band, the Klein Bottle, and the Projective Plane. 


|
||||||
|
|
12-11 Turning a sphere inside out.
Some Last Remarks and Videos on Flatland and Visual Mathematics Project Fair |