The Sum of A Geometric Series of Lengths.
© 2000 M.
Flashman
We consider a sequence of lengths where the ratio of each length
to the previous length is a constant.
Examples:
- If the ratio is 1/2 and the first length has a measurement of
4, then the sequence is 4,2,1,1/2,1/4,1/8,1/16,...
- If the ratio is 1/5 and the first length has a measurement of 25,
then the sequence is 25,5,1,1/5,1/25,1/125,1/625,...
- If the ratio is 2/3 and the first length has a measurement of
9, then the sequence is 9,6,4,8/3,16/9,32/27,64/81,128/243,...
- If the ratio is 4 and the
first length has a measurement of 3, then the sequence is
3,12,48,152,...
- If the ratio is 4/3 and the first length has a measurement of 3,
then the sequence is 3, 4, 16/3, 64/9, 256/27, 1024/81,...
- If the ratio is r and the first length has a measurement of 1,
then the sequence is 1, r, r2, r3, r4,
r5,...
A sequence of this type is called a geometric
sequence.
Suppose we add the terms of a geometric sequence:
Example: 4 + 2+1 + 1/2 +1/4 + 1/8 +... = 7 + "1" = 8
BUT ... what about the other sequences?
Consider the general sequence 1, r, r2,
r3, r4, r5,... and the sum of the
first n terms,
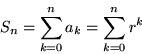
.
Then
for any r where 0<r<1 and a large value of n, S
n is close to 1/(1-r).
Here is a visual argument to justify the previous statement:
In the figure below, consider the left most square to have side
of length
1.
There are several similar squares with the ratios of the sides being
r/1 in the figure where 0<r<1.
Using the large right triangle with base AB and the similar right
triangle cut at the top of the left most square notice that
AB/1 =
1/(1-r).
But the sides of n of these squares accumulate to
give a length of S
n , and when n is large, this sum is very
close to
AB = 1/(1-r).
Application to Economics:
The
multiplier effect
In studying the economics of the United States ( or any large economic
entity) we are interested in determining the total amount of money
spent on purchasing goods and services in a single year. This
amount of money is called the gross domestic product.
Suppose that whenever an individual receives money he or she spends 80%
of the money on goods and services and puts the remaining 20% into a
bank where the money is essentially removed from circulation for
purchasing goods and services.
Assume that any money spent on goods and
services is paid to an individual either as salary or earnings.
The
issue is what is the effect of adding an additional one million
(or one billion) dollars as purchases to the GDP.
Since 80% of
that initial amount will be spent on purchases that will be added to
the GNP, we have 1 +.8 added to the GDP, but the process continues, so
that after several repeated purchase we have 1 + .8 + (.8) (.8) +.... +
(.8) 20 dollars added to the GDP.
But we have just shown that this sum,
1 + .8 + (.8) (.8) +.... +
(.8) 20 is approximately
1/(1-.8) = 1/.2 = 5.
So the result of initial
purchases of one million dollars will be about 5 million dollars change
in the GDP.
Alternative plan:
Suppose instead of adding one million dollars through purchases
to the economy, the money is given to individuals as a gift- such as
a tax cut or rebate. Then the original one million dollars is not
counted in the GDP and the resulting effect on the GDP will be .8
+ (.8) (.8) +.... + (.8)^ 20 dollars which is 1 million dollars less in
total or only 4 million dollars in additional GDP.
Thus we can see that the effect of government action can have more or
less effect on the GDP - if the government spends the money in
purchasing goods or services rather than giving a tax rebate or cut,
the GDP will increased by one million dollars more .
This is a major
part of the (Keynesian) economic argument that the
larger increase in the GDP (which will result in more jobs) is through government
spending, not tax cuts.
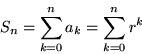 .
.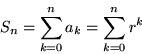 .
.