Tuesday, November 11
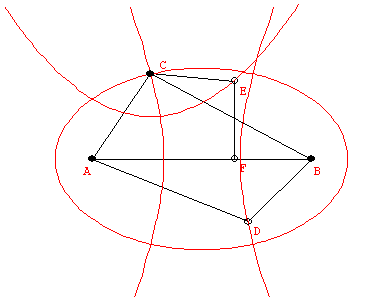
Last class we saw the conics from cross sections on a cone and the characterization of points on a conic by measurements:
ellipse: AC + BC = constant
parabola: EC = EF
hyperbola: |CB-CA| = constant.
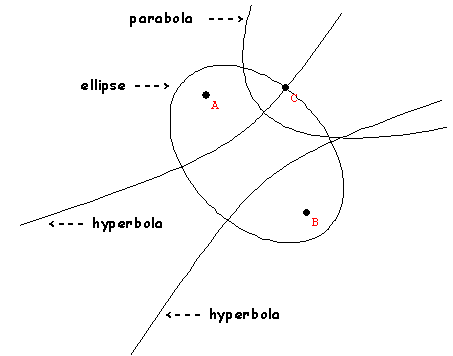
The Conics Video shows how the conics are connected to these measurement qualities.
Key background: Tangents to a circle are equal in length.
In right triangle, the ratios of the length of the side opposite an angle to the hypotenuse length depends only on the angle. This ratio is called the sine of the angle and is abbreviated "sin".
If the angle is designated by the vertex A in a right triangle ABC where the right angle is at vertex C, then sin(A) = BC/AB.
Example: If A is a 45 degree angle, sin(A) = 1/ sqrt(2).
If A is a 30 degree angle, sin(A) = 1/2.
Show "Conics" video
Equations for conics in coordinate geometry.
Using coordinates to draw in perspective.
Activity: Creating coordinates in the projective plane and using them
to transfer a circle to the projective plane as an ellipse.
What do the conics look like in a perspective drawing or in the projective plane?
Projective geometry: The study of properties of figures that are related by projections... perspectivities and projectivities.
Examples: The projection of a line is a line. The point of intersection
of two lines will project to the point of intersection of the projected
lines.
Desargues' Theorem in Space: