Martin Flashman's Courses - Math 371 Spring, '16
Geometry Notes
Geometric Structures for the Visual
[Work in Progress DRAFT VERSION Based on
notes from 09 and 11]
Notes on Java and JavaSketchpad Malfunction:
The use of Java has become a browser and machine dependent issue.
In particular, the Java used in David Joyce's version of Euclid does not
work uniformly in Firefox on HSU computers, but does seem to work on
Chrome. Other Java works in Firefox, but not in Chrome. I will try to
indicate these dependencies when possible.
Readers who might have difficulty running the Java applets
are advised to use a book marklet that converts JavaSketchpad sketches
on this page (or anywhere else on the internet) to work completely
independently of Java.
Go to this site
http://dn.kcptech.com/builds/804.12-r/cdn/bookmarklet.html
to install the small tool in your web browser
OR
click on the following link to "fix" the java.
Convert JavaSketch
Please give feedback,
whether bug reports or other, at the following email address:
wsp@kcptech.com
Blue
sections indicate
tentative plans for those dates.
Week
|
Monday
|
Wednesday
|
Friday
|
1
|
|
1-20 Introduction
|
1-22 Continue discussion of what
is "geometry"?
Start on Euclid- Definitions, Postulates, and Prop 1.
|
2
|
1-25 Euclid- Definitions, Postulates,
and Prop 1. cont'd
|
1-27 Pythagorean plus.
|
1-29 Euclid Postulates/ Pythagoras
|
3
|
2-1 Euclid early Props/ Pythagoras/
Dissections?-
equidecomposeable polygon . |
2-3Begin Constructions and the real number line
M&I's Euclidean Geometry
|
2-5 More on Equidecomposeable polygons
|
4
|
2-8
|
2-10
|
2-12
|
5
|
2-15
|
2-17
|
2-19
|
6
|
2-22
|
2-24
|
2-26
|
7
|
2-29
|
3-2
|
3-4
|
8
|
3-7
|
3-9
|
3-11
|
9
|
3-14 No class Spring Break!
|
3-16 No
class
Spring
Break! |
3-18 No class Spring Break!
|
10
|
3-21
|
3-23
|
3-25
|
11
|
3-28
|
3-30
|
4-1
|
12
|
4-4
|
4-6
|
4-8
|
13
|
4-11
|
4-13
|
|
14
|
4-18 |
4-20
|
4-22
|
15
|
4-25
|
4- 27
|
4-29
|
16
|
5-2
|
5-4 |
|
- 1-20/22 Introductory Classes Summary (+).
What are different aspects of geometry? How is the study of geometry
organized? Analytic(numbers) , Synthetic(axiomatic),
Transformations (functions) are three ways to organize information and
the study of geometry. Also Projective and Differential geometry were
mentioned as alternative focuses for studying geometry.
- Additional Relevant Notes:
- Different types of geometry:
- Euclidean: Lengths are important
- Similarity: Shape is important
- Affine: Parallel lines are important.
- Projective: "Shadows" are important
- Differential: Curvature is important.
- Topological: General shape- especially holes and connectedness-
is important.
- What is synthetic geometry? A geometry that focuses on connecting
statements
(theorems, constructions) to a foundation of "axioms" by using proofs.
- What is analytic geometry? A geometry that focuses on connecting
statements
(theorems, constructions) to a foundation of number based algebra.
- What is "structural geometry"? A geometry that focuses on
connecting statements
(theorems, constructions) to a foundation of structures (relations and
operations) on sets by using proofs.
- transformations: tools that allow for changing figures:[the basis for studying different geometries in the Klein Erlangen Program. See Felix Klein - YouTube Felix Klein (25 April 1849 – 22 June 1925)
- Euclidean: translations,
rotations, and reflections.
- Similarity: magnifications, dilations
- Affine: Preserve parallel lines
- Projective: "linear projections"...line preserving
- Differential: "smooth".
- Topology: continuous
1-25 Still to be covered is the course project on the assignments webpage.
-
geometry as an empirical science
- geometry as a formal system of information
- geometry focused on special objects like triangles, or special
qualities
like convexity.
- Geometry
on
the
web and using GeoGebra
- Geometry has traditionally been interested in both results-
like
the
Pythagorean
Theorem- and foundations - using
axioms
to justify the result in some rigorous organization. We will be
concerned
with both results and foundations.
- We will attempt to build an understanding of both the synthetic
and analytic approaches to geometry by using the tools of a structural
approach.
- In the distinction between
synthetic and analytic geometry the key connecting
concept is the use of measurements.
- Initially we will try to avoid when
possible the
use of measurement based concepts in the structures we use .
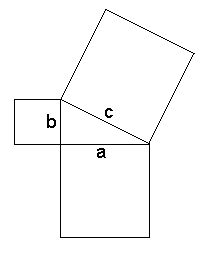
In one alternative proof for this theorem illustrated in the GeoGebra
sketch
below, follow the movie to consider 4 congruent right triangles and the square on the side of the hypotenuse arranged
inside of a square with side "b+c" and then
moving through the movie the
same 4 triangles and 2 squares arranged
inside of a square with side "b+c" . Can you explain how this
sketch
justifies the theorem?
1-27 Review of previous "proof of the PT.
- Consider the on-line version of Euclid's
Geometry- especially Book
1:
- The list (on-line) of initial definitions and
postulates. ( We will continue a discussion of these in more detail
later in the course.) The end results of Book I are The Pythagorean
Theorem and
its converse.
- Consider Proposition 1 and that statement appear justified by the definitions and postulates! A more detailed
discussion of this proposition is found below.
- Discuss: What would
we need in geometry to make a proof of the PT based on this activity?
- What kind of structures and assumptions were
needed in the proof with the 4 triangles and squares?
Here are some considerations related to those assumptions:
- What types of objects are being considered?
- points
- lines
- line segments
- angles
- triangles
- squares
- What types of relations are being considered?
- points on lines
- Lines intersecting at points
- Congruent line segments
- congruent angles
- congruent figures (triangles, squares)
- Decomposing and recomposing a figure.
- How could we justify identifying "equal" objects
(congruent figures)?
- How do the objects fit together?
- How do movements effect the shapes of objects.
Consider the Pythagorean
Theorem
Activity
Sheet.
- Back to Euclid for some further examination of the postulates:
- Looking at the definitions and postulates, a key feature of
any geometric structure appears early- What defines a point and
a line?
- An alternative- minimal geometry: points: A,B.
lines: {A,B}. That's all!
- Postulate 1. To draw a straight line
from any point to any point.
- Current
view: Two distinct points determine a unique straight line.
- Issue: What
is a "straight" line?
- Alternative
geometry- spherical. Points: points on a unit sphere in coordinate
space: { (x,y,z): x2 + y2
+ z2=1}
Straight lines: Great Circles on the sphere. Determined by a
plane in space through (0,0,0).
Fact: Two points on the sphere that are not antipodal- (Opposite)
determine a unique straight line. [Use the plane determined by the two
points and (0,0,0).] For this to make this spherical geometry satisfy
Post 1- redefine what "distinct" means: If the points on the unit
sphere are antipodal, then they are considered "equal" and thus not
distinct.
1-29:
- Postulate 2. To produce a finite straight line continuously in a
straight line.
- Current view:
A straight line has no "endpoints".
- Issue: What
is the nature of a straight line not being "finite"?
Alternative Geometry. Points: all numbers in an open interval {x:
0<x<1}. Straight line: The interval (0,1) and all subintervals.
A "finite" straight line: Any closed sub-interval of (0,1).
Fact: Any closed sub-interval of (0,1) is properly contained in another
closed subinterval of (0,1).
Proof: Suppose 0<a,b<1. Then [a,b] is contained in the interval
`[a/2, (b+1)/2]` which is contained in (0,1).
- Postulate 5. That, if a straight
line falling on two straight lines makes the interior angles on the
same side less than two right angles, the two straight lines, if
produced indefinitely, meet on that side on which are the angles less
than the two right angles.
- Current view:
Under the given circumstances, the two straight lines are not
parallel.
Issue: How can you find the actual point
where the lines meet?
Here is the most distinctive of the postulates that appear in Euclid.
The definition
of parallel: Parallel straight lines are straight
lines which, being in the same plane and being produced indefinitely
in both directions, do not meet one another in either direction.
- Looking at "Common Notions" we see the geometry has
language for equality and addition- a relation and an operation for the
objects.
- 2-1
- Look at how the definitions and postulates are used in
Euclid:
- These propositions demonstrate that Euclid did not treat
moving a line
segment as an essential property worthy of being at the foundations as
an axiom. However, this is a fundamental tool for all of geometry.
- Note that in the proof of proposition 1 the point of
intersection
of circles is presumed to exist without reference to any of the
postulates.
This presumptions was left implicit for hundreds of years, but were
cleared
up in the late 19th century (see the work of David Hilbert) when
careful attention was given again to the axioms
as a whole system.
- Notes on Existence:
Existence is an often
overlooked quality in a mathematical statement:
For example it is common to state that `sqrt{2}`
is an irrational number.
The proof starts by assuming `sqrt{2}` is a rational
number, say `sqrt{2} = p/q` where `p` and `q` are natural numbers, so
that
... `2 q^2 = p^2`. From this the usual proof
of
the statement deduces a contradiction. However, the statement
assumes
that there is a number the square of which is equal to `2`.
One can justify the existence of the square root
of `2` in many ways. One way presumes that any line segment has a length
measured by a real number. Then by the Pythagorean theorem, the
diagonal
of a unit square will have length `sqrt{2}`.
- Alternative "rational
coordinate" plane geometry. [A geometry in which circles do not always
intersect.]
Points: ordered pairs of rational
numbers.
An example of a point not in the rational
coordinate plane is the point `(sqrt{2},0)`. This point can be
constructed
in the ordinary plane with straight edge and compass using the circle
with
center `(0,0)` and radius determined by the points `(0,0)` and `(1,1)`. This
circle will meet the X-coordinate axis at the point `(sqrt{2},0)`
The circle with center `(0,0)` and radius `1` and
the circle with center `(1,0)` and radius `1` meet in the ordinary plane at
the points with coordinates `(1/2, sqrt{3}/2)` and `(1/2, -sqrt{3}/2)` .
Since `sqrt{3}/2`
is not a rational number, this ordered pair does not correspond to a
point
in the rational coordinate plane, so the two circles do not have a
point
of intersection in the rational coordinate plane.
- Note: Proposition 1 has a statement that was
not justified by the definitions and postulates!
- Proposition 2 demonstrates a concern of Euclid about
establishing a "motion" or transformation for this geometry based on
fundamental postulates.
- An example of the "web" of information formed in this
"axiomatic" synthetic geometry.
- Not
just demonstrations- but the first two propositions are dedicated to
constructions! A focus on existence as well as conditions that
guarantee other conditions.
2-3 Some Comments on Problem Set #1:Intersections for families of convex figures:
Using the notation of M & I:
`cap \{ [P_0P_r : r>0\} = \{P_0\} ; cap \{
[P_{-1-r}P_{1+r} : r>0\} = \{P_{-1}P_1\}`
To show that `\D = `{`P` in plane where
`d(P,P^*) le 1`} is convex where `P^*` is a point in the plane,
recognize that `D = cap` { half
planes determined by tangent lines to the boundary of `D` that contain
`P^*`}. These half planes are all convex.
[Side Trip?] Moving line segments: Can we move a line segment without changing its length.
We can look further at the foundations of the
proofs of the Pythagorean Theorem in two ways:
1. Dissections:
How
are
figures
cut and pasted together? Can be the proof be achieved using
dissections?
Solution!
- Cutting and
reassembling polygons. More ....
- Dissections
(like Tangrams)
and equidecomposable
polygons.
- Use tangram pieces to make a square.
- Note that in putting the pieces together to form any other
shape,
the area of that shape would be the same as the area of the square
unless
there is some overlap of the pieces in the shape.
- Question: Is this necessary condition of equal areas
sufficient
to say that two polygonal regions could be decomposed (cut and pasted)
into smaller regions that would be congruent?
Comment: In a sense a positive (yes) response to this question means
that one could create a set of smaller shapes with which one could make
either of the two regions using precisely these smaller shapes. The
answer
to this question is yes (in fact this is a late 19th - early 20th
century result), which
is the basis for the remainder of this section
[The analogous problem in three dimensional geometry: volume equality
of polyhedra is a necessary but not sufficient condition for a similar
result. This was the third of the famous
23 "Hilbert problems" for the 20th century. This was first
demonstrated
by Dehn almost as soon as the problem was announced. Dehn used another
invariant of polyhedra related to
the lengths of the edges and the dihedral angles between the faces of
the
polyhedra.[
"Ueber den Rauminhalt," Math. Annalen, 55 (1902), 465-478].
See also A New Approach to Hilbert's Third Problem - University of ...by D Benko.
First, consider some of the background results which were known to
Euclid:
(1) parallelograms results and (2) triangle results. The justifications
for these results can be reviewed briefly.
(1) a. Parallelograms between a pair of parallel lines and on the
same
line segment are equal (in the sense of being able to decompose one to
reconstruct the other). Proposition
35.
b. Parallelograms between a pair of parallel lines and on
congruent
segments are equal (in the sense of being able to decompose one to
reconstruct
the other). Proposition
36.
(2) a. The line segment connecting the midpoints of two
sides
of a triangle is parallel to the third side and is congruent to one
half
of the third side.
[The justification of this result is left
as an exercise in traditional Euclidean Geometry.]
b. By rotating the small triangle created by connecting the midpoints
of two sides of a triangle 180 degrees about one of the midpoints, we
obtain
a parallelogram. (This shows that the triangle's area is the area
of this parallelogram which can be computed by using the length of the
base of the triangle and 1/2 of its altitude- which is the altitude of
the parallelogram.)
Compare this with Euclid
Prop. 42 and Prop. 44.
(ii) The triangulation of any polygonal region
in the plane is a key element in a proof of the equidecomposable
polygon
theorem.
The proof of this proposition examines a more careful
characterization
of the polygonal regions being considered. The key idea of the proof
goes
by induction on the number n = the number vertices = the number of
sides
in the polygon. Proof of the
triangulation proposition.
Another component of the proof of the equidecomposable polygon
theorem is the ability to "add two parallelograms to form a single
parallelogram which
is scissors congruent to the two separate parallelograms". Here's how:
Intersect two pairs of parallel lines, l and l' with m and m'- one
from each of the given parallelograms. Draw a diagonal HI in the
resulting
parallelogram.
Cut and translate one parallelogram so that it is scissors congruent
to a parallelogram HIJK within the same parallel lines l and l' with
one
side being the diagonal.
Cut and translate the other parallelogram so that it is scissors
congruent
to a parallelogram HINO within the same parallel lines m and m' with
one
side being the diagonal and on the other side of the diagonal HI from
the
transformed first parallelogram. Now draw the parallel NO to the
diagonal
in the second transformed parallelogram HINO so that it intersects the
parallels l and l' from the first parallelogram at the points P
and
Q. This makes one larger parallelogram JKPQ which is scissors congruent
to the original two parallelograms.
Compare this with Euclid
Proposition
45.
Follow this link for a proof of the equidecomposable
polygon theorem. or here is a
slightly
different
approach.
The film Equidecomposable Polygons also proves the result:
If two polygonal regions in the plane have the same area, then
there
is a decomposition of each into polygons so that these smaller polygons
can be moved individually between the two polygons by translations or
half
turns (rotations by 180 degrees).
Read the definitions in M&I
section 1.1
REVIEW of basic plane geometry
concepts and definitions based on M&I.
M&I build their foundations for Euclidean geometry on a one to
one correspondence between points on a line and real numbers and the
ability
to match angles with numbers between 0 and 180.
Review materials defining rays, segments, angles, triangles,
and planes in M&I.
These definitions present a model for geometry based on the real
numbers. Points, rays, line segments, etc., are identified with real
numbers and intervals of real numbers. Notice that angles in the plane
are not oriented and are always considered to have a measure
between 0 and 180.
Review eight of the basic Euclidean
constructions
described in M&I
section 1.2.
Note that several of these constructions
rely on some foundations that assert the existence of points of
intersection
of circles. Thus these constructions will not be guaranteed to be
effective in a geometric structure where such points do not exist- such
as the geometry of the rational number plane.
Some comments about Constructions: It is important
to notice that constructions also require a justification
(proof) that
the construction has in fact been achieved.
In proving the constructions
we use some basic euclidean results, such as the congruence of all
corresponding
sides in two triangles is sufficient to imply the triangles are
congruent
(SSS). [Other basic Euclidean results are SAS and ASA congruence
conditions,
as well as the result that corresponding parts of congruent triangles
are
congruent (CPCTC).]
For these particular constructions to be
justified by the same arguments given by Euclid in a geometric
structure, the structure will need both an equivalence relation called
congruence for line segments, angles, triangles and propositions that
connect congruence of triangles to sufficient conditions
like SSS, SAS, and ASA.
The constructions play two
important but different roles in (euclidean) geometry:
(i) Construction allow us to "move", deconstruct and reconstruct
figures, while maintaining the magnitudes of the pieces and angles .
Thus constructions provide the tools for transformations such as
rotations and translations.
(ii) Constructions allow us to develop comparative measurements based
on a "unit" segment and the "straight" angle.
It should also be noted that the three
transformations
(translation, rotation, and reflection) commonly used in geometry are
connected
to constructions as well. For example, to translate a figure by a
vector
it would be useful to know how to construct parallelograms.
Note on midpoints: With the construction
of
midpoints in Euclidean Geometry, we can show that a Euclidean line
segment
has an infinite (not finite) number of distinct points. Furthermore, if
we think of approximating real number distance with points on a segment
after establishing a unit length, then we can construct the position of
a euclidean point as close as we want to the position where a real
number
might correspond to a point in that position.
- The construction of points that
correspond to
numbers
on a line.
First construct `P_k` where `k` is an integer using circles.
We can construct points with fractions using powers of `2` for the
denominator
by bisection.
(However, with only bisection we could not construct a point for
`1/3`
although we could get very close to that point using a binary
representation
of that common fraction.) Using midpoints of segments we can
construct points that correspond to `n/(2^k)` for any `n` and `k`.
Unfortunately real numbers like `sqrt{2}` and `pi` cannot be
expressed in this way. To obtain a correspondence of points with all
real numbers using bisection we need a geometric property that will
give a point to correspond to any convergent sequence of numbers of the
form `n/(2^k)`.
The continuity axiom for a euclidean line:
- Any non empty family
of
nested segments
will have at least one point in the intersection of the family.
This axiom allows us to make a 1 to 1 correspondence between any real
number
and a point on a euclidean line once points have been determined to
correspond
to 0 and 1.
I.e., given P0 and P1
for any
real number x where a<x<b there is a point Px
where Px is between Pa
and Pb if
and only if the point `P_{n/(2^k)}` corresponds
to the number `n/(2^k) ` for any integer `n` and natural number `k`
.
[Review the construction of a line though a given point parallel to
a given line. See Euclid
I.31.]
We can also construct Pk when k is a rational number using the theory
of similar triangles.
For example: We can bisect or trisect a line segment, giving us
the
ability to find points representing rational numbers with denominators
involving powers or 2 and 3, such as `5/6, 7/18`, etc.
The figure below gives two ways to achieve these constructions. One
can see how to generalize these to allow one to construct points to
represent
any rational number on the line so that the arithmetic of numbers is
consistent
with the arithmetic of geometry. [Adding segments and adding numbers,
etc.]
Consider M&I's constructions of the same
correspondence of
integer and rational points. These also rely on the ability to
construct
parallel lines.
Introducing Orthogonal Circles and The inverse of a
point with respect to a circle. Convexity of a geometric figure.
Tangents to circles.
In considering constructions of tangents to circles we use the
characterization
of a tangent line as making a right angle with a radius drawn at the
point
it has in common with the circle. ( Book
III
Prop.
16.) In our construction, not Euclid's (Book
III
Prop.
17), we also use the result that any angle inscribed in a
semi-circle is a right angle. ( Book
III
Prop.
31.)
Note on Three
Historical Problems of Constructions.
(1) Trisection of an angle: Since it
possible
to bisect and trisect any line segment and bisect any angle, the issue
is, is it possible to trisect any angle?
(2) Duplication of a cube: Since it is
possible
to construct a square with twice the area of a given square, the issue
is, is it possible to construct a cube with twice the volume of a given
cube?
(3) Squaring a circle: Since it is possible
to construct a square the same area as any given polygonal region, the
issue is, is it possible to construct a square with the same area as a
given circle.
Doing arithmetic
with constructions in geometry. Note
that the construction above allows one to construct a point Px' from a
point Px as long as x is not 0 so that x' x = 1.[ Use the circle of
radius
1 with center at P0 to construct the inverse point for Px.]
The relation of the
inversion
transformation with respect to a circle and orthogonal circles.
Proposition: If
C2 is orthogonal to C1 (with center O) and A is a point on
C2 then the ray OA will intersect C2 at the point A' where A and A' are
inverses with respect to the circle C1. Click
here for the proof.
We can use this proposition in the following
Constructions: 1. Construct a circle C2 through a given
point
B on a circle C1 and a point A inside the circle so that C2 is
orthogonal
to C1.
Solution: First construct the inverse A' of A with
respect
to C1 and then the tangent to C1 at B and the perpendicular bisector of
AA' will meet at the center of the desired circle.
2. Construct a circle C2 through two points A and B inside
a circle C1 so that C2 is orthogonal to C1.
Solution: This solution is demonstrated in the sketch below.