Martin Flashman's Courses - Math 371 Spring, '16
Geometry Notes
Geometric Structures for the Visual
[Work in Progress DRAFT VERSION Based on notes from 09 and 11]
The use of Java has become a browser and machine dependent issue.
In particular, the Java used in David Joyce's version of Euclid does not work uniformly in Firefox on HSU computers, but does seem to work on Chrome. Other Java works in Firefox, but not in Chrome. I will try to indicate these dependencies when possible.
Readers who might have difficulty running the Java applets are advised to use a book marklet that converts JavaSketchpad sketches on this page (or anywhere else on the internet) to work completely independently of Java.
Go to this site http://dn.kcptech.com/builds/804.12-r/cdn/bookmarklet.html to install the small tool in your web browser OR
click on the following link to "fix" the java. Convert JavaSketch
Please give feedback, whether bug reports or other, at the following email address: wsp@kcptech.com
| Week |
|
Wednesday |
|
| 1 |
|
1-20 Introduction |
1-22 Continue discussion of what
is "geometry"? Start on Euclid- Definitions, Postulates, and Prop 1. |
| 2 |
1-25 Euclid- Definitions, Postulates,
and Prop 1. cont'd |
1-27 Pythagorean plus. |
|
| 3 |
2-1 Euclid early Props/ Pythagoras/ |
2-3 Euclid early Props/ Pythagoras/ |
2-5 Equidecomposable polygons |
| 4 |
2-8 More on Details for triangulation of planar polygonal regions and adding parallelograms. |
2-10 Begin Constructions and the real number line M&I's Euclidean Geometry |
2-12 Constructions from M&I. |
| 5 |
2-15 Begin Constructions and the real number line. | 2-17 Similar Triangles.Intro to Proportions. Construction of rational numbers. Constructions and The real number line.- Continuity | 2-19
Coordinate based proofs.
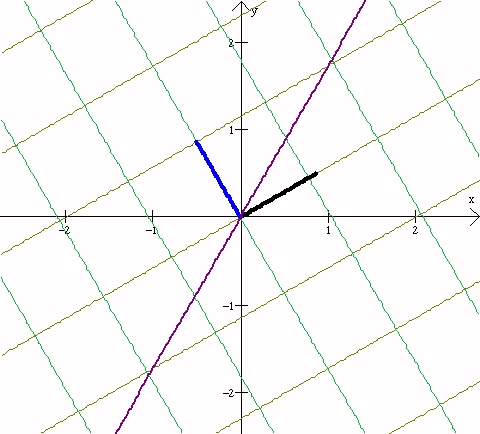
Inversion and Orthogonal Circles . Isometries:Classification of Isometries |
| 6 |
2-22 Inversion and Orthogonal Circles | 2-24 Continuity applied.. Isometries:Groups and Classification of Isometries. |
2-26 Convexity of intersections. Start Proof of classification result for plane isometries |
| 7 | 2-29 Finish Classification of Line Isometries and coordinates | 3-2 Finish
Classification
of Plane
Isometries and coordinates |
3-4 Isometries
and
symmetries Begin Affine Geometry |
| 8 | 3-7 Proportion and Similarity | 3-9 Euclidean (Eudoxus) Proportion. . |
3-11 Euclidean (Eudoxus) Proportion.and similarity, |
| 9 |
3-14 No class Spring Break! | 3-16 No class Spring Break! | 3-18 No class Spring Break! |
| 10 |
3-21 Euclidean Proportion and ratios of lengths with numbers. Central Similarity as a transformation. |
3-23 The Affine Line and
Affine
Geometry
(planar
coordinates). Affine geometry- Homogeneous coordinates for aa affine line |
3-25 The Affine Line and
Affine
Geometry
(planar
coordinates). Affine geometry- Homogeneous coordinates and Visualizing the affine plane. |
| 11 |
3-28 Watch Non-Euclidean Universe (Open Univ. Video)- Lib. |
3-30 The 7 point Geomoetry. Axioms and Stuctures |
4-1 Watch Conics (Open Univ. Video)- Lib. |
| 12 |
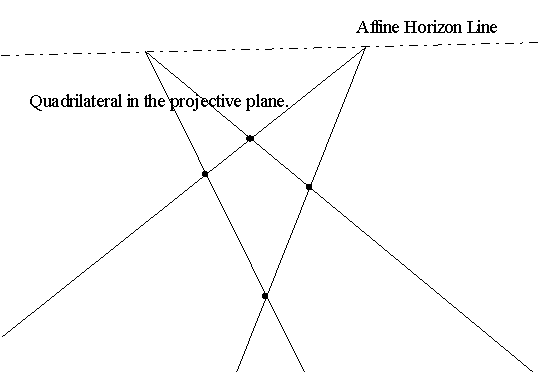
4-4 Affine geometry- Homogeneous coordinates and Visualizing the affine plane. | 4-6 More on Affine Projective Geometry - Algebra! |
4-8 Desargues!
|
| 13 |
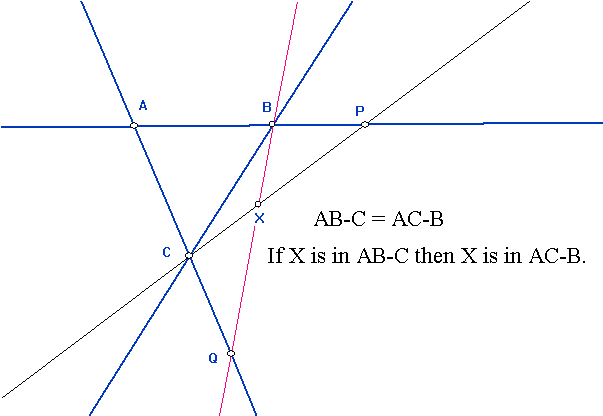
4-11 Review and start of Synthetic Projective Geometry |
4-13 More Review and start of Synthetic Projective Geometry | |
| 14 |
4-18 Proofs - planes in Projective Geometry |
4-20 A start on transformations with homogeneous coord.s. The Planar Duality Principle |
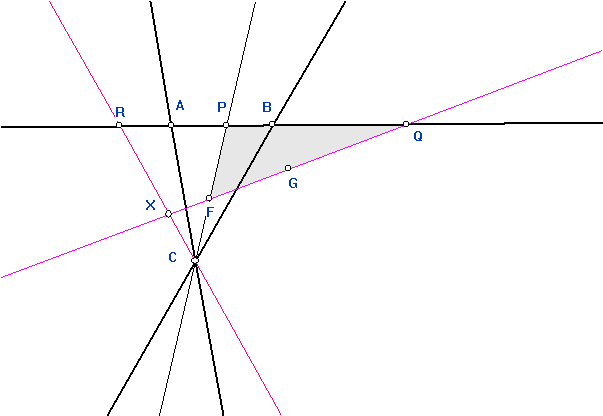
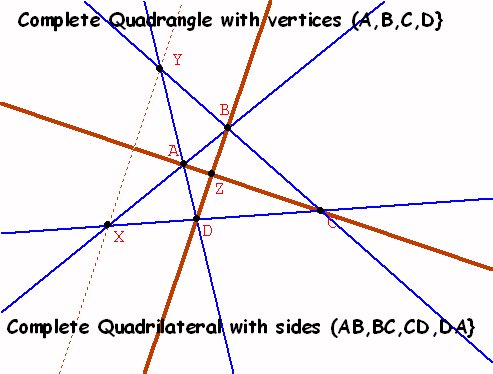
4-22 Complete quadrangles. 3 dimensions, Sections and perspectivities. |
| 15 |
4-25 Projectivities and harmonics |
4- 27 | 4-29 |
| 16 |
5-2 |
5-4 | 5-6 |
- 1-20/22 Introductory Classes Summary (+).
What are different aspects of geometry? How is the study of geometry organized? Analytic(numbers) , Synthetic(axiomatic), Transformations (functions) are three ways to organize information and the study of geometry. Also Projective and Differential geometry were mentioned as alternative focuses for studying geometry.
- The Course
Description was discussed. Still to be covered is the course project on the assignments webpage.
- Additional Relevant Notes:
- Different types of geometry:
- Euclidean: Lengths are important
- Similarity: Shape is important
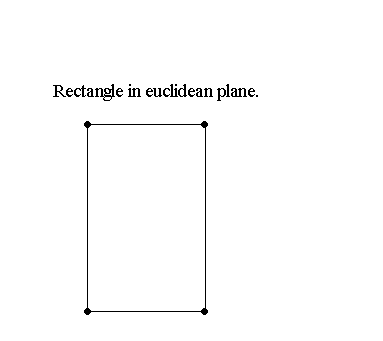
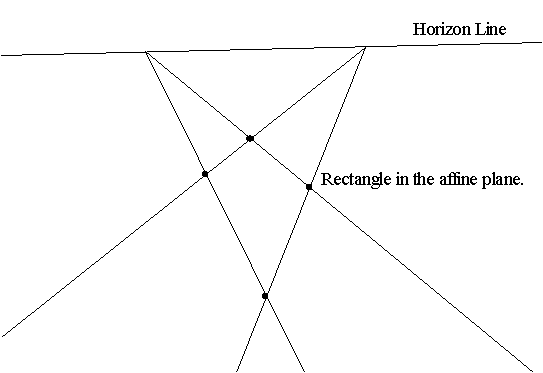
- Affine: Parallel lines are important.
- Projective: "Shadows" are important
- Differential: Curvature is important.
- Topological: General shape- especially holes and connectedness- is important.
- What is synthetic geometry? A geometry that focuses on connecting statements (theorems, constructions) to a foundation of "axioms" by using proofs.
- What is analytic geometry? A geometry that focuses on connecting statements (theorems, constructions) to a foundation of number based algebra.
- What is "structural geometry"? A geometry that focuses on connecting statements (theorems, constructions) to a foundation of structures (relations and operations) on sets by using proofs.
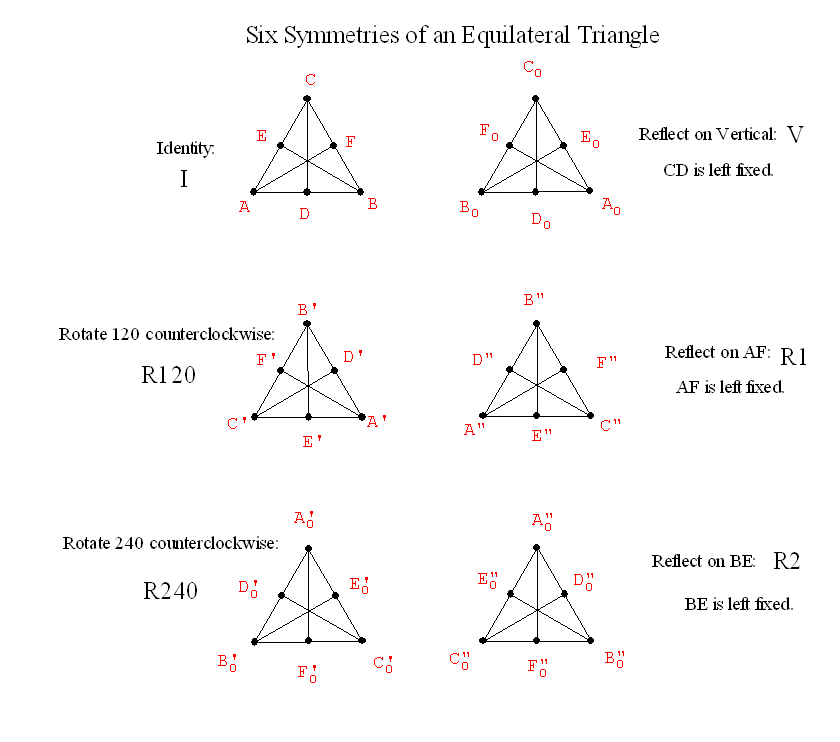
- transformations: tools that allow for changing figures:[the basis for studying different geometries in the Klein Erlangen Program. See Felix Klein - YouTube Felix Klein (25 April 1849 – 22 June 1925)
- Euclidean: translations, rotations, and reflections.
- Similarity: magnifications, dilations
- Affine: Preserve parallel lines
- Projective: "linear projections"...line preserving
- Differential: "smooth".
- Topology: continuous
- geometry as an empirical science
- geometry as a formal system of information
- geometry focused on special objects like triangles, or special qualities like convexity.
- A figure C is called convex if given any two points in the figure, A and B, the line segment AB is a subset of the figure.
- Examples. An elliptical region in the plane is convex. A lunar region in the plane is not convex. [Here is an interesting piece of geometry related to the area of lunes.]
- Geometry on the web and using GeoGebra
- Geometry has traditionally been interested in both results-
like
the
Pythagorean
Theorem- and foundations - using
axioms
to justify the result in some rigorous organization. We will be
concerned
with both results and foundations.
- We will attempt to build an understanding of both the synthetic and analytic approaches to geometry by using the tools of a structural approach.
- In the distinction between
synthetic and analytic geometry the key connecting
concept is the use of measurements.
- Initially we will try to avoid when possible the use of measurement based concepts in the structures we use .
- Consider the on-line version of Euclid's
Geometry- especially Book
1:
- The list (on-line) of initial definitions and postulates. ( We will continue a discussion of these in more detail later in the course.) The end results of Book I are The Pythagorean Theorem and its converse.
- Consider Proposition 1 and that statement appear justified by the definitions and postulates! A more detailed
discussion of this proposition is found below.
- Discuss: What would we need in geometry to make a proof of the PT based on this activity?
- What kind of structures and assumptions were
needed in the proof with the 4 triangles and squares?
Here are some considerations related to those assumptions: - What types of objects are being considered?
- points
- lines
- line segments
- angles
- triangles
- squares
- What types of relations are being considered?
- points on lines
- Lines intersecting at points
- Congruent line segments
- congruent angles
- congruent figures (triangles, squares)
- Decomposing and recomposing a figure.
- How could we justify identifying "equal" objects (congruent figures)?
- How do the objects fit together?
- How do movements effect the shapes of objects.
Consider the Pythagorean Theorem Activity Sheet.
- Back to Euclid for some further examination of the postulates:
- Looking at the definitions and postulates, a key feature of any geometric structure appears early- What defines a point and a line?
- An alternative- minimal geometry: points: A,B. lines: {A,B}. That's all!
- Postulate 1. To draw a straight line from any point to any point.
- Current view: Two distinct points determine a unique straight line.
- Issue: What
is a "straight" line?
- Alternative
geometry- spherical. Points: points on a unit sphere in coordinate
space: { (x,y,z): x2 + y2
+ z2=1}
Straight lines: Great Circles on the sphere. Determined by a plane in space through (0,0,0).
Fact: Two points on the sphere that are not antipodal- (Opposite) determine a unique straight line. [Use the plane determined by the two points and (0,0,0).] For this to make this spherical geometry satisfy Post 1- redefine what "distinct" means: If the points on the unit sphere are antipodal, then they are considered "equal" and thus not distinct.
- Postulate 2. To produce a finite straight line continuously in a straight line.
- Current view: A straight line has no "endpoints".
- Issue: What
is the nature of a straight line not being "finite"?
Alternative Geometry. Points: all numbers in an open interval {x: 0<x<1}. Straight line: The interval (0,1) and all subintervals.
A "finite" straight line: Any closed sub-interval of (0,1).
Fact: Any closed sub-interval of (0,1) is properly contained in another closed subinterval of (0,1).
Proof: Suppose 0<a,b<1. Then [a,b] is contained in the interval `[a/2, (b+1)/2]` which is contained in (0,1). - Postulate 5. That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
- Current view:
Under the given circumstances, the two straight lines are not
parallel.
Issue: How can you find the actual point where the lines meet?
Here is the most distinctive of the postulates that appear in Euclid.
The definition of parallel: Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction. - Looking at "Common Notions" we see the geometry has
language for equality and addition- a relation and an operation for the
objects.
- 2-1
- Look at how the definitions and postulates are used in Euclid:
- Consider Euclid's Proposition 1 and Proposition 2.
- These propositions demonstrate that Euclid did not treat moving a line segment as an essential property worthy of being at the foundations as an axiom. However, this is a fundamental tool for all of geometry.
- Note that in the proof of proposition 1 the point of
intersection
of circles is presumed to exist without reference to any of the
postulates.
This presumptions was left implicit for hundreds of years, but were
cleared
up in the late 19th century (see the work of David Hilbert) when
careful attention was given again to the axioms
as a whole system.
- Notes on Existence:
Existence is an often
overlooked quality in a mathematical statement:
For example it is common to state that `sqrt{2}` is an irrational number.
The proof starts by assuming `sqrt{2}` is a rational number, say `sqrt{2} = p/q` where `p` and `q` are natural numbers, so that ... `2 q^2 = p^2`. From this the usual proof of the statement deduces a contradiction. However, the statement assumes that there is a number the square of which is equal to `2`.
One can justify the existence of the square root of `2` in many ways. One way presumes that any line segment has a length measured by a real number. Then by the Pythagorean theorem, the diagonal of a unit square will have length `sqrt{2}`.
- Alternative "rational coordinate" plane geometry. [A geometry in which circles do not always intersect.] Points: ordered pairs of rational numbers.
An example of a point not in the rational coordinate plane is the point `(sqrt{2},0)`. This point can be constructed in the ordinary plane with straight edge and compass using the circle with center `(0,0)` and radius determined by the points `(0,0)` and `(1,1)`. This circle will meet the X-coordinate axis at the point `(sqrt{2},0)`
The circle with center `(0,0)` and radius `1` and the circle with center `(1,0)` and radius `1` meet in the ordinary plane at the points with coordinates `(1/2, sqrt{3}/2)` and `(1/2, -sqrt{3}/2)` . Since `sqrt{3}/2` is not a rational number, this ordered pair does not correspond to a point in the rational coordinate plane, so the two circles do not have a point of intersection in the rational coordinate plane.
- Note: Proposition 1 has a statement that was
not justified by the definitions and postulates!
- Proposition 2 demonstrates a concern of Euclid about establishing a "motion" or transformation for this geometry based on fundamental postulates.
- An example of the "web" of information formed in this
"axiomatic" synthetic geometry.
- Not just demonstrations- but the first two propositions are dedicated to constructions! A focus on existence as well as conditions that guarantee other conditions.
2-3 Some Comments on Problem Set #1:Intersections for families of convex figures:
Using the notation of M & I:
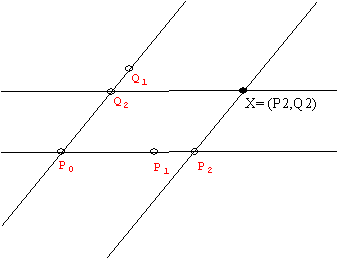
`cap \{ [P_0P_r : r>0\} = \{P_0\} ; cap \{ [P_{-1-r}P_{1+r} : r>0\} = \{P_{-1}P_1\}`
To show that `\D = `{`P` in plane where `d(P,P^*) le 1`} is convex where `P^*` is a point in the plane,
recognize that `D = cap` { half planes determined by tangent lines to the boundary of `D` that contain `P^*`}. These half planes are all convex.
- Note that M&I build an informal presentation of a
geometry structure based on using the real numbers.
- To explore some of these issues, let's looked at the Pythagorean Theorem and its proofs.
- Consider Euclid's statement and proof of Proposition 47.
- Measurement
and the Pythagorean
Theorem (PT)
Note that Euclid's treatment in its statement or its "proof"
never refers
the traditional equation, a2+b2=c2.
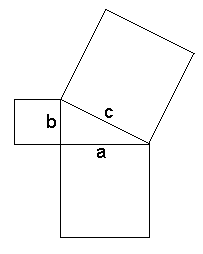
a2 + b2 = c2
-
Another
proof
using "shearing" illustrated in the GeoGebra visual proof by
choosing "Shear Pythogoras"and the Java sketch below taken from
a Geometers' Sketchpad example that can be connected to Euclid's proof.
-
Shear the squares on the legs by dragging point P, then point Q, to the line. Shearing does not affect a polygon's area.
-
Shear the square on the hypotenuse by dragging point R to fill the right angle.
-
The resulting shapes are congruent.
-
Therefore, the sum of the squares on the sides equals the square on the hypotenuse.
[Side Trip?] Moving line segments: Can we move a line segment without changing its length.
2-5
We can look further at the foundations of the proofs of the Pythagorean Theorem in two ways:
-
1. Dissections:
How
are
figures
cut and pasted together? Can be the proof be achieved using
dissections?
2. Transformations: How are figures transformed? What transformations will leave the measurements of "area", "lengths", and "angle measures" of figures invariant (unchanged)?
A look at the
possibilities of
dissections .
- Cutting and reassembling polygons. More ....
- Dissections (like Tangrams) and equidecomposable polygons.
- Use tangram pieces to make a square.
- Note that in putting the pieces together to form any other shape, the area of that shape would be the same as the area of the square unless there is some overlap of the pieces in the shape.
- Question: Is this necessary condition of equal areas sufficient to say that two polygonal regions could be decomposed (cut and pasted) into smaller regions that would be congruent?
Comment: In a sense a positive (yes) response to this question means that one could create a set of smaller shapes with which one could make either of the two regions using precisely these smaller shapes. The answer to this question is yes (in fact this is a late 19th - early 20th century result), which is the basis for the remainder of this section
[The analogous problem in three dimensional geometry: volume equality of polyhedra is a necessary but not sufficient condition for a similar result. This was the third of the famous 23 "Hilbert problems" for the 20th century. This was first demonstrated by Dehn almost as soon as the problem was announced. Dehn used another invariant of polyhedra related to the lengths of the edges and the dihedral angles between the faces of the polyhedra.[ "Ueber den Rauminhalt," Math. Annalen, 55 (1902), 465-478].
See also A New Approach to Hilbert's Third Problem - University of ...by D Benko.
First, consider some of the background results which were known to Euclid: (1) parallelograms results and (2) triangle results. The justifications for these results can be reviewed briefly.
(1) a. Parallelograms between a pair of parallel lines and on the
same
line segment are equal (in the sense of being able to decompose one to
reconstruct the other). Proposition
35.
b. Parallelograms between a pair of parallel lines and on
congruent
segments are equal (in the sense of being able to decompose one to
reconstruct
the other). Proposition
36.
(2) a. The line segment connecting the midpoints of two
sides
of a triangle is parallel to the third side and is congruent to one
half
of the third side.
[The justification of this result is left
as an exercise in traditional Euclidean Geometry.]
b. By rotating the small triangle created by connecting the midpoints
of two sides of a triangle 180 degrees about one of the midpoints, we
obtain
a parallelogram. (This shows that the triangle's area is the area
of this parallelogram which can be computed by using the length of the
base of the triangle and 1/2 of its altitude- which is the altitude of
the parallelogram.)
Compare this with Euclid
Prop. 42 and Prop. 44.
-
2-8
(ii) The triangulation of any polygonal region in the plane is a key element in a proof of the equidecomposable polygon theorem.
The proof of this proposition examines a more careful characterization of the polygonal regions being considered. The key idea of the proof goes by induction on the number n = the number vertices = the number of sides in the polygon. Proof of the triangulation proposition.
| Intersect two pairs of parallel lines, l and l' with m and m'- one
from each of the given parallelograms. Draw a diagonal HI in the
resulting
parallelogram. Cut and translate one parallelogram so that it is scissors congruent to a parallelogram HIJK within the same parallel lines l and l' with one side being the diagonal. Cut and translate the other parallelogram so that it is scissors congruent to a parallelogram HINO within the same parallel lines m and m' with one side being the diagonal and on the other side of the diagonal HI from the transformed first parallelogram. Now draw the parallel NO to the diagonal in the second transformed parallelogram HINO so that it intersects the parallels l and l' from the first parallelogram at the points P and Q. This makes one larger parallelogram JKPQ which is scissors congruent to the original two parallelograms. Compare this with Euclid Proposition 45. |
Follow this link for a proof of the equidecomposable polygon theorem. or here is a slightly different approach.
The film Equidecomposable Polygons also proves the result:
If two polygonal regions in the plane have the same area, then
there
is a decomposition of each into polygons so that these smaller polygons
can be moved individually between the two polygons by translations or
half
turns (rotations by 180 degrees).
2-10
Footnote on Equidecomposable Polygon Theorem:
The relation of being "scissors congruent" (sc) is an equivalence relation:
- A sc A
- If A sc B then B sc A.
- If A sc B and B sc C then A sc C.
General discussion of invariants:
Geometry (and Math in general) studies objects and how they are transformed.
Some features of the objects are preserved by the transformations. These features are often described as invariants of the transformation.
In studying equidecomposable polygons, the objects are polygonal regions in the plane, and the transformations are scissors congruences.
The area of the initial polygon is the same as the area of the transformed polygon, so area is an invariant of scissor congruence.
The general question: Given some objects and transformations, what are the invariants of these transformations? Is there a collection of invariants for the transformations so that if two objects have the same invariants then they are equivalent in some sense based on the transformations being studied.
The main impact of the Equidecomposable Polygon Theorem: For planar polygons and scissors congruence, the area of the polygon is an invariant that is sufficient to determine when two polygons are or are not scissors congruent
.
Another geometric relation connected to transformations is congruence for triangles.
We will study further the transformations that are key to the congruence relation: translation. rotation, and reflection.
There are many invariants for these transformation: they include the length of segments and the measurement of angles as well as area of the triangles.
It should be clear that the area of two triangles is not enough to determine whether they are congruent.
There are some key invariants of a triangle which can determine congruence:
- The three corresponding sides of two triangles are congruent: SSS
- Two sides and the included angle of two triangles are congruent: SAS
- Two angles and the included side of two triangles are congruent: ASA.
Read the definitions in M&I section 1.1
REVIEW of basic plane geometry concepts and definitions based on M&I.
M&I build their foundations for Euclidean geometry on a one to one correspondence between points on a line and real numbers and the ability to match angles with numbers between 0 and 180.
Review materials defining rays, segments, angles, triangles, and planes in M&I.
These definitions present a model for geometry based on the real numbers. Points, rays, line segments, etc., are identified with real numbers and intervals of real numbers. Notice that angles in the plane are not oriented and are always considered to have a measure between 0 and 180.
-
2-12
Review eight of the basic Euclidean constructions described in M&I section 1.2. Note that several of these constructions rely on some foundations that assert the existence of points of intersection of circles. Thus these constructions will not be guaranteed to be effective in a geometric structure where such points do not exist- such as the geometry of the rational number plane.
| Angle Bisection | Euclid Prop 9 |
Line Segment Bisection |
Euclid Prop 10 |
Construct Perpendicular to line at point on the line |
Euclid Prop 11 |
| Construct Perpendicular to line at point not on the line | Euclid Prop 12 |
| Move an angle | Euclid Prop 23 |
| Construct Parallel to given line
through a point |
Euclid
Prop
31 |
Some comments about Constructions: It is important
to notice that constructions also require a justification
(proof) that
the construction has in fact been achieved.
In proving the constructions
we use some basic euclidean results, such as the congruence of all
corresponding
sides in two triangles is sufficient to imply the triangles are
congruent
(SSS). [Other basic Euclidean results are SAS and ASA congruence
conditions,
as well as the result that corresponding parts of congruent triangles
are
congruent (CPCTC).]
For these particular constructions to be
justified by the same arguments given by Euclid in a geometric
structure, the structure will need both an equivalence relation called
congruence for line segments, angles, triangles and propositions that
connect congruence of triangles to sufficient conditions
like SSS, SAS, and ASA.
The constructions play two
important but different roles in (euclidean) geometry:
(i) Construction allow us to "move", deconstruct and reconstruct
figures, while maintaining the magnitudes of the pieces and angles .
Thus constructions provide the tools for transformations such as
rotations and translations.
(ii) Constructions allow us to develop comparative measurements based
on a "unit" segment and the "straight" angle.
It should also be noted that the three
transformations
(translation, rotation, and reflection) commonly used in geometry are
connected
to constructions as well. For example, to translate a figure by a
vector
it would be useful to know how to construct parallelograms.
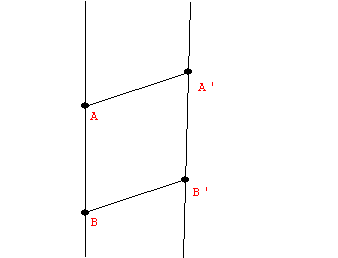
We reviewed the connection between the Euclidean constructions and the three transformations (translation,
rotation, and reflection) and the fact that if T is either a
translation, determined by a vector ( an oriented line segment), a
rotation determined by a center and an oriented angle, of a reflection,
determined by a line, the image if a triangle `T( Delta ABC) = Delta
A'B'C'` is a triangle that is congruent to `Delta ABC`.
Other properties of these transformations, that preserve measure of line
segments and congruence of angles, as well as similarities will be
discussed further.
Note on midpoints: With the construction of midpoints in Euclidean Geometry, we can show that a Euclidean line segment has an infinite (not finite) number of distinct points. Furthermore, if we think of approximating real number distance with points on a segment after establishing a unit length, then we can construct the position of a euclidean point as close as we want to the position where a real number might correspond to a point in that position.
- The construction of points that correspond to numbers on a line.
- Any non empty family of nested segments will have at least one point in the intersection of the family.
First construct `P_k` where `k` is an integer using circles.
We can construct points with fractions using powers of `2` for the denominator by bisection.
(However, with only bisection we could not construct a point for `1/3` although we could get very close to that point using a binary representation of that common fraction.) Using midpoints of segments we can construct points that correspond to `n/(2^k)` for any `n` and `k`. Unfortunately real numbers like `sqrt{2}` and `pi` cannot be expressed in this way. To obtain a correspondence of points with all real numbers using bisection we need a geometric property that will give a point to correspond to any convergent sequence of numbers of the form `n/(2^k)`.
The continuity axiom for a euclidean line:[Cantor's Axiom]
I.e., given P0 and P1 for any real number x where a<x<b there is a point Px where Px is between Pa and Pb if and only if the point `P_{n/(2^k)}` corresponds to the number `n/(2^k) ` for any integer `n` and natural number `k` .