|
|
Wednesday |
|
|
|
1/22 Introduction |
Start on The Pythagorean Theorem |
|
|
1/29 Dissections |
Begin M&I's Euclidean Geometry |
|
|
2/5 More on Constructions and the real number line. |
|
|
|
2/12 Classification of Isometries & More :) | 2/14 More on Isometries. |
|
|
2/19 Similarity and proportion |
|
|
|
2/26 Inversion and Beginning to See The Infinite. | 2/28 More on seeing the infinite. |
|
|
3/5 More on The Affine Line and Homogeneous Coordinates and the Affine Plane |
|
|
|
3/12 Connecting Axioms to Models. Introduction to projective geometry with homogeous coordinates. |
Video Orthogonal Projection. |
|
|
3/19 No class Spring Break! |
|
|
Introduction to Desargues' Theorem- a result of projective geometry. |
3/26 More on Visual and algebraic models for plane geometry. More axioms for synthetic projective plane geometry. |
|
|
|
4/2 More examples of proofs in synthetic projective geometry. Proof of Desargues' Theorem in the Plane. |
|
|
|
4/9 Sections and Perspectively related Figures |
|
|
|
4/16 Projective Line transformations: Synthetic Projectivities; Matrices |
|
|
|
|
|
|
|
4/30 |
|
|
|
5/7 |
|
Note that Euclid's treatment in its statement or its "proof" never refers the traditional equation, a2+b2=c2.
Notes on Existence: Existence is an often
overlooked quality in a mathematical statement:
For example it is common to state that sqrt(2)
is an irrational number.
The proof starts by assuming sqrt(2) is a rational
number, say sqrt(2) = p/q where p and q are natural numbers, so that
... 2 q2 = p2. From this the usual proof of
the statement deduces a contradiction. However, the statement assumes
that there is a number the square of which is equal to 2.
One can justify the existence of the square root
of 2 in many ways. One way presumes that any line segment has a length
measured by a real number. Then by the pythagorean theorem, the diagonal
of a unit square will have length sqrt(2).
An example of a geometry where circles do not
intersect is given by using the rational coordinate plane.
Points correspond to ordered pairs of rational numbers.
The circle with center (0,0) and radius 2 and
the circle with center (2,0) and radius 2 meet in the ordinary plane at
the points with coordinates (1, sqrt(3)) and (1, -sqrt(3)) . Since sqrt(3)
is not a rational number, this ordered pair does not correspond to a point
in the rational coordinate plane, so the two circles do not have a point
of intersection in the rational coordinate plane.
Another example of a point not in the rational coordinate plane is the point (sqrt(2),0). This point can be constructed in the ordinary plane with straight edge and compass using the circle with center (0,0) and radius determined by the points (0,0) and (1,1). This circle will meet the X-coordinate axis at the point (sqrt(2),0)
A look at the possibilities of dissections .
First, consider some of the background results which were known to Euclid: (1) parallelograms results and (2) triangle results. The justifications for these results can be reviewed briefly.
(1) a. Parallelograms between a pair of parallel lines and on the same
line segment are equal (in the sense of being able to decompose one to
reconstruct the other). Proposition
35.
b. Parallelograms between a pair of parallel lines and on congruent
segments are equal (in the sense of being able to decompose one to reconstruct
the other). Proposition
36.
(2) a. The line segment connecting the midpoints of two sides
of a triangle is parallel to the third side and is congruent to one half
of the third side.
[The justification of this result is left
as an exercise in traditional Euclidean Geometry.]
b. By rotating the small triangle created by connecting the midpoints
of two sides of a triangle 180 degrees about one of the midpoints, we obtain
a parallelogram. (This shows that the triangle's area is the area
of this parallelogram which can be computed by using the length of the
base of the triangle and 1/2 of its altitude- which is the altitude of
the parallelogram.)

For more discussion of proofs of this proposition see Triangulations and arrangements, Two lectures by Godfried Toussaint, transcribed by Laura Anderson and Peter Yamamoto.
How to "add two parallelograms to form a single parallelogram which
is scissors congruent to the two separate parallelograms":
Intersect two pairs of parallel lines, l and l' with m and m'- one
from each of the given parallelograms. Draw a diagonal HI in the resulting
parallelogram.
Cut and translate one parallelogram so that it is scissors congruent
to a parallelogram HIJK within the same parallel lines l and l' with one
side being the diagonal.
Cut and translate the other parallelogram so that it is scissors congruent
to a parallelogram HINO within the same parallel linesm and m' with one
side being the diagonal and on the other side of the diagonal HI from the
transformed first parralleogram. Now draw the parallel NO to the diagonal
in the second transformed parallelogram HINO so that it intersects the
parallels l and l' from the first parrallelogram at the points Pand
Q. This makes one larger parallelogram JKPQ which is scissors congruent
to the original two parallelograms.
Follow this link for the proof of the equidecomposable polygon theorem.
The film Equidecomposable Polygons also proves the result:
If two polygonal regions in the plane have the same area, then there
is a decomposition of each into polygons so that these smaller polygons
can be moved individually between the two polygons by translations or half
turns (rotations by 180 degrees).
Some comments about Constructions: It is important to notice that constructions also require a justification (proof) that the construction has in fact been achieved. In proving the constructions we use some basic euclidean results, such as the congruence of all corresponding sides in two triangles is sufficient to imply the triangles are congruent (SSS). [Other basic Euclidean results are SAS and ASA congruence conditions, as well as the result that corresponding parts of congruent triangles are congruent (CPCTC).]
It should also be noted that the three transformations
(translation, rotation, and reflection) commonly used in geometry are commected
to constructions as well. For example, to translate a figure by a vector
it would be useful to know how to construct parrallelograms.
Note on midpoints: With the construction of midpoints in Euclidean Geometry, we can show that a Euclidean line segment has an infinite (not finite) number of distinct points. Furthermore, if we think of approximating real number distance with points on a segment after establishing a unit length, then we can construct the position of a euclidean point as close as we want to the position where a real number might correspond to a point in that position.
Tangents to circles.
In considering constructions of tangents to circles we use the characterization
of a tangent line as making a right angle with a radius drawn at the point
it has in common with the circle. ( Book
III Prop. 16.) In our construction, not Euclid's (Book
III Prop. 17), we also use the result that any angle inscribed in a
semi-circle is a right angle. ( Book
III Prop. 31.)
For example: We can bisect or trisect a line segment, giving us the
ability to find points representing rational numbers with denominators
involvingpowers or 2 and 3, such as 5/6, 7/18, etc.
The figure below gives two ways to achieve these constructions. One
can see how to generalize these to allow one to construct points to represent
any rational number on the line so that the arithmetic of numbers is consistent
with the arithmetic of geometry. [Adding segments and adding numbers, etc.]
Consider M&I's constructions of the same correspondence of
integer and rational points. These also rely on the ability to construct
parallel lines.
The continuity axiom for a euclidean line:
I.e., given P0 and P1 for any real number x there is a point Px where a<x<b if and only if Px is between Pa and Pb and the point Pk . corresponds to the number k for any rational number k.
The continuity axiom can also be used to prove: If a line, l, (or circle, O'A') has at least one point inside a given circle OA and one point outside the same given circle then there is of a point on the line (circle) that is also on the given circle.
Proof outline for the line-circle:Use bisection between the points on the line l outside and inside the circle OA to determine a sequence on nested segments with decreasing length approaching 0. The point common to all these segments can be shown to lie on the circle OA.
Proof outline for the circle-circle: Draw the chord between the inside and outside points on the circle O'A'. Use bisection on this chord to determine rays that by the previous result will meet the circle O'A'. The bisections can continue to determine a sequence of nested segments with decreasing length approaching 0 and with endpoints determining one outside point and one inside on O'A' . The point common to all the endpoints on the chord will determine a point on O'A' that can be shown to also lie on OA.
Note: The circle-circle result fills in a hole
in the proof of Proposition 1 in Book I of Euclid.
The half plane example:Consider the half plane determined by a line l and a point P not on the line. This can be defined as the set of points Q in the plane where the line segment PQ does not meet the line l. Discuss informally why the half plane is convex.
Review the problems on convex figures in Problem Set 1.
Other convex examples: Apply the intersection property [The intersection
of convex sets is convex.] to show that the interior of a triangle is convex.
Show that the region in the plane where (x,y) has y>x2
is convex using the tangent lines to the parabola y=x2 and the
focus of the parabola to determine a family of half planes whose intersection
would be the described region.
Line Isometries: Consider briefly isometries of a
line.
1) translations and 2) reflections.
How can we visualize them?
Transformations figures (before and after lines) T: P -> P'; Correspondence
figures on a single line; Graph of transformation;
Coordinate function. x -> x' = f (x)
We looked at examples: P x -> Px+5 a translation;
P x -> P-x a reflection. We showed that these
were isometries of the line.
Can we classify them? Is every line isometry either a translation or
a reflection?
Plane Isometries: Consider isometries of a plane.
1) translations 2) rotations and 3) reflections.
How can we visualize them?
Transformations figures (before and after planes); Correspondence figures
on a single plane;
Coordinate function? Still to be considered....
Remark: An isometry of the plane is completely determined by
the correspondence of three non-colinear points.
We will verify more carefully in later work.
Fact: If T and S are isometries then ST is also an isometry
where ST(P) = S(T(P))= S(P') [T(P)=P'].
Proof : Consider d(ST(P),ST(Q)) = d( S(T(P)),S(T(Q)) ) = d(S(P'),S(Q'))
= d(P',Q') = d(P,Q) .
Can we classify the isometries? Is every line isometry either a translation
or a reflection?
There are at least four types of isometries of the plane: translation,
rotation, reflection and glide reflection.
2/12 The classification
of isometries.
Recall the informal definition of an isometry: A transformation (function)
that preserves "distance."
Translation: T: P (x,y) -> P(x+5, y+2)
is a translation of the plane by the vector <5,2>. If we use the coordinates
for the point and T(x,y) = (x',y') then x' = x+5 and y' = y+2. We
can express this with vectors <x',y'> = <x,y> + <5,2>. So translation
corresponds algebraically to the addition of a constant vector.
Reflections: Across X-axis RX(x,y) = (x,-y); Across Y axis RY(x,y)
= (-x,y); Across Y=X , R(x,y)=(y,x). Notice that these can be accomplished
using a matrix operation. Writing the vectors as column vectors
|
|
|
Notice that if T is an isometry, then T
is 1:1 and onto as a function.
Proof: 1:1. Suppose that T(P)=T(Q). Then d( T(P),T(Q))=0=d(P,Q)
so P=Q.
onto. Suppose R is in the plane. Consider A,B, and C in the
plane where C is not on the line AB. Then the points T(A),T(B), and T(C)
form a triangle and using the distances d(T(A),R), d(T(B),R), and d(T(C),R),
we can determine a unique point X in the plane where d(A,X)=d(T(A),R),
d(B,X) = d(T(B),R), and d(C,X)=d(T(C),R), so T(X) = R.
Proposition: Any plane
isometry is either a reflection or the product of two or three
reflections.
Proof:
Click here!
Proposition: (i) The product of two
reflections that have the lines of reflection intersect at a point O is
a rotation with center O through an angle twice the size of the angle between
the two lines of reflection.
(ii) The product of two reflections that have parallel lines of
reflection is a translation in the direction perpendicular to the two lines
and by a length twice the distance between the two lines of reflection.
(iii)The product of three reflections is either a reflection or
a glide reflection.
Proof: To be supplied here.
Watch the video Isometries (Video
# 2576 in Library) .
More on plane isometries and coordinates:
Rotations:
If R90 is rotation about (0,0) by 90 degrees, then R90(x,y) = (-y,x).
Question: What is rotation about (0,0) by t degrees?
Hint: What does the rotation do to the points (1,0) and (0,1)? Is this
rotation a "linear transformation?"
More general Question: What about reflection RAB about the line AX+BY
= 0?
|
|
|
Consider that P(1,0) will be transformed to P'(cos(t), sin(t))= (a,c) and Q(0,1) will be transformed to Q'(-sin(t), cos(t))=(b,d) |
|
|
| Orientation
Preserving |
Orientation
Reversing |
|
| Fixed points | Rotations | Reflections |
| No Fixed points | Translations | Glide reflections |
An Applications of Reflection:
(i) Here is a problem encountered frequently in
first semester of a calculus course.
The
Carom Problem Can you see how the solution is related to a "carom"
(angle of incidence=angle of reflection)?
(ii) Here is a similar problem about triangles
that is also related to reflections.
Fano's
Problem Can you find the relationship?
Symmetry of a figure: S is a symmetry
of a plane figure F if
S is an isometry with S(F)=F.
Given
a figure F, the symmetries of F
form a subgroup of all the plane isometries, denoted Sym(F).
Example: Consider the figure F=
an given equilateral triangle. We looked at the six symmetries of this
figure and the table indicating the multiplication for these six isometries.
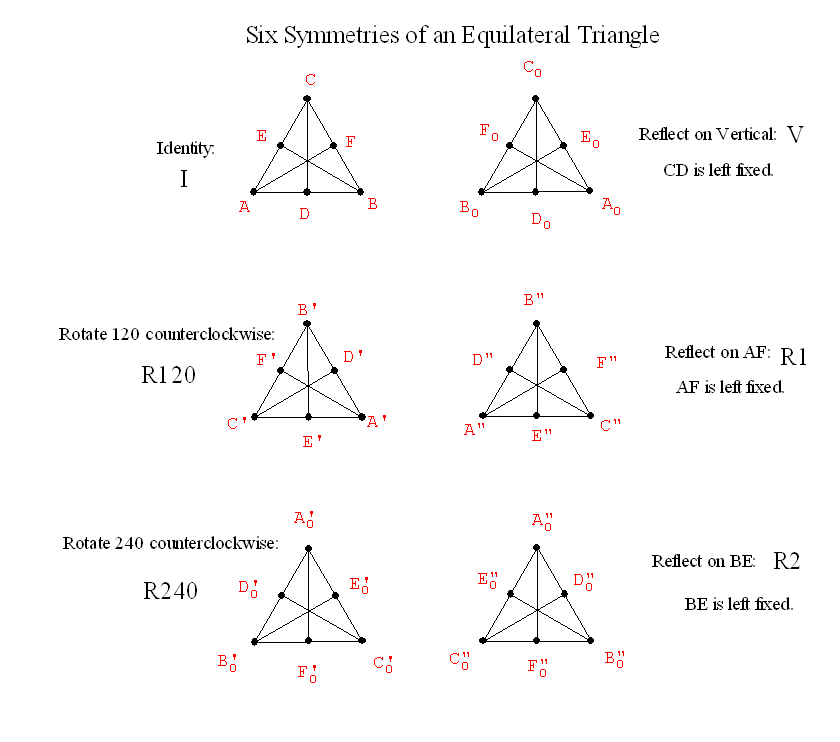
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R120 |
|
|
|
|
|
|
|
|
Repeated use of this algorithm suggests the
Euclidean algorithm for finding a common unit to measure both n and d,
or ON and OD.
If r1=0 or R1N is a point, then OD will be a common unit. If not apply
the division algorithm to d or OD and r1 or R1N. If this works to give
r2= 0 or R2N is a point, then R1N will be the common unit. If not
apply the division algorithm to r1 or R1N and r2 or R2N. If this works
to give r3= 0 or R3N is a point, then R2N will be the common unit. If not
continue. In common arithmetic since each remainder that is not zero is
smaller than the previous remainder, eventually the remainder must be 0
and the process will end- finding a common divisor of the original d and
n.
* It is Archimedes axiom that stays that any two segments either one can be used to measure the other. [There are no infinitesimals for an Archimedean geometry.]
Example: Euclid uses the theory of proportion in Book VI, Proposition 1 and Proposition 2.
We can also observe that if we let S(Px)=P(x-3) and S-1(Px)=P(x+3) then
Central similarities in the plane:
In the plane, a similarity Tm with factor m and
center
at (0,0) will transform (x,y) to (mx,my). Thus x' = mx,
and y' = my are the equations for this transformation. This transformation
can be represented using a matrix as follows:
|
Proposition: If l is a line in the plane with equation
AX+BY=C with A and B not both 0, then the set l' = {(x',y'):
Tm(x,y)=(x',y') for some (x,y) on l} is a line in the plane that
is parallel to l (unless l = l' ).
Proof (outline): Show that the equation of l' is
AX+BY = mC.
Solution: First construct the inverse A' of A with respect to C1 and then the tangent to C1 at B and the perpendicular bisector of AA' will meet at the center of the desired circle.
2. Construct a circle C2 through two points A and B inside
a circle C1 so that C2 is orthogonal to C1.
Solution: This solution is demonstrated in the sketch below.
A (set theoretic) interpretation for a geometry structure is a set in which the words of the geometry stucture's language are identified with set elements and sets and relations and operations on sets. If any true statement (theorem) about the mathematical structure is also true of the corresponding statement about the interpretation, then the interpretation is called a model for the geometric structure.
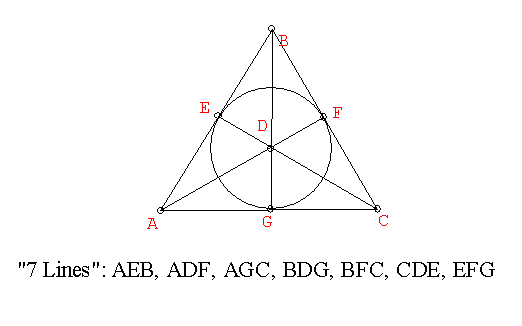
Thus we can say that an interpretation for the geometric structure described previously with point and lines is given by a set of objects labelled A,B,C,D,E,F, and G. Points correspond to the objects. Lines correspond to sets of three objects from one of the seven previously described sets: {A,E,B}, {A,D,F}... {E,F,G} . A point is on a line if the object is an element of the line set. This interpretation is a model and it is visualized by the previous "7 line" triangular figure.
Another interpretation for a geometric structure might
involve just 3 objects, A,B and C, for points and three lines {A,B}, {A,C},
and {B,C}. Although this geometry is does not satisfy the first axiom for
the previously described geometric structure, because a line does not have
three distinct points, it does satisfy the other three axioms. So
this interpretation is not a model for that structure!
However, there is something to be learned about that
structure from the two interpretations we have discussed. [To be included
here will be a discussion of how these interpretations show that it is
impossible to prove the first axiom from the other three axioms of this
structure.]
A projective plane is the geometric object made up of the collection of P-points and P-lines.
We'll call [A,B,C] homogeneous coordinates of the P-line.
For example, [1,0,1] are homogeneous coordinates
for the P-line determined by the plane with equation X + Z = 0.
[3,0,3] are homogeneous coordinates for the same P-line.
For example, <1,0,-1> are homogeneous coordinates
for the P-point determined by the line with equation (X,Y,Z) = (1,0,-1)
t. <3,0,-3> are homogeneous coordinates for the same P-point.
3/14
| + | 0 | 1 | * | 0 | 1 | ||
| 0 | 0 | 1 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | 0 | 1 |
A projective plane using F2 has exactly 7 lines:
This projective plane satisfies the geometric structure
properties described previously in the "7 point geometry".
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
Lab Exercise: Due 3/28.
| Euclidean Line: P0 and P1
Euclidean Plane: P(0,0), P(1,0), and P(0,1). Axes at right angles. Parallel lines have no point in common. |
Affine Line: P0, P1, and Pinf.
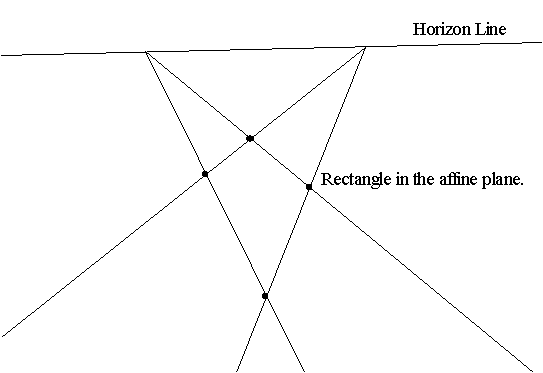
Affine Plane: P(0,0)=<0,0,1>, P(1,1)=<1,1,1>,P(inf,0)=<1,0,0>, P(0,inf)=<0,1,0> The Horizon or Ideal line. Parallel lines meet at an infinite point on the horizon. |
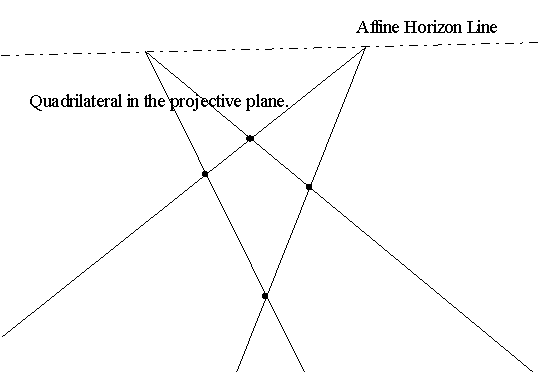
Projective Line: Pinf is treated as an ordinary point. A circle.
Projective plane: All points in the affine plane are treated as ordinary points. Homogenous coordinates determine all points and lines. There are no parallel lines. All lines meet. |
The structure established so far for the affine and projective planes.
In an affine plane there is a special line, the horizon or ideal,
line containing all the ideal infinite points for lines in the ordinary
euclidean plane. Any ordinary line has exactly one ideal infinite point
on it. Two lines in the ordinary plane are parallel if they do not meet.
Two lines in the affine plane are parallel if they meet at the same ideal
infinite point on the ideal line. In the projective plane there are no
parallel lines! We consider these statements in algebraic models for these
planes.
|
|
|
|
|
|
 |
Points:Ordinary coordinates(x,y)
Lines: Ax+By+C=0 |
|
|
 |
Points: Ordinary (x,y) or generally homogeneous <x,y,z> x,y,z not
all 0.
Lines: Ax+By+C=0 or Ax+By+Cz = 0 or [A,B,C] |
|
|
 |
Points: <x,y,z> x,y,z not all 0.
Lines: Ax+By+Cz = 0 or [A,B,C] A,B,C not all 0. |
| Where we're going in the next few weeks. We
will be discussing the following topics: the definition of the algebraic
model for the affine and projective plane and spaces, the connection of
these geometries to visualizations, and the construction of points with
corresponding coordinates in the affine line and plane using P0, P1 and
Pinfinity.
The text materials in Meserve and Izzo provides some support for these issues and should provide some support for these topics. The relevant sections are listed in the course reading assignments. |

The axioms for projective geometry in a plane uses two basic objects: points and lines, and a relation between those: a point is on a line, or a line passes through a point. The technical term for this relation is "incident", so we say a point is incident to a line and a line is incident to a point.
The dual of a statement or description in the context of a projective
plane replaces the word "point" with the the word "line" and the
word "line" with the word "point".
Here are some examples of statements and the corresponding dual statement:
| Two distinct points A and B are (incident) on a unique lineAB. | Two distinct lines a and b are (incident) on a unique point a#b. |
| If the point C is not (incident to) on the line AB then there are three lines AB, AC, and BC. | If the line c is not (incident to) on the point a#b then there are three points a#b, a#c, and b#c. |
| The lines AA', BB' and CC' are incident to the point O. | The points a#a', b#b', and c#c' are incident to the line o. |
As a consequence of this feature, plane projective has a special result which is about the theorems of geometry and their dual statments.
The Principle of Plane Projective Duality: Suppose S is a statement of plane projective geometry and S' is the planar dual statement for S. If S is a theorem of projective geometry, then S' is also a theorem of plane projective geometry.
The proof of this principle is a proof about proofs.
The idea is that a proof consists of a list of statements about lines
and points. each statement in a proof is either one of the postulates,
a previously proven theorem, or a logical consequence of previous statements.
So if we have a proof of a statement S, we have a sequences of statements
A1,A2,...,AN=S.Each of these statements is either one of the postulates,
a previously proven theorem, or a logical consequence of proevious statements.
Now one can construct the sequence of dual statements A1', A2', ...,
AN' = S'. With a little argument it can be seen that each of these dual
statements is also either a postulate, a theorem,or a logical consequence
of previous statements.
Here is an application of the principle of duality to Desargues' Theorem.
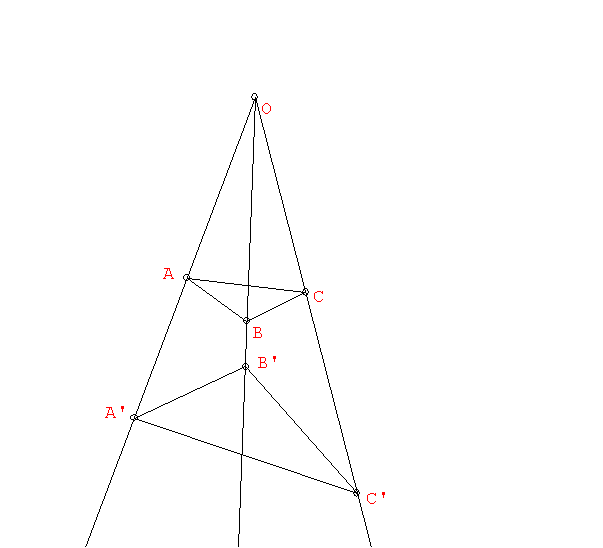
Note on Duality and the concept of perspective: We called two
point triangles ABC and A'B'C' perspectively related
with respect to a point O, if O is
on the lines AA', BB' and CC'.
We define the dual concept by saying that two line triangles
abc and a'b'c' are perspectively related with
respect to a line o, if o passes through
the points a#a', b#b' and c#c'.
Notice that the Dual of Desargues' Theorem is also the logical converse
of Desargues' Theorem. Thus we can say, "The
converse of Desargues' theorem is true by the duality principle."


|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
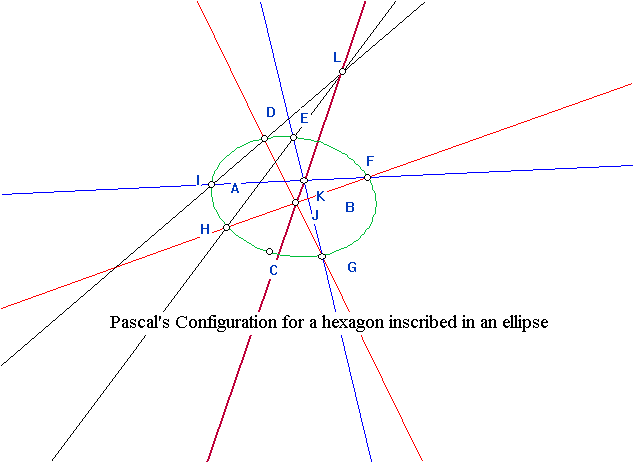
The dual concept for section: A section of a planar figure, F, by
a point L, where L is not in the figure F, is a new figure
consisting of the lines p where p = L*M for any M,
a point in the figure F.
Examples: The section of the triangle ABC by the point L, is
the set of three lines on L , {A*L,B*L, C*Ll}.
The section by a point L (not lying on a line o) of a
pencil of points on the line o is the set of lines through L with
one line for each point in the pencil.
Line Perspective in the Plane: Figure F is perspectively related
to Figure F' by the line o if there is a correspondence of the line
of F with those of F' so that for any corresponding lines, m in
F and m' in F', the line o passes through the point m#m'
.
Notes:1. If the corresponding lines in two figures F and F' are
parallel, then in the affine plane, these corresponding lines will meet
on the horizon line. Thus these figures are perpectively related in the
projective plane.
2. If the figure F and the figure F' are congruent because of a
reflection, then F and F' are prespectively related by the line of reflection.
A look at perspective of planar figures with respect to a center O and
its dual: perspective of planar figures with respect to an axis o.
A planar graph consists of a finite set of points called vertices, line (straight or curved) segments with these vertices as endpoints called edges, enclosing planar sets called regions. We can think of these regions as geographic states, the edges as boundaries between land sections, and the vertices and places where these boundaries meet.
So a planar graph G is a set of vertices, edges, and resulting regions in the plane.The dual graph of G is another graph, which for now we'll denote D(G). D(G) consists of a vertex for each region in G, a region for each vertex in G, and an edge for each edge. If R is a region in G, we choose a point in R, call it r, as a vertex of D(G). For each edge, E, of G, with regions R1 and R1 bordering on E, choose an edge, e, between r1 and r2 that crosses E. Finally, suppose V is a vertex of G. consider the edges that end at V and the regions that border these edges. Then these regions and edges correspond to vertices and edges of D(G) that surround a region which we'll denote v.
The graph D(G) consists of the vertices, r, edges, e, and regions v
just described.
One aspect of the dual graph is that information about it is revealed
by knowing information about the graph G. For example, if G has 5
regions, the D(G) has 5 vertices.
If G has 7 edges then D(G) also has 7 edges, and if G has 4 vertices,
then D(G) has 4 regions.
Take a look a this web site on Duality and Polyhedra
Here is a table showing the five platonic solids and the
duality relation of Vertices, Edges (lines), and Faces (Planes):
|
|
V |
|
|
|
|
8 |
|
|
|
|
6 |
|
|
|
|
12 |
|
|
|
|
20 |
|
|
|
|
|
|
|
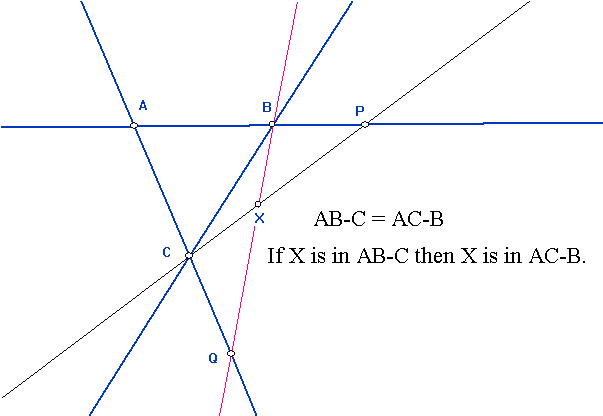
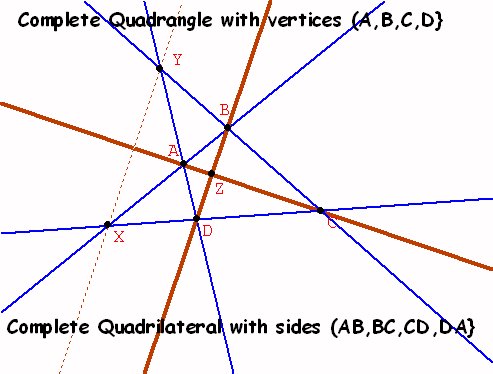 4 points {A,B,C,D} determine 6 lines {AB,AC,AD, BC, BD, CD} and three additional points {X,Y,Z}. |

The Complete Quadilateral: 4 lines {AB, BC, CD,AD}determine 6 points {A,B, C, D, X,Y} with three additional lines{AC, BD, XY} . |
Definition: The product (composition) of two
or more perpectivities is a called a projectivity.
Is we compose two perspectivities we can transform points on a line
to a second line and then back to the original line.
Thus the map from a euclidean, affine, or projective line to itself
can be a projective transformation.
Examples: Translation of a euclidean coordinate line by adding
1 unit.
T(Px) = Px+1 can be realized as a product of
perspectivities in the affine plane.
First use the perspectivity that transforms the point Px
on the X axis to the point P' = Qx+1 on the Y axis.
Then use the perpectivity that transforms the point Qx+1
on the Y axis back to Px+1 on the X axis.
Then if T represent this product of these two perspectivities, T(Px)
= Px+1.
Other examples of projective line transformations include central reflection and central similarities.
But what is the algebra for this isometry when using arbitrary homogeneous coordinates for an ordinary point?
In summary, T ( <a,b>) = <a+3b,b>.
Notice this formula works as well for the ideal point on the affine
line.
This work can be done using some ideas from linear algebra. Recall
that in matrix multiplication:
| [ | 1 | 3 | ] | [ | x | ] | = | [ | x+3 | ] |
| 0 | 1 | 1 | 1 |
| [ | 1 | 3 | ] | [ | a | ] | = | [ | a+3b | ] |
| 0 | 1 | b |
|
| [ | 1 | 3 | ] | [ | a | ] | = | [ | a+3b | ] |
| 0 | 1 | b |
|
| [ | -1 | 0 | ] |
| 0 | 1 |
| [ | -1 | 0 | ] | [ | x | ] | = | [ | -x | ] |
| 0 | 1 | 1 | 1 |
| [ | -1 | 0 | ] | [ | a | ] | = | [ | -a | ] |
| 0 | 1 | b |
|
| [ | 5 | 0 | ] |
| 0 | 1 |
| [ | 5 | 0 | ] | [ | x | ] | = | [ | 5x | ] |
| 0 | 1 | 1 | 1 |
| [ | 5 | 0 | ] | [ | a | ] | = | [ | 5a | ] |
| 0 | 1 | b |
|
| [ | 0 | 1 | ] |
| 1 | 0 |
| [ | 0 | 1 | ] | [ | x | ] | = | [ | 1 | ] |
| 1 | 0 | 1 | x |
| [ | 0 | 1 | ] | [ | a | ] | = | [ | b | ] |
| 1 | 0 | b |
|
If we let the matrix of these transformation be denoted by
| T= [ | a | b | ] |
| c | d |
| [ | a | b | ] | [ | x | ] | = | [ | ax+b | ] |
| c | d | 1 | cx+d |
| [ | a | b | ] | [ | x | ] | = | [ | ax+by | ] |
| c | d | y |
|
| [ | a | b | ] | [ | ax | ] | = | a[ | ax+by | ]. |
| c | d | ay |
|
| a[ | a | b | ] | [ | x | ] | = | a[ | ax+by | ]. |
| c | d | y |
|
| T= [ | 1 | b | ]. |
| c | d |
| [ | 1 | b | ] | [ | 1 | ] | = | [ | x | ] |
| c | d | 0 | 0 |
| T= [ | 1 | b | ]. |
| 0 | d |
| [ | 1 | b | ] | [ | x | ] | = | [ | x/d+b/d | ] |
| 0 | d | 1 |
|
| [ | 1 | b | ] | [ | x | ] | = | [ | x+by | ] |
| 0 | d | y |
|
|
lines/planes |
lines/planes |
lines[/Planes?] |
lines/planes |
| Axioms
Euclid Hilbert |
No Axioms Yet
A figure indicating an ideal point or line |
Axioms
7 points/7lines A figure. |
M & I Axioms
A figure indicating all points and lines |
| Parallel lines don't meet | Parallel lines meet
at an ideal point. |
All pairs of lines
have a common point |
All pairs of lines
have a common point |
| Coordinates
Analytic/Algebraic |
Ordinary coord's
w/ infinite (ideal) points Homogeneous Coordinates |
Homogeneous Coordinates
with coefficients in {0,1}= Z 2 |
Homogeneous Coordinates
with real number coefficients |
| Transformations
Isometries Similarities |
Similarities | ? | perspective and projective transformations. |
| Harmonic Relation of 4 points on a line. [This will be
the chief tool used to introduce (homogeneous) coordinates into projective
geometry.]
Four points on a line l are harmonically related if the line is determined by a pair of points from the interection of lines in a complete quadrangle and the intersection of that line with the other two sides of the complete quandrangle. [In the figure: The line XZ would determined two other points, XZ#AD=R and XZ#BC=S, so that the points XRZS are harmonically realted.] This would be denoted H(XZ,RS). Four points on a line that are harmonically related: Using the text notation we can show that if H(AB,CD) then H(BA,CD), and also conversely if H(BA,CD) then H(AB,CD). This is the meaning of saying "H(AB,CD) is equivalent to H(BA,CD)". Similarly we can show H(AB,CD) equiv. to H(AB,DC) and H(BA,DC). One way to see this is two envision relabeling the original quadrangle to reverse the order in which the points on the line are organized. |
 |
One key issue then is:
Is the point constructed from the points A,
B and C uniquely determined by the fact that it is in the harmonic relation
with A, B, and C? That is, if A,B, and C are three points
on a line and D and D* are points where H(AB,CD) and H(AB,CD*), then must
D=D*?
This is the question of the uniqueness of the point D. We can prove
that in fact the point D is uniquely determined.
4/23 The
proof follows the argument of Meserve and Izzo.
It used Desargues' theorem several times.
There was a discussion of the dual concept of a harmonic relation between
four lines passing through a single point.
Theorem: If A,B,C, and D are on a line l with H(A,B,C,D)
and O is a point making a section with these four points, consisting of
the four lines a,b,c and d, then H(a,b,c,d).
Proof: see M&I Theorem 5.4.
Corollary: (By Duality) If a,b,c, and d
are on a point O with H(a,b,c,d) and l is a
line making a section with these four lines, consisting of the four points
A,B,C and D, then H(A,B,C,D).
Application:
We can think of a perspectivity between points ABCD on line l
and A'B'C'D' on the line l' with respect to the point O as
being a section of the points ABCD by the point O followed by a section
by the line l' of the lines a,b,c, and d on the point
O.
Applying the previous theorem and its corollary we see that: If
H(AB,CD) then H(ab,cd) and thus H(A'B',C'D').
Note: This application shows that if four harmonically related points
on a line are perspectively related to four points on a second line, then
the second set of four points is also harmonically related. Furthemore,
this result can be extended easily to points that are projectively related.
Thus the transformations of projectivity in projective geometry
preserves the harmonic relationship between four points.
[This last note is comparable to the fact that in Euclidean geometry,
isometries preserve length, and in affine geometry that similarities preserve
proportions.]
In many ways this gives a transformation of the point on the line to
other points that is similar in its nature to reflections and inversions.
Notice that on a projective (affine) line two point will cut the line into
two disjoint pieces, as does a single point for reflection and the points
PR and P-R for inversion, where the transformation
maps points in one set into the other while leaving the "boundary points"
fixed.
With the existence and uniqueness of the point D established, we can
now consider some examples illustrating how to establish a coordinate
system for a projective line by choosing three distinct points to be P0,
P1, and P¥.
We can construct P2, P-1, P1/2, (in two different ways).
Exercise: Construction P3 and P1/3.
Show that with the choice of three points on a projective line
we can construct points using harmonics to correspond to all real numbers
(as in our informal treatment of the affine line).
We will see how this transformation is completely determined by the correspondence of three distinct pairs of points. In some cases the transformation transforms an ordinary point to an ordinary point, the ideal point to an ordinary point and an ordinary point to the ideal point, and in some cases the transformation will transform the ideal point to the ideal point.
A transformation that transforms the ideal point to the ideal point
is called an affine transformation. The composition of two affine transformations
is an affine transformation. The inverse of an affine transformation is
an affine transformation and clearly the identity transformation is an
affine transformation, so the affine transformations are also a group under
the operation of composition (matrix multiplication).
Central Similarities at (0,0) by a factor of M.
Reconstruction of a point on a conic from Pascal's Theorem.
The following materials are from previous course notes and have not been incorporated into the current course notes.
Consider lines connecting corresponding points in a pencil
of points on a line related by a projectivity (not a perspectivity) and
noticed that the envelope of these lines seemed to be a conic, a line
conic. Notice briefly the dual figure which would form a more
traditional point conic. [Also notice how line figures might be related
to solving differential equations e.g. dy/dx=2x-1 with y(0)=3 has a solution
curve determined by the tangent lines determined by the derivative: y=x^2-x+3
which is a parabola.]
In discussing the issue of whether the 5th axiom could be proven from the other four axioms, we looked at an example of another axiom system, with an axiom N (any pair of lines having at one point in common) and an axiom P (given a line l and a point P not on that line there is a line m where P is on m and m and l have no common points) which is a version of the parallel postulate (Playfair's - not Euclid's). We gave examples showing that the four axioms and P were possible as well as the four axioms and N were possible. This showed that one can not prove axiom P or N from the other four axioms since P and N are contradictory.
By a similar analysis of the axioms for the seven point geometry we showed that it not possible prove the 5th postulate from the other four. The analysis examines the example of the seven point geometry and notices that by including an 8th and 9th point the resulting geometry would satisfy the other 4 axioms.
The model we have for affine geometry still satisfies the parallel
postulate, since the ideal (infinite) points of affine geometry are not
considered as ordinary points of the geometry. However, be removing this
distinction between ordinary and ideal points and considering the geometry
that results we obtain a geometry in which there are no parallel lines.
(A projective plane.) This will be a major focus of discussion for the
remainder of the term- especially using the homogeneous coordinates to
consider points in this geometry from an analytic/algebraic approach.
An examination of the problems of transferring an spatial image of a plane to a second plane using the idea of lines of sight we arrived at an understanding of how points in the plane would correspond to lines through a point (the eye).
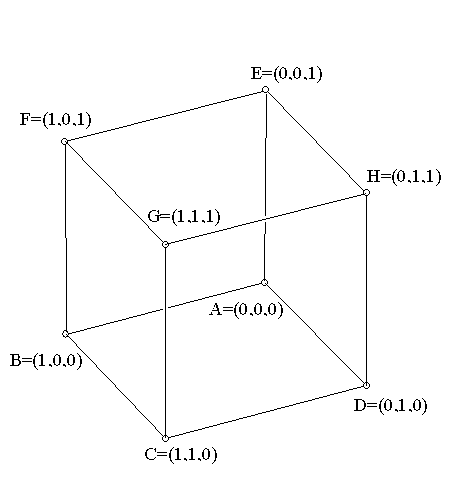
In discussing the 7 point geometry we visualized it using vertices of a cube (besides (0,0,0)) with their ordinary coordinates in standard 3 dimensional coordinate geometry and identified the 7 points . This allowed us to identify "lines" using the homogeneous coordinate concepts and their relation to planes in three dimension through (0,0,0). We identified all but one of the lines easily- the last plane has ordinary equation X + Y + Z = 2... but in this arithmetic for {0,1} we have 1+1=0, so 2=0 and the vertices of that satisfy this equation in ordinary coordinates {(1,1,0), (1,0,1),(0,1,1)} form a line as well.
We then discussed using {0,1,2} for homogeneous coordinates connected
to the arithmetic given by the tables
| + | 0 | 1 | 2 | * | 0 | 1 | 2 | |
| 0 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 2 | 0 | 1 | 0 | 1 | 2 | |
| 2 | 2 | 0 | 1 | 2 | 0 | 2 | 1 |
[Moved from earlier: The lab time was spent working on sketches showing ways to understand that result of the CAROMS film about the inscribed triangles of minimum perimeter.In Lab: Discuss some visual features such as trace and animation and start to look at the use of coordinates. We'll do more with coordinates, along with the use of traces and locus to see some aspects of coordinate geometry next week.]
We also watched the film on projective generation of conics which
introduced Pascal's theorem and its converse about hexagons inscribed in
a conic and showed how to use this result to construct a conic curve passing
through any 5 points. This work was also related to projectivities between
pencils of lines. We will be considering this further in the course. After
a short break we continued using metric ideas to construct an ellipse
as a locus on sketchpad and discussed how to do a parabola as well. By
next Thursday students should construct examples of the three conics on
sketchpad using metric ideas.
| a | b |
| 0 | 1 |
| +/-1 | b |
| 0 | 1 |
We spent the remainder of the lecture time going over the proof of Brianchon's Theorem using the proof of Hilbert and Cohn-Vossen based on hexagons lying on the surface of an elliptic hyperbaloid (which is a ruled surface).