Chapter IX: DIFFERENTIAL EQUATIONS AND POLYNOMIALS: TAYLOR'S THEOREM
© 2000 M. Flashman

In numerous cases throughout this book, as in the real world, we find problems where an exact numerical answer is either impossible or impractical to express as a decimal number. Examples of these situations include calculation of `sqrt{2}, pi, e` , and `ln(2)`. As we have seen there are many ways to characterize and define these numbers and use these characterizations to find an estimate. For our discussion in this chapter it is important to notice that each of these numbers can be characterized as arising from the evaluation of a function which is the solution to a differential equation.Euler's method is one way we have studied to make these estimates.  [See Table 1 below.]


NUMBER
FUNCTION
DIFFERENTIAL 
EQUATION
$\sqrt{2}= f(2)$
$f(x) = \sqrt{x}$
`f ' (x) = 1/ {2f (x)}, f (1) = 1` 
`ln(2) = f(2)`
`f(x) = ln(x)`
`f ' (x) = 1/ x, f (1) = 0`
`e = f(1)`
`f(x) = e^x`
`f ' (x) = f (x), f (0) = 1`
`pi = f(1)`
`f(x) = ` 4arctan` (x)`
`f ' (x) = 4/{1 + x^2}, f (0) = 0`
  • We have discussed approximations from the very beginning of our work on the derivative, with Newton's method for estimating the roots of equations, Euler's method for estimating particular solutions to differential equations, and numerous methods for estimating definite integrals. In the following sections we will delve further into the nature and applications of polynomial approximations based on information about the derivatives of a function.
  • We shall refer to these polynomial approximations as Taylor's approximation theory. To provide further motivation let's consider first a simple situation where an exact value for a function is attainable but perhaps not worth the effort.


    • EXAMPLE IX.A.1: Suppose  `f (x) =x^2 + x^3  + x^100` and we wish to find `f (0.5)`.

    Of course the exact answer is `.25 + .125 + (.5)^100`, but if we only need an estimate of the answer it is easy to settle for .375. The error we make in using this estimate is relatively small [namely `(.5)^100`]. In this example we should note two things.


    Taylor's Theory-Objective and Key Ideas: The main concerns of Taylor's theory for estimating function values are

    1. to find estimating polynomials for a given function and
    2. to measure the error in using these polynomials to estimate the desired values for the given function.
    Two Key Ideas: You may recall from our earlier discussions of estimations using the differential that when `x` is close to `a, f(x)` is approximately equal to a linear function, `f(a) + f '(a) (x-a)`. Furthermore, the Mean Value Theorem guarantees that as long as `f `is a sufficiently well behaved function there is some `c` between `a` and `x` where `f(x) - f(a) = f '(c)(x-a)`. Thus the difference between the function's value at `x` and `a` can be measured using the value of the derivative of `f` at `a`..

    Taylor's theory generalizes these two ideas that use the derivative to estimate.

    IX.A. Estimating `e^x` with Polynomials: An Introduction to Taylor's Theory.

    To focus our discussion more specifially, in this section we will consider only  `f(x)=e^x`and begin by trying to estimate `f(1)=e` illu strating the key ideas of Taylor's theory.
    At `x = 0`, we find that `f(0) =1`, `f '(0) =1`, and since `f '(x) = f(x)` we have that `f^{(n)}(0) =1` for all natural numbers `n`. We now consider our first result, typical of the Taylor's theory approach to estimation using polynomials and derivative information.

    PROPOSITION IX.A.1: If  `P_n(x)= 1 + x+ {x^2}/2 + {x^3}/{2*3} + {x^4}/{4!}+...+{x^n}/{n!}` then
    `P_n(x)` is a polynomial of degree n so that `P_n(0)= P_n'(0)=P_n''(0)=...=P_n^{(n)}(0)=1` and `P_n(b)` is approximately equal to `e^b`.
    In fact, if we let `R_n = e^b - P_n(b)`, then for some `c` between `0` and `b`, `R_n = e^c {b^{n+1}}/{(n+1)!}` .

    GeoGebra: Table, Graph, and Mapping Diagram of `P_n(x)` and `R_n(x)`
     

    Estimating e: Before we proceed to justify this result, we'll apply this result using `n=5` to estimate the value of `e [=e^1]`.
    First, `P_5(x)= 1 + x+ {x^2}/2 + {x^3}/{2*3} + {x^4}/{4!}+{x^5}/{5!} = 1 + x+ {x^2}/2 + {x^3}/{6} + {x^4}/{24}+{x^5}/{120}` , so according to the proposition, `e` is approximately equal to `P_5(1)=1 + 1+ {1^2}/2 + {1^3}/{6} + {1^4}/{24}+{1^5}/{120} ~~ 2.716667` and `R_5 = e-P_5(1)` where `R_5 = e^c {1^6}/{6!}=e^c 1/720` for some `c` between `0` and `1`. Thus, `e` is approximately `2.716667` and the error in using this estimate is `R_5`. Since `c` is between `0` and `1`, `e^c` is between `1` and `e`, so we can deduce that `R_5`, the difference between e and the estimate, `P_5(1)`, is no greater than `e/720`. Using estimates of `e` from our earlier work in Chapter VI we know that `e< 3` so our error `R_5(1)` is no larger than `3/720 = 1/240 \approx 0.004167`.This compares roughly well with the error from the GeoGebra applet that shows an error after setting the slider $n = 5$ to  find `R_5(1) = 0.00162`.

    A more accurate estimate can be obtained by using a larger value for `n`. Try using `n=6` and `7` to see the improvement. [This can be done progressively using the GeoGebra  applet above or download a spreadsheet which you can examine now or later.]

    Proof of Proposition: We'll begin our proof by finding `P_n'(x)`.

    `P_n'(x)=1+ x+{x^2}/2 +{x^3}/{2*3}+{x^4}/{4!}+...+{nx^{n-1}}/{n!}`
    `= 1 + x+ {x^2}/2 + {x^3}/{2*3} + {x^4}/{4!}+...+{x^{n-1}}/{(n-1)!}=P_{n-1}(x)` 

    From this it follows easily that  `P_n(0)= P_n'(0)=P_n''(0)=...=P_n^{(n)}(0)=1`.

    Now suppose that `b` is not  `0` and let `R_n = e^b - P_n(b)`.
    We need only justify the formula for evaluating `R_n`. For convenience we'll write `R=R_n` and let

    `g(t) = e^t P_n(b-t) + R{(b-t)^{n+1}}/{b^{n+1}}`.
    Then `g(b) = e^b P_n(b-b) + R{(b-b)^{n+1}}/{b^{n+1}}= e^b P_n(0) = e^b` , while
    `g(0) = e^0 P_n(b-0) + R{(b-0)^{n+1}}/{b^{n+1}}=P_n(b) + R = e^b` from the definition of R.

    Furthermore `g'(t) = e^t P_n(b-t) - e^t P_n'(b-t)-R{(n+1)(b-t)^{n}}/{b^{n+1}}=e^t[P_n(b-t) - P_n'(b-t)]-R{(n+1)(b-t)^{n}}/{b^{n+1}}`

     But `P_n(x) - P_n'(x) = {x^n}/{n!}`, so`g'(t) = e^t {(b-t)^n}/{n!}-R{(n+1)(b-t)^{n}}/{b^{n+1}}`.

    Now we apply the Mean Value (or Rolle's) Theorem to the function g, we can say that there is a number `c` between `0` and `b` where `g'(c)=0`. Thus 
    `0 = e^c {(b-c)^n}/{n!}-R{(n+1)(b-c)^{n}}/{b^{n+1}}`and  `e^c {(b-c)^n}/{n!}= R{(n+1)(b-c)^{n}}/{b^{n+1}}`. Solving this last equation for R gives
    `R_n = R = e^c {b^{n+1}}/{(n+1)!}`.

    EOP.

    Note: Since the exponential function has a positive derivative for all `x`, the function is increasing for all `x`.
    (i) If `0<c<b` then `1< e^c < e^b < 3^b` and `0 < {b^{n+1}}/{(n+1)!} < R_n = R = e^c {b^{n+1}}/{(n+1)!} < e^b {b^{n+1}}/{(n+1)!}< 3^b{b^{n+1}}/{(n+1)!}`.
    (iia) If `0>c>b` then `1> e^c >e^b > 2^b` and if `n` is odd then `{b^{n+1}}/{(n+1)!` is positive and thus `{b^{n+1}}/{(n+1)!} > R_n = R = e^c {b^{n+1}}/{(n+1)!} > 2^b {b^{n+1}}/{(n+1)!} > 0`.
    (iib) If `0>c>b` then `1> e^c >e^b > 2^b` and if `n` is even then `{b^{n+1}}/{(n+1)!` is negative and thus `{b^{n+1}}/{(n+1)!} < R_n = R = e^c {b^{n+1}}/{(n+1)!} < 2^b {b^{n+1}}/{(n+1)!} < 0`.
    Putting this information about the quality of `R_n` together we can see the following:
    For all `x > 0` and for any `n`, `e^x > P_n(x)`,
    while for ` x< 0` the polynomials differ in relation to `e^x`:
    When `n` is odd then `e^x > P_n(x)`;
    when `n` is even then `P_n(x) > e^x`.

    Estimating the value of e is not the only use for the previous proposition. Before turning to the more general Taylor's theory in the next section, here are two more examples of its application in estimating definite integrals related to ex.

    EXAMPLE IX.A.2: Estimate `int_0^1 e^x dx = e-1`. Use this to estimate `e`.

    Solution: Using Proposition IX.1 with `n=4` for each x between `0` and `1` we have
    `0<e^x =P_4(x) + R_4(x) = 1 + x+ {x^2}/2 + {x^3}/6 + {x^4}/24+R_4(x)` where `R_4(x) = e^c {x^5}/120`
     for some `c` with `0<c<x<1`.

    Thus`0<R_4(x)<3 {x^5}/120 = {x^5}/40`. [Remember `e^c<3`.] and so `P_4(x)<e^x<P_4(x) + {x^5}/40` for all `x` between `0` and `1`. Now we use the monotone property of the definite integral [Ch. V . ** ] to obtain the estimate:
    `int _0^1P_4(x)dx<int_0^1e^x dx<int_0^1P_4(x) + {x^5}/40`, so

    `1+1/2 + 1/6+1/24+1/120< e-1<1+1/2+1/6+1/120+1/240`.

    Therefore `e` is approximately `1 + 1+ 1/2+1/6+1/24+1/120 ~~2.716667` as in the first estimate we saw in the note after the statement of the theorem, and the error in using this estimate is less than `1/240` as we also saw previously.

    The next example follows a similar analysis but applied to a more difficult yet important integral for probability and statistics.

    EXAMPLE IX.A.3    : Estimate `int_0^1 e^{-t^2}dt`.

    Solution: For each `t` between `0` and `1`, `-t^2` is between `-1` and `0`. Let `x = -t^2`. By Proposition IX.1 with `n = 4` for each `x` between ` -1` and `0` we have

    `0<e^x =P_4(x) + R_4(x) = 1 + x+ {x^2}/2 + {x^3}/6 +{x^4}/24+R_4(x)`
    where `R_4(x) = e^c {x^5}/120` for some `c` with `0>c>x`.

    Since `c<0` , `0<e^ c<1`, and since `x < 0` we have that  `0>R_4(x)>{x^5}/120`.





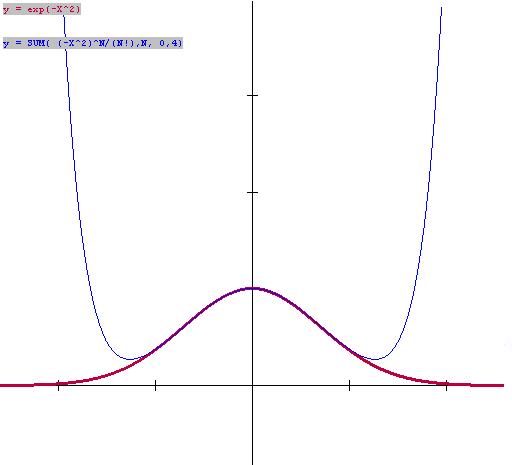
    GeoGebra Estimates for  `int_0^1 e^{-t^2}dt`. Check off box to show estimate.

    Substituting `-t^2` for `x` ,we see that

    `e^{-t^2} = 1 + (-t^2)+ {(-t^2)^2}/2 + {(-t^2)^3}/6 +{(-t^2)^4}/24+R_4(-t^2) = 1-t^2+{t^4}/2 -{t^6}/6 +{t^8}/24 + R_4(-t^2)`  

    Now since `0>R_4(-t^2)>{(-t^2)^5}/120 ={-t^10}/120` we have `int_0^1 P_4(-t^2)dt >int_0^1 e^{-t^2} dt > int_0^1 P_4(-t^2) -{t^10}/120 dt`.

    By evaluating these integrals we obtain

    ` int_0^1 1-t^2+{t^4}/2 -{t^6}/6 +{t^8}/24 dt > int_0^1e^{-t^2}dt > int_0^1 1-t^2+{t^4}/2 -{t^6}/6 +{t^8}/24 - {t^10}/120 dt`

    or `1- 1/3 + 1/10- 1/42+ 1/216 > int_0^1e^{-t^2}dt > 1 - 1/3 + 1/10- 1/42+ 1/216 - 1/1320`

    Therefore, `int_0^1 e^{-t^2}dt` is approximately equal to `1 - 1/3 + 1/10 - 1/42 + 1/216 ~~ 0.747486...`;

    and this is an overestimate by no more than `1/1320`.

    Comment: In both of these examples we have been able to estimate a definite integral involving the exponential function by using a Taylor polynomial of degree 4. It should be apparent that by using a higher degree for the estimating polynomial, the error term will become smaller and we will obtain a more precise estimate. The systematic pattern in these polynomials should allow you to find more precise estimates for the last example without much difficulty.

    Go on to Chapter IX.B

    Exercises IX.A.:
    1. Use the Taylor polyonmial for `e^x` of degree `4` to estimate the following:

      2. (a) `e^2` (b) `e^3` (c) `e^.5` (d) `e^-1` (e) `e^3.14`. [Use GeoGebra or  Spreadsheet helper.]
    2. Estimate e using the Taylor polynomial of degree n where n is (a) 6 (b) 7 (c) 8 (d) 10.

      3. In each of these estimates discuss the size of the error term Rn.  [Use GeoGebra or  Spreadsheet helper.]
    3. What value of n should be used so that the Taylor polynomial of degree n will give an estimate of e that is within .000001 of the exact value of e? Explain your result using Proposition XI.A.1
    4. Use the Taylor polynomial for ex of degree 5 to estimate `int_0^1 e^{-t^2}dt`. Discuss the error in this approximation.
    5. Use the trapezoidal rule and Simpson's rule with n = 6 to estimate `int_0^1 e^{-t^2}dt` .
    6. Use the Taylor polynomial for `e^x` of degree 6 to estimate `int_0^1 e^{-t^2}dt`. Discuss the error in this approximation.
    7. On the same graph sketch the graph of `e^x` along with those for the Taylor polynomials for `e^x` of degree 1,2,3,4 and 5. [You can do this by use the trace feature on the graph of `P_n` in the GeoGebra applet.] Discuss the graphical interpretation of `R_n`. [Here is Java sketch solution for n = 1 to 5]
    8. What value of n should be used so that the Taylor polynomial of degree n will give an estimate of  `int_0^1 e^{-t^2}dt` that is within `0.000001` of the exact value? Explain your result.
    9. Use the Taylor polynomial for `e^x` of degree 4 to estimate the area of the region in the plane contained by the lines `X=0`, `X=1`, the X- axis and the graph of `y = 1 + xe^{-x}` . [Hint: First find a polynomial to estimate `e^{-x}` .] Discuss the error in this approximation.
    10. Another Polynomial Estimate: Consider the functions `1/{1-x}` and `1/{1+x}`.
      1. Show that `1 = (1-x ) ( 1 + x + x^2+ x^3+x^4+ x^5) + R` where `R =x^ 6` .
      2. Show that `1 = (1+x) ( 1-x + x^2 - x^ 3+x^ 4 - x^ 5) + R` where `R = x^ 6` .
      3. Show that when `0 < x< 1, 1/ (1- x) = ( 1 + x+ x^ 2+ x^ 3+ x^ 4+ x^ 5 ) + R_1` where `R_1 = {x^ 6} /{ 1-x}`
      4. Show that when `0< x < 1, 1/ {1+ x} = ( 1 -x+ x^ 2 - x^ 3+ x^ 4 - x^ 5 ) + R_2 ` where `R_2 = {x^ 6}/{1+ x}`.
      5. Use the definite integral and the previous equations to estimate ln(.9) = ln (1 - .1) and ln(1.1) = ln(1 + .1). [ This approach to estimating the natural logarithm was used by Isaac Newton to give very accurate estimates of ln(2), ln(3), etc.]. Discuss the error in your estimate based on the integrals of R1 and R2.
      6. Generalize this for higher degree polynomials and estimating ln(.8), ln(1.2), ln(.99) and ln(1.01).