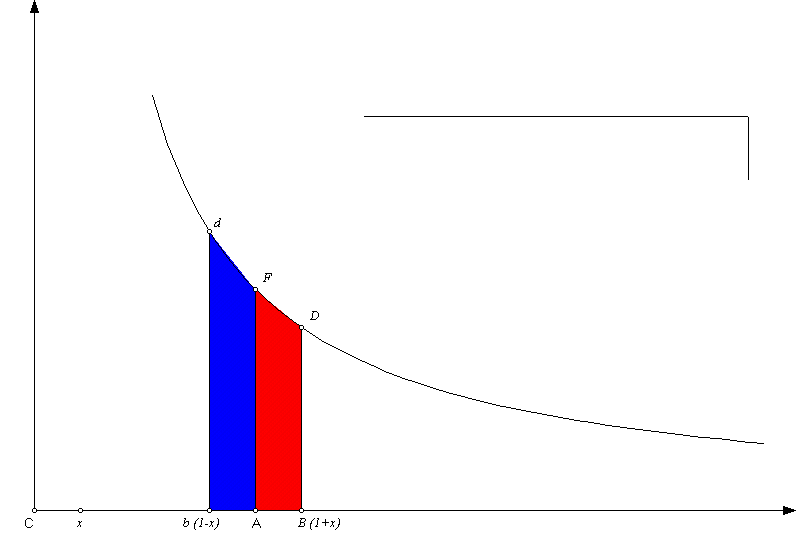
Notes on Newton's estimates for the Hyperbolic Logarithm.

Newton considers symmetrically located points on the main axis, 1+x and 1-x with x>0 and their related reciprocals.
He then uses two integrals related to the geometric series to determine the related areas,
(i) between the hyperbola and above the segment [1,1+x] (red) and
(ii) between the hyperbola and above the segment [1-x, 1] (blue):

(i)
(ii)

These allow the estimation of the sum and difference of the two areas:


.

Now Newton uses the first eight terms with h = .1 (and .2) to estimate the hyperbolic log of .9, 1.1 (.8 , and 1.2).

[Tables created with Microsoft Excel]


h 0.1 .2 .01
2h 0.2 0.4 0.02
2h3/3 0.000666666666666 0.00533333333333 0.00000066666666667
2h5/5 0.000004 0.000128 0.00000000004
2h7/7 0.0000000285714286 0.00000365714285714 0.00000000000000286
2h9/9 0.0000000002222222 0.00000011377777778 2.22222222222e-19
2h11/11 0.0000000000018182 0.00000000372363636  
2h13/13 0.0000000000000154 0.00000000012603077  
2h15/15 0.0000000000000001 0.00000000000436907  
Sum of Areas 0.200670695462151 0.405465108108002 0.020000666706670
h 0.1 .2 .01
h2 0.01 0.04 0.0001
h4/2 0.00005 0.0008 0.000000005
h6/3 0.0000003333333333 0.00002133333333 0.000000000000333
h8/4 0.0000000025 0.00000064 2.50000000000e-17
h10/5 0.00000000002 0.00000002048  
h12/6 0.0000000000001667 0.00000000068267  
h14/7 0.0000000000000014 0.00000000002341  
Diff'ce of Areas 0.010050335853501 0.040821994519406 0.000100005000333
Now to find the Area of the two separate regions (and related logarithms) we take 1/2 of the difference of these results and 1/2 of the sum of these results.

Thus ln(1.1)= 1/2 ( 0.2006706954621511- 0.0100503358535014)

= 0.0953101798043248

while ln(.9) = -(1/2)( 0.2006706954621511 + 0.0100503358535014)

= -0.105360516578263 .

And ln(1.2)= 1/2 (0.405465108108002 -0.040821994519406 )

= 0.18232155576939546 (from Newton)

while ln(.8) = -(1/2)(0.405465108108002 +0.040821994519406 )

= -0.2231435513142097 (from Newton) .

Newton can also find ln(1.01) and ln(.99) by using h=.01 from the same tables.
 

Then Newton finds other logarithms with great accuracy using these.

For Example:

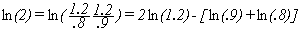
= (approx) 2(0.18232155576939546) +0.105360516578263+ 0.2231435513142097

= 0.6931471805599453 (from Newton)