Section I.C. OTHER ESTIMATING CONTEXTS (draft)

Throughout the remainder of this book estimating a value of some quantity will be a recurrent theme as it has been throughout the history of mathematics. In Sections I.C.1 and I.C.2 we'll examine two more subject areas of both historical and current importance that were introduced in Section 0.C, probability and economics. In these subjects estimations of the type investigated with tangent lines and instantaneous velocity are also relevant.If you are anxious to reach the mathematical concepts that these models (along with those of Sections I.A and I.B) motivate you may proceed now directly to section I.D. However, be sure to cover this section before proceeding to Chapter II, as these models will serve as interpretations for some of the later results in the text.


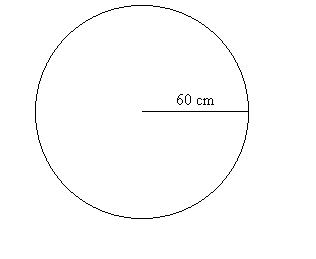
I.C.1 Probability Distributions and Density. In Section 0.C (which you might want to review now), we introduced some basic concepts of probability with the darts model. To explore these ideas further we'll continue our examination of that model. Recall that we were considering a circular magnetic board of radius sixty centimeters. This magnet is very strong and uniformly attracting so that when I turn my back to it and release a magnetic dart, the dart will be drawn to the board and is equally likely to land on any point on the board. This is our basic experiment. After performing the experiment we measured the random variable $R$, the distance from the dart to the center of the circle.
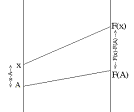
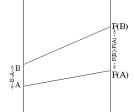
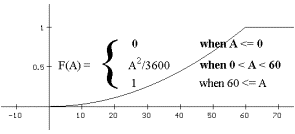
Notation: As in Chapter 0.C we will denote the probability that the random variable $R$ has a value less than or equal to $A$ by F($A$) where $A$ is any real number. F is a function of $A$ called the (cumulative) probability distribution function for the random variable $R$. When analyzed by cases we saw that $ F($A$) = \begin{align} 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A\le0 \\ \frac {A^2}{3600}\ \ \ \ \ \ \ \ \ 0 \lt A \lt 60 \\ 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 60 \le A \end{align}$ . See Figures * and * for a mapping diagram and graph of this function.


.

We also saw in Section 0.C that the probability of the random variable $R$ being precisely any specified value is always $0$. A related and important issue is how to measure the likelihood of the dart landing close to or equal to a particular distance, $A$, from the center of the dart board. To be more specific, how can we measure the likelihood that the value of $R$ would be close to or equal to $A=50$ centimeters? And can we compare this to the likelihood that the value of $R$ would be close to or equal to $A=10$ centimeters? The actual probability of these events depends on the value of $A$ and the length of the interval that is considered "close" to $A$.

Example I.C.1.For our discussion, let's consider the dart falling close to 50 centimeters from the center as meaning that $R$ is in the interval [49,51], and falling close to 10 centimeters as having $R$ in the interval [9,11]. The probabilities for $R$ being in these intervals is computed as in Section 0.C:

F(51) - F(49) = 51²/ 3600 - 49²/3600 = 200 / 3600 = 1/18 for the interval [49,51], and F(11) - F(9) = 11²/ 3600 - 9²/ 3600 = 40 / 3600 = 1/90 for the interval [9,11]. These measurements do not resolve the dart issue very well since the probabilities change with the choice of the intervals used to determine what "close" means. (What if we had used the interval [49.9,50.1]? ) To resolve the issue of relative likelihood of the dart falling a certain distance from the center, we will develop the concept of point probability density.


Point Probability Density: Recall from Section 0.C that the average probability density (APD) of a random variable $R$ for an interval [A,B] is the ratio of the probability that A< $R$ < B to the length of the interval $[A,B]$, i.e., $APD(A<B)=\frac {F(B)-F(A)}{B-A}$

So the APD of $R$ in the interval $[29,31], APD(29,31) = (1/18)/2 = \frac1 {36}$ and for the interval $[9,11]$ the $APD(9,11)= (1/90)/2 = \frac 1{180}$

Definition: The (point) probability density (PD) of a random variable $R$ for a value $A$, denoted $f (A)$, measures the likelihood that $R$ will take a value close to $A$. This number is estimated by average probability densities for very short intervals with $A$ as one endpoint.
Let $\overline f(x)=\frac {F(x)-F(A)}{x-A} = APD(x,A)$, the APD for $R$ on an interval with endpoints $A$ and $x$ where $x$ is different from $A$. The preceding statements can be expressed by saying that as $x$ approaches $A$, the values of $\overline f(x)$ should approach $f (A)$, i.e., as $x \rightarrow A$, we should find that $\overline f(x) \rightarrow f(A)$.

Note: This method is very similar to the way that average velocities for very short time intervals estimate the instantaneous velocity of a moving object, or that the slope of a secant line for a short interval estimates the slope of the tangent line to a curve.

We'll continue the example that illustrates the meaning of this by determining the point probability density of $R$ for the values $A=50$ cm. and $A = 10$ cm. [You might pause a minute here and make your own estimates for these numbers.]

EXAMPLE I.C.1. (Cont'd.) In the darts experiment described above and in Example 0.C.3 with the random variable $R$, we find the average probability density for $R$ for the intervals $[49,50]$ and $[50,51]$ to estimate the point probability of $R$ at $50$ cm.
Using the probabilities from the previous discussion, we find the average probability density for $[49,50]$, $APD(49,50)= 99/3600 = 11/400$, while the $APD(50,51) = 101/3600$.

We continue to examine more closely the APD for intervals with 50 as an endpoint in an attempt to determine whether some number can be assigned as a point probability density to the number 50. Figure I.17 shows a table of APD's for intervals with one endpoint being 50.

Figure I.17
Table of APD's for intervals with one endpoint being 50


Interval	Average Prob.Density
[49,50]	99/3600
[49.9,50]	99.9/3600
[49.99,50]	99.99/3600
[50,51]	101/3600
[50,50.1]	100.1/3600
[50,50.01]	100.01/3600

Letting $\overline f(x)=$ the APD for $R$ on an interval with endpoints 50 and $x$ where $x$ is different from 50, we have that $\overline f(x) = [ x^2/3600 - 2500/3600] / [x -50]$ $= [(x+50)(x-50)] /[3600 (x-50)]$
$= [x + 50]/ 3600$ . Thus as $x \rightarrow 50, \overline f(x) \rightarrow \frac1{36}$ and we can say that at $A$ = 50 the random variable $R$ has a (point) probability density of $\frac1{36}$, or $f (50) = \frac1{36}$.
Similar analysis of APD's for intervals with endpoint 10 leads to a finding that $R$ has a (point) probability density at $A= 10$ of $1/180$ or $f (10)= 1/180$. The higher probability density for $50$ in some sense explains why the value of $R$ - which measures the distance of the dart from the center of the dart board- is more likely to be closer to $50$ than to $10$.

Comment: It is left for the reader to find a formula for the point probability density of $R$ for $A$ with $0 < A < 60$, i.e., a formula for f$ (A)$. [See Exercise 2.]

Exercises I.C.1. For related problems on probability distributions and average probability density see Exercises 0.C.
1. For the random variable $R$ of Example I.C.1 find the point probability density for 20. Find the point probability for 40. Explain briefly why you would expect $R$ to be close to 40 more likely than it would be close to 20.

2. For the random variable $R$ of Example I.C.1 find the point probability density for $A$ where 0 < $A$ < 1 .

Dart Boards with Different Shapes.
3. Suppose the dart board for our experiment is a 3' by 5' rectangle and when the dart lands we report the distance of the dart to the 5' side with the random variable L. [See Figure I.18]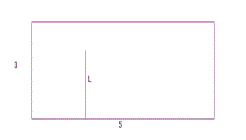
a. Find the point probability density for L at 1.
b. Find the point probability density for L at $A$ with 0 < $A$ < 3.

4. Suppose the dart board is a right triangle with legs 3' and 4' and when the dart lands we report the distance of the dart to the 4' side with the random variable H. [See Figure I.19]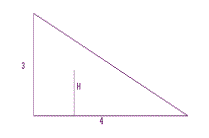
a. Find the point probability density for H at .1.
b. Find the point probability density for H at $A$ with 0 < $A$ < 3.

5. Suppose X is a random variable which takes values in the interval [0,2] and that for each of the following definitions of F, F($A$) gives the probability that X $A$ where 0<$A$<2.
i. Find the (point) probability density of the distribution for X at 1.
ii. Find the (point) probability density of the distribution for X at $A$ where 0 < $A$ < 2.
a. F(A) = .5 A. b. F(A) = 1/4 A ². c. F(A) = A² - 3/2 A.
d. F(A) = 1/8 A³ . e. F(A) = 1/16 A⁴.

6. Suppose F(A) = sin(A) describes the probability that a random variable Y is less than or equal to $A$ where 0 < A < π /2. Using your calculator estimate the point probability density for Y at π/4 using the intervals [ π/6, π/4] , [π /4, π/3], and [π /4, π /4 + .1]. Discuss briefly what you think the point probability density for Y at π /4 might be. [See problem 11 in section 0.C.]

7. Suppose that an object is inside a sphere of radius 10 centimeters and it is equally likely that it is at any point in the sphere. Let $R$ denote the random variable that measures the distance from the object to the center of the sphere. [See problem 12 in section 0.C.]
Why is the probability that $R$ <= A with A < 10 given by A³/1000? Find a formula for the point probability density for $R$ at $A$ with 0 <$A$ <10.

8. In Example I.C.1 consider the average probability density for intervals of the form [x,60] and [60,x]. Discuss the issue of whether there is a point probability density for $R$ at $A$=60 based on some calculations for these intervals.

9. Another Darts Board. Suppose the dart board has a shape bounded by the polygon in Figure *** in the coordinate plane and when the dart lands we report the first coordinate of the point measuring the distance of the point to the Y axis with the random variable X.

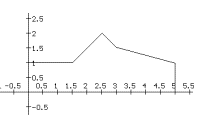
a. Draw a mapping diagram and sketch of what the cumulative distribution function F for X might be, based on the figure, i.e., the function F where F(A) is the probability that $X \le A$.
b. Estimate the point probability density for X at $A$ = 1, 2, 3, and 4..
c. Find the point probability density for X at $A$ with 0 < $A$ < 5.

10. Point Probability Density and The Tangent Problem. Write a comparison of the treatment of point probability density to the solution of the tangent problem. Discuss the following statement in your essay: " The probability density of a random variable X at a point $A$ is measured by the slope of the line tangent to the graph of the cumulative distribution function F at the point $(A,F(A))$."

11. Project on Estimation and Archimedes: The Greek mathematician and scientist Archimedes (287-212 B.C.E.) wrote perhaps the first work to give a systematic method for estimation. Read On the Measurement of the Circle where Archimedes estimates pi in Proposition 3. Write a paper describing the content and method of this work.