"Revitalizing Complex Analysis" ¤
January 9, 2016
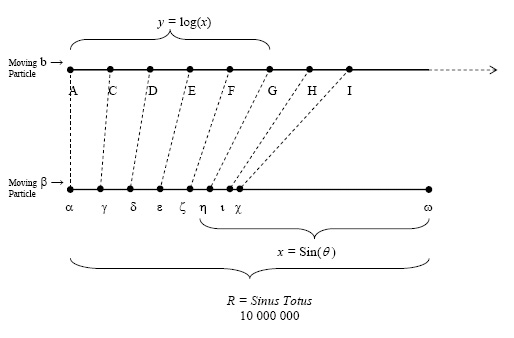
Visualizing Complex Variable Functions with Mapping Diagrams:
Linear Fractional Transformations.
Martin Flashman
Professor of Mathematics
Humboldt State University
http://flashman.neocities.org/Presentations/JMM2016/MD.JMM.CV.1_9_16.3.html