Estimating  Integrals Using Polynomials:

A Tale of Two Problems (and a little history as well)

Algebra Prelude: "Geometric Series"
               (1-x) (1 + x + x2  .... +xn-1 ) = 1 - xn 
So    1/ (1-x) = xn  / ( 1 - x)  + 1 + x + x2  .... + xn-1 
AND   (1+x) (1 - x + x2  .... +(-1)n-1 xn-1 ) = 1 +(-1)n-1 xn 
So    1/ (1+x) =(-1)n-1 xn  / ( 1 - x)  + 1 - x + x2  .... +(-1)n-1 xn-1  
Substitution:
 `int_1^{1+h} 1 / x dx = int_0^h 1 / {1+u} du `;
Use  x = 1 + u
 so    u = x - 1.
----------------------------------------------------------
 `int_{1-h} ^1 1 / x dx = int_0^h 1 / {1-u} du` ;
Use x = 1- u   
so    u = 1-x  and du = - dx .

Problem I : [Newton Estimates for the Natural Logarithm of 2]

What is the area of the region in the plane bounded by
the X-axis, X=1, X=2 and Y = 1/X ?
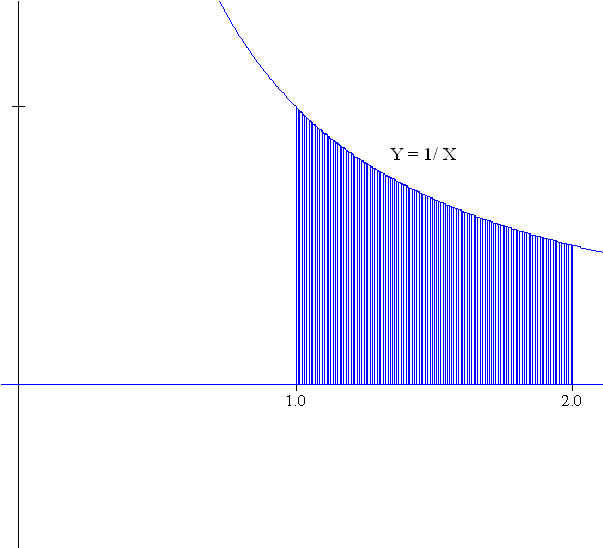
Problem II: Taylor / Maclaurin Polynomial Estimate for An Important Integral from Probability

What is the area of the region in the plane bounded by the X-axis, X=0, X=0 and `Y = e^{-X^2}`?     or  
what is  `int_0^1 e^{-x^2} dx` ?

I. Newton:

In 1676 Isaac Newton wrote in a letter to Henry Oldenburg on some of his applications of polynomials and series to estimating areas. In particular he related how he estimated areas for the natural logarithm which was also called the hyperbolic logarithm in those days.

This work was later clarified in the book Of the Method of Fluxions and Infinite Series which was published posthumously in 1737, ten years after Newton's death.

So... 
A little background on the hyperbolic logarithm:

In 1637, Descartes published  La Geometrie as an appendix to his Discours de la Methode. This started the investigation of geometry using arithmetic and algebra through common measurments, coordinates, and equations that described curves.

By about 1640, the solution to the "area problem" for curves with equation  Y n = aX m  was known by Fermat  for all  integer cases except when n = 1, m = -1.

I.e., the only unsolved area problem was for Y = 1/X  - the standard equation for the graph of a hyperbola.

In 1647, Gregoire de St. Vincent showed the following special property for hyperbolas:

Proposition 1: If a/b = c/d then the area under the hyperbola above the interval [a,b] is equal to the area under the hyperbola above the interval [c,d].


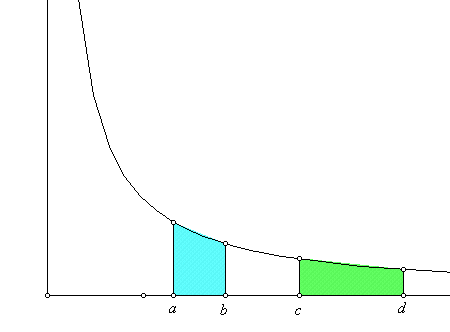
The proof of this may be discussed if time permits. You can try it as an exercise in integration substitution.

In 1649 Alfonso Antonio de Sarasa recognized this feature in Gregoire's work  and connected it to the properties of logarithms.

In particular he recognized the following additive property of these measurements which had previously be a key feature in the study of common logarithms (base 10):

Proposition 2: If the areas are all measured using a = 1, then
the area determined by a product of two numbers , rs,  is equal to the sum of the areas determined by r and s separately.

Here's why:
We can see easily that `1/r =s/{rs}`.
So by Proposition 1  the area under the hyperbola above the interval [1,r] is equal to the area under the hyperbola above the interval [s,rs].

But the area under the hyperbola above the interval [1,rs] can be cut into two pieces above the intervals [1,s] and [s ,rs]. so the area determined by a product of two numbers , rs,  is equal to the sum of the areas determined by r and s separately.

 
From the calculus you've studied you should recognize this area as a definite integral of 1/x  from 1 to r and from the Fundamental Theorem of Calculus, this area is precisely the logarithm base e evaluated at r.
i.e.  `int_1^r 1/x dx  = log_e (r)` 

So we can recognize from what you've learned in calculus that this Natural Logarithm is the same as the logarithm with the base e. But how does one actually find these logarithmic values. For example, how can we estimate the natural logarithm of 2?

Using rectangles or trapezoids or even parabolas to estimate the area is not particularly accurate for estimating ln(2).
Try a quick estimate yourself with n = 10. [Demonstrate with winplot.]
RH: 0.66877   LH: 0.71877   MP: 0.69284

Newton gives this estimate using only 15 simple calculations:
0.6931471805599453

So... How did Newton make estimates for this area that were so very accurate yet easy to compute?

Newton considers the graph of 1/x  and symmetrically located points on the main axis, 1+x and 1-x with x > 0 and their related reciprocals.

Newton is familiar with the "geometric series" so  he knew he could estimate  1/(1-x) and 1/(1+x) with  polynomials.
 

He then uses two integrals related to the geometric series to determine the related areas,
(i) between the hyperbola and above the segment [1,1+x] (red)

P=Area AFDB =
`int_0^h 1/{1+x}dx  = int_0^h 1 - x + x^2 - x^3 +...= h - {h^2}/2 + {h^3}/3 - {h^4}/4 + ...`
and

(ii) between the hyperbola and above the segment [1-x,1] (blue):
Q=Area AFdb =
`int_0^h 1/{1-x}dx  = int_0^h 1 + x + x^2 + ...+ x^{k-1} +...= h + {h^2}/2 + {h^3}/3 + ...+ {h^k}/ k + ...`

These allow the estimation of the sum and difference of the two areas:
T = Total Area of bdDB = Q+P  =  `2h + 2{h^3}/3 + 2{h^5}/5 + 2{h^7}/ 7 + ...`

S = Difference of Areas Ad-AD = Q-P  =  `h^2 + {h^4}/2 + {h^6}/3 + {h^8}/ 4 + ...`
So we can estimate P and Q by :
Q = 1/2 [T+S] and P = 1/2[T-S].

Now Newton uses the first eight terms with h = .1 (and .2) to estimate the hyperbolic log of .9 and 1.1 (as well as .8  and 1.2).

[Tables created with Microsoft Excel]


h 0.1 .2 .01
2h 0.2 0.4 0.02
2h3/3 0.000666666666666 0.00533333333333 0.00000066666666667
2h5/5 0.000004 0.000128 0.00000000004
2h7/7 0.0000000285714286 0.00000365714285714 0.00000000000000286
2h9/9 0.0000000002222222 0.00000011377777778 2.22222222222e-19
2h11/11 0.0000000000018182 0.00000000372363636  
2h13/13 0.0000000000000154 0.00000000012603077  
2h15/15 0.0000000000000001 0.00000000000436907  
T=Sum of Areas 0.200670695462151 0.405465108108002 0.020000666706670


h 0.1 .2 .01
h2 0.01 0.04 0.0001
h4/2 0.00005 0.0008 0.000000005
h6/3 0.0000003333333333 0.00002133333333 0.000000000000333
h8/4 0.0000000025 0.00000064 2.50000000000e-17
h10/5 0.00000000002 0.00000002048  
h12/6 0.0000000000001667 0.00000000068267  
h14/7 0.0000000000000014 0.00000000002341  
Diff'ce of Areas 0.010050335853501 0.040821994519406 0.000100005000333

Now to find the Area of the two separate regions,P and Q, (and therefore the related logarithms) we take 1/2 of the difference of these results and 1/2 of the sum of these results.

Thus ln(1.1)= 1/2 ( 0.2006706954621511- 0.0100503358535014)

= 0.0953101798043248

while ln(.9) = -(1/2)( 0.2006706954621511 + 0.0100503358535014)

= -0.105360516578263 .

And ln(1.2)= 1/2 (0.405465108108002 -0.040821994519406 )

= 0.18232155576939546 (from Newton)

while ln(.8) = -(1/2)(0.405465108108002 +0.040821994519406 )

= -0.2231435513142097 (from Newton) .

Newton can also find ln(1.01) and ln(.99) by using h=.01 from the same tables.
 

Then Newton finds other logarithms with great accuracy using these.
In particular Newton calculates the estimate for 

ln(2) =  ln ( 1.44 / .72) = ln (1.44)-ln(.72) = 2ln(1.2) -[ln(.9 +ln(.8)] 

= (approx) 2(0.18232155576939546) +0.105360516578263+ 0.2231435513142097

= 0.6931471805599453 (from Newton)
WOW!    :)
Here's the way it looked in Newton's book  
Of the Method of FLUXIONS:

Now on to   Problem II: