Problem II: Taylor / Maclaurin Polynomial Estimate for An Important Integral from Probability
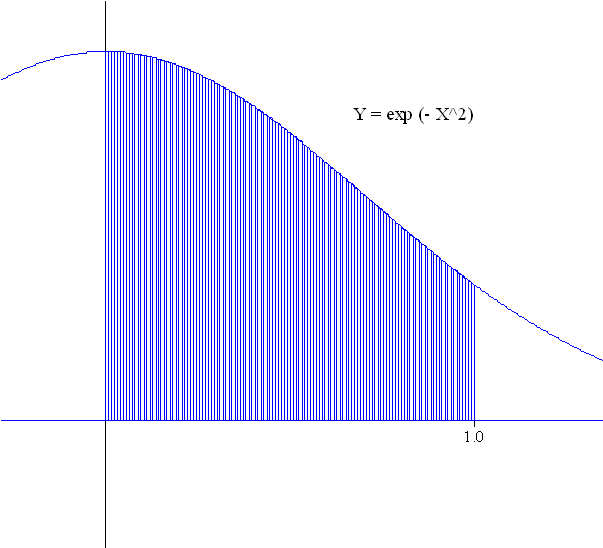
What is the area of the region in the plane bounded by the X-axis, X=0, X=1 and `Y = e^{-X^2}`? or
what is `int_0^1 e^{-x^2} dx` ?
Problem II: Taylor / Maclaurin Polynomial Estimate for An Important Integral from Probability
What is the area of the region in the plane bounded by the X-axis, X=0, X=1 and `Y = e^{-X^2}`? or
what is `int_0^1 e^{-x^2} dx` ?
The key concept is to use information about derivatives to design the polynomial.
At x = 0, we find that f(0) = 1, f '(0) =1, and since
f
'(x)
= f(x) we have that f (n)(0) = 1 for all
natural numbers
n. We now consider the key result, typical of
the Taylor's theory approach to estimation using polynomials based on derivative
information.
THEOREM:
If
`P_n(x) = 1 + x + {x^2}/2 + {x^3}/{2*3) + {x^4}/{4!} + {x^5}/{5!} +...+ {x^n}/{n!} ` then Pn(x) is the unique polynomial of degree n
so that
and Pn(b) is approximately equal to eb.
In
fact, if we let the error in this estimation be denoted by Rn = eb - Pn(b)
[ so eb = Pn(b) + Rn ]
then for some c between 0 and b
To illustrate the key ideas of Taylor's theory, we start by estimating the number e with a polynomial.
Estimating e: We
apply
the theorem using n = 5 to estimate the value of e [= e1].
First,
` P_5(x) = 1 + x + {x^2}/2 + {x^3}/{2*3) + {x^4}/{4!} + {x^5}/{5!} = 1 + x + {x^2}/2 + {x^3}/6 + {x^4}/24 + {x^5}/120 `.
So according to the theorem, e is approximately equal to
and R5 = e - P5(1) where `R_5 = e^c {1^6}/{6!} = e^c 1/720 ` for some c between 0 and 1.
Thus, e is approximately 2.716667 and the error in using this estimate is R5. Since c is between 0 and 1, ec is between 1 and e, so we can deduce that R5, the difference between e and the estimate, P5(1), is no greater than e/720. Using estimates of e from your earlier work we know that e < 3, so our errror R5 is no larger than `3/720 = 1/240`.
A more accurate estimate can be obtained by using a larger value for n. Try using n=6 and 7 to see the improvement. [This can be done progressively using a spreadsheet which you can examine now or later.]
We are now ready to estimate `int_0^1 e^{-t^2} dt`.
Solution: For each t between 0 and 1, -t2 is between -1 and 0. Let x = -t2. By our theorem with n = 4, for each x between -1 and 0 we have
Since c < 0 , 0 < ec < 1, and since x < 0 we have that `0 > R_4(x) > {x^5}/120`.
Substituting -t2 for x ,we see that
` e^{-t^2} = 1 + (-t^2) + {(-t^2)^2}/2 + {(-t^2)^3}/6 + {(-t^2)^4}/24 + R_4(-t^2)`
`= 1 + (-t^2) + {t^4}/2 - {t^6}/6 + {t^8}/24 + R_4(-t^2)`
Now since `0 > R_4(-t^2) > {(-t^2)^5}/120 = {-t^10}/120` we have `int_0^1 P_4(-t^2) dt > int_0^1 e^{-t^2} dt > int_0^1 P_4(-t^2) - {t^10}/120 dt`.
By evaluating these integrals we obtain
`1 - 1/3 +1/10 - 1/42 + 1/216 > int _0^1 e^{-t^2} dt > 1 -1/3 + 1/10 - 1/42 + 1/216 - 1/1320` .
Therefore,
and this is an overestimate by no more than `1/1320`.
Comment: We have been able to estimate
a definite integral involving the exponential function by using a Taylor
polynomial of degree 4. It should be apparent that by using a higher degree
for the estimating polynomial, the error term will become smaller and we
will obtain a more precise estimate. The systematic pattern in these polynomials
should allow you to find more precise estimates for `int_0^1 e^{-x^2} dx` without
much difficulty.
Proof of Proposition: We'll begin our proof by finding Pn'(x).
`P_n'(x) = 1 + x + {x^2}/2 + {x^3}/{2*3} + {x^4}/{4!} + ... +{nx^{n-1}}/{n!} `
`= 1 + x + {x^2}/2 + {x^3}/{2*3} + {x^4}/{4!} + ... + {x^{n-1}}/{(n-1)!} = P_{n-1}(x)`
From this it follows easily that ` P_n(0) = P_n '(0) = P_n''(0) =...= P_n^{(n)}(0) = 1`.
Now suppose that b is not 0 and let Rn = eb
-
Pn(b).
We need only justify the formula for evaluating Rn.
For convenience we'll write R = Rn and let
Furthermore `g'(t) = e^t*P_n(b-t) - e^t*P_n'(b-t)
- R* {(n+1)(b-t)^n}/{b^{n+1}}`
`= e^t* [P_n(b-t) - P_n'(b-t)] - R*{(n+1)(b-t)^n}/{b^{n
+ 1}}`
But `P_n(x) - P_n'(x) = {x^n}/{n!}, so
`g'(t) = e^t*{(b-t)^n}/{n!} - R* {(n+1)(b-t)^n}/{b^{n+1}}`.
Now we apply the Mean Value (or Rolle's) Theorem to the function g,
we can say that there is a number c between 0 and b where g'(c)=0.
Thus
`0 = g'(c) = e^c*{(b-t)^n}/{n!} - R* {(n+1)(b-t)^n}/{b^{n+1}}`
and
`e^t*{(b-t)^n}/{n!} = R* {(n+1)(b-t)^n}/{b^{n+1}}`.
Solving this last equation for R gives `R_n = R = e^c {b^{n+1}}/{(n+1)!}.