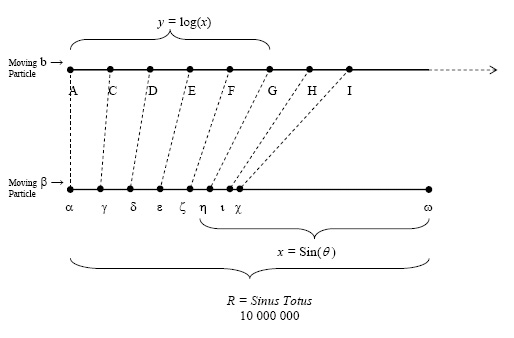
See:
http://www.maa.org/press/periodicals/convergence/logarithms-the-early-history-of-a-familiar-function-john-napier-introduces-logarithms
Logarithms: The Early History of a Familiar Function - John Napier Introduces Logarithms by Kathleen M. Clark (The Florida State University) and Clemency Montelle (University of Canterbury) ¤
Logarithms: The Early History of a Familiar Function - John Napier Introduces Logarithms by Kathleen M. Clark (The Florida State University) and Clemency Montelle (University of Canterbury) ¤