- If we have any two regions on the board of equal area then the dart would land in those regions about the same number of times with a large number of throws.
(a) If the board is divided into two regions by a concentric circle of radius 30 and I repeat the experiment a large number of times, what proportion of markings from the experiment is likely to lie in the inner region? See Figure 1.
(b) If the board is divided into four regions by concentric circles of radius 15, 30, and 45 cm and I repeat the experiment a large number of times, what proportion of the markings from the experiments is likely to lie in each of the regions?
(c) What proportion of the markings from repeating the experiment is likely for the dart to fall within A cms of the center
where 0<A<60? See Figure 2.
(d) If the board is divided into n regions by concentric circles of radius k * 60/n cms with k = 1,2 ... n-1, and I repeat the experiment a large number of times, what proportion of the markings from the experiments is likely in each of the regions?
2. Darts and Averages. Consider the same circular magnetic dart board with radius 60 centimeters. Draw 5 concentric circles on the board with radii 10,20,30,40, and 50 creating 6 regions (one disc and five bands). Consider the following game: Throw the dart at the board and score 5 points for landing in the inner disc, 15 points for landing in the smallest band (between the circles of radius 10 and 20), 25 points for landing in the next smallest band (between the circles of radius 20 and 30), 35 points for landing in the band between the circles of radius 30 and 40, 45 points for landing in the band between the circles of radius 40 and 50, and 55 points for landing in the outermost band (between the circle of radius 50 and the edge of the dart board). [In this game a low score is considered evidence of greater skill.]
We allow a player to throw a dart 36 times and find the total
score for the player as well as the average score (the total
divided by 36).
Notice the average will be a number between 5 and 55.
Give a total score and an average that are likely for a player
with no special skill. Discuss your reasoning and show the work
leading to your proposed solution.
[These numbers are described as
the expected score and the expected average for the game.]
Suggestion: You might investigate the similar problem with 2 regions and 4 throws and then 4 regions and 16 throws as a way to begin thinking about the problem. How many darts do you think would fall in each region?
Extension: (Optional) If we measure the distance each of the 36 darts fall from the center, what do you think the average distance would be for a player with no special skills. Explain your reasoning, any connections with the expected average score in the game, and whether you have any belief about the accuracy of your response. (Is it an underestimate or an overestimate?)
For example, the context of a marsh land environment is familiar to many residents of Arcata. Suppose that water is flowing from a stream into a marsh for 5 hours at 30000 cubic feet per hour. What change might be expected in the amount of water in the marsh and in the height of the water along an embankment at the end of the five hours. It should seem reasonable to you that after five hours the marsh will contain an additional 150000 cubic feet of water. We need more information about the shape of the marsh to determine the change in the height along the embankment. In particular we would need more information about the surface area of the marsh and the grade (steepness) of the embankment. We would also want to know how fast the water is flowing out of the marsh.
Describe a context in a similar fashion related to the following three settings. Indicate some of the important variables and rates that would be of interest for this context. Discuss how knowing these rates can be used to determine other information related to the original variables.
1. Automobile and truck traffic on Highway 101 or at a
major traffic intersection.
2. A flu epidemic in a population of school children.
(Consider Susceptible, Infected, and Recovered members of the
population.)
3. A college class room. (You might consider such
variables as number of people present, temperature, or level of
sound.)
Extension or Substitute for one of the above: Describe a
context related to a setting connected to your major or
some personal interest.
A. Suppose f(x) = x 3 + Bx
2 +2x + A. 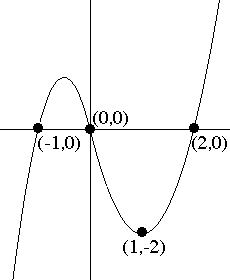
Find A and B so that f(0) = 1 and f '(1) = 7.
B.Let P(t) = K + Lt + Mt2 .
Find the coefficients K, L, and M so that P'(t) + P(t)
= t 2 + t + 1 for all t.
Hint: Consider the equation when t = 0, t = 1 and t = -1.
Making Curves Fit together Smoothly.
One way to make a curve that passes through several points and
looks smooth is to draw several curves that are defined by a
small number of points and make sure that when the curves are
joined together they have the same tangent lines, making the
connections appear smooth.
C. Use curves defined by two quadratic poynomial functions
to make a single smooth curve that passes through the four
points, (-1,0), (0,0), (1,-2) and (2,0) as in the figure.
Discuss briefly the strategy you used to find your solution.
Suggestion: Let P(x) = Ax2 + Bx+
C and Q(x) = Dx2 + Ex+ F.
Have the pair of curves meet at (0,0).
D. Find a second pair of quadratic polynomials which can be
used to make a single smooth curve that passes through the
same four points. [Hint: Have the pair of curves meet at
(1,-2).]
E. Find a single cubic polynomial that passes through the same
four points. [Hint: What are the linear factors of such a
polynomial?]
A.Follow up from POW #3. Find a cubic and a quadratic polynomial that can be used to make a single smooth curve that passes through the five points (-2,0), (-1,0), (0,0), (1,-2) and (2,0).
B. Fly-by-night Airlines has just announced a special summer charter flight fare for H.S.U. students from Arcata to Hawaii and return. A minimum of 80 students must sign up for each flight at a round trip fare of $210.00 per person. However, the airline has offered to reduce each student's fare by $1.00 for each additional student who joins the flight. Under these arrangements, what number of passengers will provide the airline with the greatest revenue per flight? Use calculus to justify your result.What kind of assumptions have you made about the functions you used in solving this problem?
C. Suppose you are given four constants
A, B, C, and D.
Let g(x) = (x - A)2 + (x - B)2+
(x - C)2 + (x - D)2. Using
calculus, for what value(s) of x does g(x) assume a minimum
value? Justify your answer briefly.
Generalize your result (if possible) for
1000 constants.
Assume P(x) is a solution to the differential equation P'(x) = 1/(1+x 2) with P(0) = 0.
B. Estimate P(1) using Euler's method with n = 10.
C. Let Q(x) = P(tan(x)). Use the chain rule and trigonometry to show that
Q'(x) = 1 for all x where -pi /2 < x < pi /2 .
D.Use C to explain why Q(x) = x for -pi /2 < x < pi /2 .[ Why is Q(0)= 0?]
E. Explain why P(1) = Q(pi/4) = pi /4.
A. Prove: If a = tan(a), then the line tangent to the graph of y=sin(x) at the point (a,sin(a)) passes through the origin. [Warning:Do not assume a=0.]
B. Prove: If the line tangent to the graph of y = sin (x) at the point (a, sin(a)) passes through the origin, then a = tan(a).
i. Draw a picture that illustrates the situation as described so far labelling points on the picture with the appropriate function values.
ii. Write an equation that expresses the statement that George always travels at the speed limit. [NOTE: The answer is not G'(t)= L(t).]
iii. Suppose that George always travels at the speed limit and that Martha's position at time t is George's position at time (t+5). Use the chain rule to show that Martha is always going at the speed limit.