Math 105 Spring, 2006

Assignments-SUBJECT TO REVISION!
#7: 4-18 to 4-25 #6: 4-4 to 4-13
 #5: 3-21 to 3-30
 #4: 3-2 to 3-9 #3:2-16 to 2-28
 #2: 2-7 to 2-16
 #1:1-24 to 2-7 #Final: Submit by ***
Resource List
Assignment #7: April 18 - April 25
Read Devlin: pp. 79-91 (Functions-slopes- the differential calculus)
                       pp.  94-97 (Finding areas and integral calculus).
           Stein    pp. 440-458 (More about infinity)
Exercises/Activities: No Special assignment for this week- time to work on projects and Portfolio entries:
Last minute suggestions:  Look at Stein problems related to chapters 5,6,7,14,15,17,and 19.
Usually there are 3-5 problems that fit together nicely to make an interesting portfolio entry.

Assignment #6: April 4 - April 13
Read Devlin: pp. 138-141 (Dimension)
                        pp. 74- 79 (The Infinite)
Exercises/Activities: To be collected on Thursday, April 13.

Higher dimensions.
I. The fourth dimension can be used to visualize and keep track of many things involvimg four distinct qualities that can be measured in some fashion.
A. For example, a 13 card bridge hand can be thought of as a point in four dimensions where the coordinates represent the number of cards of each suit present in the hand. In this context the point with coordinates ( 2, 4, 6, 1) might represent a hand with 2 clubs, 4 diamonds, 6 hearts and 1 spade.
Using this convention discuss briefly the following representations of bridge hands: (0, 0, 0, 13),  (0, 0, 6, 7),  (3, 3, 3, 4).
Suppose a bridge hand is represented by the point with coordinates (x, y, z, w).
Explain why x + y + z + w = 13.
B. Describe another context where four dimensions can be used in representing some features of the context.

II. Hypercubes in Higher Dimensions.
The 16 vertices of the 4-dimensional hypercube can be described by the collection of ordered quadruples (a,b,c,d) where the numbers  a, b, c, and d are either 0 or 1.
Write a description of the vertices of the 5-dimensional hypercube. How many vertices does the 5-dimensional hypercube have? How many vertices does the 6-dimensional hypercube have?  How many vertices does the 10-dimensional hypercube have? What can you say about the number of  vertices for the hypercube of dimension N?

III. The 4 - Simplex.
The edges of a tetrahedron in 3-dimensions can be drawn using 4 non-coplanar points on a cube. Draw the edges of the 4-dimensional analog of a tetrahedron, called a 4-simplex, by choosing 5 points (not all in the same 3-space) on the hypercube. (See Devlin, p. 140.)
The 4-simplex is made up of vertices, edges, triangles, and tetrahedra. Determine the number of edges and triangular faces in a 4-simplex.

The Infinite:
IV. Look up "Zeno's paradoxes" in the Encyclopedia (Britannica). Draw a figure that illustrates the paradox of Achilles and the Tortoise. Describe a common situation today to which Zeno's argument about Achilles and the Tortoise could be applied. Using your situation, discuss where the accumulation of small and infinitely divisible intervals is incorrectly compared with the accumulation of equally sized intervals.


Assignment #5: March 21-March 30
Read Devlin:    pp. 179-182.(The Moebius strip, orientability)
                          pp. 182-186, 187(1st paragraph.) (Surfaces)

Exercises/Activities: To be collected on Thursday, March 30.

I.Surfaces.
A. Describe 5 physical objects that have surfaces that are topologically equivalent to a (one hole) torus. Bring one example to class on Thursday.
B. Describe 2 physical objects that have surfaces that are topologically equivalent to a torus with two or more holes. Bring one example to class on Thursday.

II. Coloring the Torus and the Moebius Strip.
A. Draw a map on the Torus with 5 regions, each having a border with the other 4.
B. Draw a map on the Moebius Strip with 5 regions, each having a border with the other 4.

III. Models. Use paper or cloth to make a model of the Torus and the Klein Bottle.
Write instructions on how to put together these models. Discuss how these models relate to the following squares that are used to visualize these surfaces (in about one page) and how they might be assembled by "gluing" sides with the same label in the directions indicated by the arrows.
                 B                                             B           
   ┌──────────┐               ┌──────────┐       
   │             >           │               │            >            │       
   │^                      ^ │               │  ^                   ^  │       
A │                          │A          A│                          │A      
   │               >         │               │             <           │       
   └──────────┘               └──────────┘       
                   B                                           B           
            The Torus                          The Klein Bottle              

Assignment #4: March 2-March 9
Read Devlin:    pp. 174 - 175; 176 - 178 (Topology, Networks, and Euler's formula)
                        pp. 188-189 (The Four Color Problem)
        Stein:        Chapter 15 Map coloring

Exercises/Activities: To be collected on Thursday, March 9

I.Group the following letters, as printed on this page, together in different classes determined by whether they are topologically equivalent. [It is up to you to determine the appropriate classes.]
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
  
II. Networks and Euler's Formula.
A. A message has arrived from the planet Yxo describing a road network connecting 8 major cities on the planet. The message claims that the network has exactly 15 edges and divides the planet into 6 separate regions. Based on Euler's formula discuss the following statement:
Either the planet is not spherical in general shape or the information is incomplete.
B. A planar graph has been drawn by a designer using exactly 12 edges and 8 vertices. How many regions are created by this graph?   Explain how you arrived at your count.
Draw a graph that is evidence that such a graph is possible.

III. Networks As Models.
Choose a floor in a building on the Occidental campus.
A. Describe the layout of this floor as a network. Include a sketch of the network together with a legend explaining the correspondence of vertices and edges to the building's features.
B. Suppose there is an electrical blackout at night. Discuss how you could use your network description to help find your way through the floor to leave the building.
C. Compare the situation of the floor layout network to Devlin's London Underground Network. How are their uses alike? How do they differ?

III. Maps.
Find three different types of world maps. Copy each by tracing or photo or by “cut and paste”. Write a short report (about one page) describing how both the poles and the global coordinates determined by longitude and latitude are visualized on each planar map.
Assignment #3: February 16 -February 28
Read Devlin:    pp. 112-115;
Read Devlin:  p. 115-119;pp. 112-115 (Euclid- inscribed angles in semicircles,Platonic solids, Plato, and Kepler)
pp 129-132 (Introduction to the geometry of projection)
Plato's Cave Metaphor- online.

 I.Creating new tessellations by modifications.
Create a tessellation of curved figures following the ideas from the activity of February 14th applied to the regular tiling of the plane by (1) hexagons and (2) equilateral triangles.

II. The Sphere has brought the Cube to visit his new friend in Flatland. Describe two possible successions of different planar shapes the Cube might  appear as while passing through Flatland.
Draw the sequences as they would be seen in Flatland.        

III. Projections: Casting Shadows on Flatland.
The sphere is still trying to explain some of the features of the torus to a Flatlander. This time the sphere has decided to show the Flatlander different shadows that are cast by the projection of the torus onto Flatland.
A. Draw three different shadows that the torus could cast.
B. Do you think it is possible to make a torus that would cast a shadow on Flatland that completely covers a circle and its interior? If so, describe some of the features of such a torus. If not, give some reasons for your belief. In other words, is it possible that a Flatlander might mistake a torus for a sphere based on the shadow it casts?

IV.Lineland Paper:
    Imagine you are a Flatlander talking to a Linelander. Write an explanation of symmetry to a Linelander from the point of view of a Flatlander. Discuss and illustrate the kinds of symmetry that are possible in Lineland. Which Flatland symmetries (if any) would you associate with Lineland symmetries? Explain the association briefly.
Here are some terms you might use in your discussion: Reflection  Rotation  Translation  Orientation

V.Plato and Shadows: The Greek philosopher Plato describes a situation where a person lives in a cave and can only perceive what happens outside the cave by observing the shadows that are cast on the walls of the cave from the outside.

Write a brief essay discussing a situation in the contemporary world where indirect experiences are used to make observations. How are the observations made? How are they connected to the actual situation? Do you think the inferences made from the observations are always accurate? [3 or 4 paragraphs should be adequate.]


Assignment #2: February 7 - February 16
Read Flatland:    Part II.
Read Devlin:    pp. 144-150 (Symmetry Groups); pp. 165-169 (Tiling).
Read Stein: pp. 218-227
Exercises/Activities: To be collected on Thursday February 16.

I. Classifications by reflection and rotation symmetries:
   It is often useful to classify visual objects by their symmetries. For example, the letter "T" as it appears on this page has only a reflection symmetry determined by a vertical line, whereas the letter "I" has two reflection symmetries and a 180 degree rotational symmetry and "J" has no symmetries.

Group the following letters, as printed on this page, together in different classes determined by the reflection and rotational symmetries they have. [It is up to you to determine the appropriate classes.]
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

II. Assume the following pattern is extended indefinitely on the plane. This pattern has many lines of reflectional symmetry.  Draw in all the lines of symmetry using colored pencils so that any two lines with the same color are parallel and any two lines that are parallel are colored with the same color.


III. Find (or create) a graphic design (in advertisements, logos, or icons) that
(i) has exactly one reflection symmetry, (ii) has exactly two reflection symmetries, and (iii) has exactly three reflection symmetries.
 Indicate and discuss the symmetry line(s) in each separate design.

IV. [This problem may be done with a partner]. Symmetry group of a square.
    There are 8 symmetries for any square.
    A. Provide a sketch of the square and illustrate the 8 symmetries as in the triangle example. [See the class notes.]
    B. Determine the "multiplication table" for the group of symmetries of the square. [See Devlin page 150] 
.
Assignment #1: January 24 - February 7.(revised 1-30)
Read Flatland. Introduction, Preface, and Part I.
(Activity and assignments on Flatland will follow next week.)
Read Devlin:    Prologue, pp. 1-7. 
            Chapter 1, Greek Mathematics, pp. 14 - 18, 21, and 31.
Added (1-31) Stein :  Preface.  Chapter 4 pp 56-62.

Exercises/Activities: To be collected on Tuesday, February 7. (revised 1-30)

I. Ask your adviser or an instructor you know in your major the following two questions:
    A. How do you define mathematics?  (or What is mathematics?)
    B. Can you give one example of how mathematics is used in your discipline? Ask for an explanation of the response.

Report the responses to these two questions and relate them to Devlin's treatment of question A.
[Two paragraphs are sufficient.]
 
II. Using the seven pieces of the tangram puzzle create
A. A rectangle   and B. A right triangle.

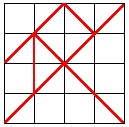
II. Suppose that the square made using the seven tangram pieces as shown above has a side of length 4.

A. Find the length of the sides of each of the seven pieces.
B. Find the area of each of the seven pieces.  

III. [See Devlin, p.21]
Draw a rectangular figure arranging 30 discs into 5 rows.
    A. Draw a straight line through the rectangle that divides the discs into two triangular groups each with 15 discs.
    B. According to the formula on Devlin page 21, using n = 5, 
  1 + 2 + 3 + 4 + 5 = 5 (5+1) / 2.
Explain the relation of this equation to the arrangement of the 30 balls in part A.
    C. Describe an analogous figure to explain why
    1 + 2 + 3 + ⋯ + 98 + 99 + 100 = 10,100/2 = 5,050
________________________________

Other resources (portfolio/projects) for assignment #1:
Over 30 proofs of the Pythagorean theorem!
Many Java Applets that visualize proofs of the Pythagorean Theorem
TANGRAMS -- history -- puzzles -- make -- links

Japanese Site
Printout Tangram puzzles

and play anytime anywhere
Web references related to scissors congruence - dissections. 
Final Course Assignment .
[May be submitted until ***]
Over the term we have covered many topics in class and through the readings. Choose two topics we have studied for examples in writing a paper (1-3 pages) discussing one of the following statements:
     A. The study of visual mathematics in two dimensions has much in common but also some noticable differences with its study in three dimensions.
     B. The amazing thing about mathematics is how it is able to turn even the simplest things into abstractions and can make the subtlest of concepts clear through a figure.
 

Resource List for Portfolio Entries

The following list contains suggestions  for finding resources as well as the names of resources that may be used for one or more portfolio entries. Before reading an article in one of these resources thoroughly it is advisable to scan it quickly to see that it contains something of interest to yourself. Your portfolio entry can report on the content of your reading, illustrate it by examples, and/or follow up on it with your own response and creativity.

The content of the portfolio entry should relate specifically and directly to some visual mathematics. Personal observations , philosophical musings, and aesthetical judgments are not adequate connections to something visual by themselves to qualify as mathematical content.

These articles may also be useful in developing a deper level of understanding on a topic which will suppport your term project. I will add to this list as the term progresses.