Math 105 Spring, 2006
Resource List
Assignment #7:
April 18 - April 25
Read Devlin: pp. 79-91
(Functions-slopes- the differential calculus)
pp. 94-97 (Finding areas and integral calculus).
Stein
pp. 440-458 (More about infinity)
Exercises/Activities: No Special assignment for this week-
time to work on projects and Portfolio entries:
Last minute suggestions: Look at Stein problems related to
chapters 5,6,7,14,15,17,and 19.
Usually there are 3-5 problems that fit together nicely to make an
interesting portfolio entry.
Assignment #6:
April 4 - April 13
Read Devlin: pp. 138-141 (Dimension)
pp. 74- 79 (The Infinite)
Exercises/Activities: To be collected on
Thursday, April 13.
Higher dimensions.
I. The fourth dimension can be used to
visualize and keep track of many things involvimg four distinct
qualities that can be measured in some fashion.
A. For example, a 13 card bridge hand
can be thought of as a point in four dimensions where the coordinates
represent the number of cards of each suit present in the hand. In this
context the point with coordinates ( 2, 4, 6, 1) might represent a hand
with 2 clubs, 4 diamonds, 6 hearts and 1 spade.
Using this convention discuss briefly
the following representations of bridge hands: (0, 0, 0, 13), (0,
0, 6, 7), (3, 3, 3, 4).
Suppose a bridge hand is represented
by the point with coordinates (x, y, z, w).
Explain why x + y + z + w = 13.
B. Describe another context where four
dimensions can be used in representing some features of the context.
II. Hypercubes in Higher Dimensions.
The 16 vertices of the 4-dimensional
hypercube can be described by the collection of ordered quadruples
(a,b,c,d) where the numbers a, b, c, and d are either 0 or 1.
Write a description of the vertices of
the 5-dimensional hypercube. How many vertices does the 5-dimensional
hypercube have? How many vertices does the 6-dimensional hypercube
have? How many vertices does the 10-dimensional hypercube have?
What can you say about the number of vertices for the hypercube
of dimension N?
III. The 4 - Simplex.
The edges of a tetrahedron in 3-dimensions can be drawn using 4
non-coplanar points on a cube. Draw the edges of the 4-dimensional
analog of a tetrahedron, called a 4-simplex, by choosing 5 points (not
all in the same 3-space) on the hypercube. (See Devlin, p. 140.)
The 4-simplex is made up of vertices, edges, triangles, and tetrahedra.
Determine the number of edges and triangular faces in a 4-simplex.
The Infinite:
IV. Look up "Zeno's paradoxes" in the Encyclopedia (Britannica). Draw a
figure that illustrates the paradox of Achilles and the Tortoise.
Describe a common situation today to which Zeno's argument about
Achilles and the Tortoise could be applied. Using your situation,
discuss where the accumulation of small and infinitely divisible
intervals is incorrectly compared with the accumulation of equally
sized intervals.
Assignment #5:
March 21-March 30
Read Devlin: pp.
179-182.(The Moebius strip, orientability)
pp.
182-186, 187(1st paragraph.) (Surfaces)
Exercises/Activities: To be collected on Thursday, March
30.
I.Surfaces.
A. Describe 5 physical objects that have surfaces that are
topologically equivalent to a (one hole) torus. Bring one example to
class on Thursday.
B. Describe 2 physical objects that have surfaces that are
topologically equivalent to a torus with two or more holes. Bring one
example to class on
Thursday.
II. Coloring the Torus and the Moebius Strip.
A. Draw a map on the Torus with 5 regions, each having a border with
the
other 4.
B. Draw a map on the Moebius Strip with 5 regions, each having a border
with the other 4.
III. Models. Use paper or cloth
to make a model of the Torus and the Klein Bottle.
Write instructions on how to put together these models. Discuss how
these models relate to the following squares that are used to visualize
these surfaces (in about one page) and how they might be assembled by
"gluing" sides with the same label in the directions indicated by the
arrows.
B
B
┌──────────┐
┌──────────┐
│
>
│
│ >
│
│^
^
│
│ ^
^
│
A │
│A
A│
│A
│
>
│
│
<
│
└──────────┘
└──────────┘
B
B
The
Torus
The Klein
Bottle
Assignment #4:
March 2-March 9
Read Devlin: pp. 174 - 175; 176 -
178
(Topology, Networks, and Euler's formula)
pp. 188-189
(The Four Color Problem)
Stein:
Chapter 15 Map coloring
Exercises/Activities: To be collected on Thursday, March 9
I.Group the following letters, as printed on this page,
together in different classes determined by whether they are
topologically equivalent. [It is up to you to determine the appropriate
classes.]
A B C D E F G H I J K
L M N O P Q R S T U V W X Y Z
II. Networks and Euler's Formula.
A. A message has arrived from the planet Yxo describing a road network
connecting 8 major cities on the planet. The message claims that the
network
has exactly 15 edges and divides the planet into 6 separate regions. Based
on Euler's formula discuss the following statement:
Either the planet is not spherical in general shape or the
information is incomplete.
B. A planar graph has been drawn by a designer using exactly 12 edges
and 8 vertices. How many regions are created by this graph?
Explain how you arrived at your count.
Draw a graph that is evidence that such a graph is possible.
III. Networks As Models.
Choose a floor in a building on the Occidental campus.
A. Describe the layout of this floor as a network. Include a sketch of
the network together with a legend explaining the correspondence of
vertices
and edges to the building's features.
B. Suppose there is an electrical blackout at night. Discuss how you
could use your network description to help find your way through the
floor to
leave the building.
C. Compare the situation of the floor layout network to Devlin's London
Underground Network. How are their uses alike? How do they differ?
III. Maps.
Find three different types of world maps. Copy each by tracing or photo
or by “cut and paste”. Write a short report (about one page) describing
how both the poles and the global coordinates determined by longitude
and latitude are visualized on each planar map.
Assignment
#3: February 16 -February 28
Read
Devlin: pp. 112-115;
Read
Devlin:
p.
115-119;pp. 112-115 (Euclid- inscribed
angles in semicircles,Platonic
solids, Plato, and Kepler)
pp 129-132 (Introduction to the geometry of projection)
Plato's Cave Metaphor-
online.
I.Creating new
tessellations by modifications.
Create a tessellation of curved figures following the ideas from the
activity of February 14th applied to the regular tiling of the plane
by (1) hexagons and (2) equilateral triangles.
II. The Sphere has brought the Cube to visit
his new friend in Flatland. Describe two possible successions of
different planar shapes the Cube might appear as while passing
through Flatland.
Draw the sequences as they would be seen in
Flatland.
III. Projections: Casting Shadows on Flatland.
The sphere is still trying to explain some of the features of the torus
to a Flatlander. This time the sphere has decided to show the
Flatlander
different shadows that are cast by the projection of the torus onto
Flatland.
A. Draw three different shadows that the torus could cast.
B. Do you think it is possible to make a torus that would cast a shadow
on Flatland that completely covers a circle and its interior? If so,
describe some of the features of such a torus. If not, give some
reasons for your belief. In other words, is it possible that a
Flatlander might mistake a torus
for a sphere based on the shadow it casts?
IV.Lineland Paper:
Imagine you are a Flatlander talking to a
Linelander. Write an explanation of symmetry to a Linelander from the
point of view of a Flatlander. Discuss and illustrate the kinds of
symmetry that are possible in Lineland. Which Flatland symmetries (if
any) would you associate with Lineland symmetries? Explain the
association briefly.
Here are some terms you might use in your discussion: Reflection
Rotation Translation Orientation
V.Plato and Shadows: The Greek philosopher Plato
describes a situation where a person lives in a cave and can only
perceive what happens outside the cave by observing the shadows that
are cast on the walls of the cave from the outside.
Write a brief essay
discussing a situation in
the contemporary world where indirect
experiences are used to make observations. How are the
observations
made? How are they connected to the actual situation? Do you think the
inferences made from the observations are always accurate? [3 or 4
paragraphs should be adequate.]
Assignment
#2: February 7 - February 16
Read
Flatland:
Part II.
Read Devlin: pp.
144-150 (Symmetry Groups); pp. 165-169 (Tiling).
Read Stein: pp. 218-227
Exercises/Activities: To be
collected
on Thursday February 16.
I. Classifications by reflection
and rotation
symmetries:
It is often useful to classify visual objects by their
symmetries. For example, the letter "T" as it
appears on this page has only a reflection symmetry determined by a
vertical line, whereas the letter "I" has two
reflection symmetries and a 180 degree rotational symmetry and "J"
has no symmetries.
Group the following letters, as printed on this page,
together in different classes determined by the reflection and
rotational
symmetries they have. [It is up to you to determine the appropriate
classes.]
A B C D E F G H I J K
L M N O P Q R S T U V W X Y Z
II. Assume the following pattern is extended indefinitely on the plane.
This pattern has many lines of reflectional symmetry. Draw in all
the lines of symmetry using colored pencils so that any two lines with
the same color are parallel and any two lines that are parallel are
colored with
the same color.
III. Find (or create) a graphic design (in advertisements, logos, or
icons) that
(i) has exactly one reflection symmetry, (ii)
has exactly two reflection symmetries, and (iii) has exactly three
reflection symmetries.
Indicate and discuss the symmetry line(s) in
each separate design.
IV. [This problem may be done with a partner]. Symmetry
group
of a square.
There are 8 symmetries for any square.
A. Provide a sketch of the square and illustrate the
8 symmetries as in the triangle example. [See the class notes.]
B. Determine the "multiplication table" for the
group of symmetries of the square. [See Devlin page 150]
.
Assignment
#1: January 24 - February 7.(revised 1-30)
Read Flatland. Introduction, Preface, and Part I.
(Activity and assignments on Flatland will follow next week.)
Read Devlin:
Prologue, pp. 1-7.
Chapter 1,
Greek Mathematics, pp. 14 - 18, 21, and 31.
Added (1-31) Stein : Preface. Chapter 4 pp 56-62.
Exercises/Activities: To be collected on Tuesday, February
7. (revised 1-30)
I. Ask your adviser or an
instructor you know in your major the following two questions:
A. How do you define mathematics? (or What
is mathematics?)
B. Can you give one example of how mathematics is
used in your discipline? Ask for an explanation of the response.
Report the responses to these two
questions and relate them to Devlin's treatment of question A.
[Two paragraphs are sufficient.]
II. Using the seven pieces of the tangram puzzle create
A. A rectangle and B.
A right triangle.
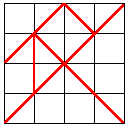
II. Suppose that the square made using the seven tangram pieces
as shown above has a side
of length 4.
A. Find the length of the sides of each of the seven pieces.
B. Find the area of each of the seven pieces.
III. [See Devlin, p.21]
Draw a rectangular figure arranging 30 discs into 5 rows.
A. Draw a straight line through the rectangle that
divides the discs into two triangular groups each with 15 discs.
B. According to the formula on Devlin page 21, using
n = 5,
1 + 2 + 3 + 4 + 5 = 5 (5+1) / 2.
Explain the relation of this equation to the arrangement of the 30
balls in part A.
C. Describe an analogous figure to explain why
1 + 2 + 3 + ⋯
+ 98 + 99 + 100 = 10,100/2 = 5,050
________________________________
Other resources (portfolio/projects) for
assignment #1:
Over 30
proofs of the
Pythagorean theorem!
Many Java
Applets that visualize proofs of the Pythagorean Theorem
TANGRAMS -- history --
puzzles -- make -- links
|

|
Japanese Site
Printout Tangram puzzles
and play anytime
anywhere
|
|
Web
references related to scissors congruence - dissections.
Final
Course Assignment .
[May be submitted until ***]
Over the term we have covered many topics in class and through the
readings. Choose two topics we have studied for examples in writing a
paper (1-3 pages) discussing one of the following statements:
A. The study of visual mathematics in two
dimensions has much in common but also some noticable differences with
its study in three dimensions.
B. The amazing thing about mathematics is how
it is able to turn even the simplest things into abstractions and can
make the subtlest of concepts clear through a figure.
Resource List for
Portfolio Entries
The following list contains suggestions for finding resources as
well as the names of resources that may be used for one or more
portfolio entries. Before reading an article in one of these resources
thoroughly it is advisable to scan it quickly to see that it contains
something of interest to yourself. Your portfolio entry can report on
the content of your reading, illustrate it by examples, and/or follow
up on it with your own response and creativity.
The content of the
portfolio entry
should relate specifically and directly to some visual mathematics.
Personal
observations , philosophical musings, and aesthetical judgments are not
adequate
connections to something visual by themselves to qualify as
mathematical
content.
These articles may also be useful in developing a deper level of
understanding on a topic which will suppport your term project. I will add to this list as the term progresses.
- The EASY way: Several chapters
from the course texts will not be
covered in class but can be used for portfolio entries. An entry based
on our text should report on a selection of the included exercises
along with the content of the chapter.
- More adventuresome: Use
my collection of Visual
Mathematics web sites for surfing visual mathematics and geometry.
- Use articles from old Scientific American magazines
(available
on-line?)
- (Older issues) Martin Gardiner's articles are usually short
and clear enough to provide material for one or even two even entries.
- (More recent issues) Ian Stewart 's articles are similar and
about as playful as the Gardner pieces.
- Some issues have had articles on special topics that
are relevant to our interests. These are usually longer and require a
little more effort to digest - though well worth the effort.
- "Topology" by Tucker and Bailey, 1950, pp 8-24.
- A number of liberal arts / mathematics textbooks contain
chapters that would be suitable for reporting.
- Mathematics: the Man-made
Universe by Sherman
Stein.
- Excursions into Mathematics by Beck, Bleicher, and
Crowe.
- What is Mathematics? by Courant and Robbins.
- The World of Mathematics by Newman.
- There are several non-text mathematics books and collections
of essays.
- Mathematics: The Science of
Patterns by K.
Devlin
- Beyond the Third Dimension by T. Banchoff.
- Martin Gardiner has many books full of puzzles and recreations
many of which are relevant.
- The Problems of Mathematics by Ian Stewart.
- The Mathematical Experience by Philip Davis and Reuben
Hersh




