- Course Description.
- What is synthetic geometry?
- What is analytic geometry?
- transformations
- geometry as an empirical science
- geometry as a formal system of information
- geometry focused on special objects like triangles, or special qualities like convexity.
- A figure C is called convex if given any two points in the figure, A and B, the line segment AB is a subset of the figure.
- Examples. An elliptical region in the plane is convex. A lunar region in the plane is not convex. [Here is an interesting piece of geometry related to the area of lunes.]
- Geometry on the web and using GSP and Wingeom 2D Introduction.
- The Pythagorean Theorem using GSP.
Other aspects of geometry briefly
.
- Geometry has traditionally been interested in both results- like the Pythagorean Theorem- and foundations - using axioms to justify the result in some rigorous organization. We will be concerned with both results and foundations.
- In the distinction between synthetic and analytic geometry the key connecting concept is the use of measurements. Initially we will try to avoid the use of measurement based concepts when possible.
- To explore some of these issues, let's looked at the proofs of the Pythagorean Theorem.
- First consider Euclid's statement and proof of Proposition 47.
Note that Euclid's treatment in its statement or its "proof" never refers
the traditional equation, a2+b2=c2.
In one alternative proof for this theorem illustrated in the java sketch
below, we consider 4 congruent right triangles and 2 squares and then the
same 4 triangles and the square on the side of the hypotenuse arranged
inside of a square with side "a+b" . Can you explain how this sketch
justifies the theorem?
- Another
proof using "shearing" illustrated in the Java sketch below taken from
a Geometers' Sketchpad example can be connected to Euclid's proof..
- Shear the squares on the legs by dragging point P, then point Q, to the line. Shearing does not affect a polygon's area.
- Shear the square on the hypotenuse by dragging point R to fill the right angle.
- The resulting shapes are congruent.
- Therefore, the sum of the squares on the sides equals the square on the hypotenuse.
(Based on Euclid's Proof) D. Bennett 10.9.9
- In considering the Pythagorean theorem, what kind of assumptions were
needed in the first proof with the triangles and squares?
- How could we justify identifying "equal" objects (congruent figures)?
- How do the objects fit together?
- How do movements effect the shapes of objects.
Here are some considerations related to those assumptions:
- Consider Euclid's Proposition 1 and Proposition 2.
- These propositions demonstrate that Euclid did not treat moving a line segment as an essential property worthy of being at the foundations as an axiom. However, this is a fundamental tool for all of geometry.
- Note that in the proofs of these propositions certain points of intersection of circles are presumed to exist without reference to any of the postulates. These presumptions were left implicit for hundreds of years, but were cleared up in the 19th century when careful attention was given again to the axioms as a whole system.
[An example of a geometry where circles do not intersect is given by using the rational coordinate plane. Points correspond to ordered pairs of rational numbers. then the circle with center (0,0) and radius 1 and the circle with center (1,0) also radius 1 meet in the ordinary plane at the points with coordinates (1/2, sqrt(3)/2) and (1/2, -sqrt(3)/2) . Since sqrt(3)/2 is not a rational number, this ordered pair does not correspond to a point in the rational coordinate plane, so the two circles do not have a point of intersection.
Another example of a point not in the rational coordinate plane is the point (sqrt(2),0). This point can be constructed in the ordinary plane with straight edge and compass using the circle with center (0,0) and radius determined by the points (0,0) and (1,1). This circle will meet the X-coordinate axis at the point (sqrt(2),0) ]
- 1. Construct a sketch with technology of Euclid's
Proposition 1 in Book I.
2. Construct a sketch with technology of Euclid's Proposition 2 in Book I.
3. Construct a sketch with technology of one "proof" of the Pythagorean Theorem.
1. Dissections: How are figures cut and pasted together? What can be achieved using dissections?
2. Transformations: How are figures transformed? What transformations will leave the "area" and "lengths" of figures invariant (unchanged)?
In the Next Section: We'll look at the possibilities of dissections .
- Use tangram pieces to make a square.
- Note that in putting the pieces together to form any other shape, the area of that shape would be the same as the area of the square unless there is some overlap of the pieces in the shape.
Comment: In a sense a positive (yes) response to this question means
that one could create a set of smaller shapes with which one could make
either of the two regions using precisely these smaller shapes. The answer
to this question is yes (in fact this is a 20th century result), which
is the basis for the remainder of this section
[The analogous problem in three dimensional geometry: volume equality
of polyhedra is a necessary but not sufficient condition for a similar
result. This was the third of the famous
23 "Hilbert problems" for the 20th century. This was first demonstrated
by Dehn in the 1930's by using another invariant of polyhedra related to
the lengths of the edges and the dihedral angles between the faces of the
polyhedra. References to be supplied]
First, consider some of the background results which were known to Euclid: (1) parallelograms results and (2) triangle results. The justifications for these results can be reviewed briefly.
(1) a. Parallelograms between a pair of parallel lines and on the same
line segment are equal (in the sense of being able to decompose one to
reconstruct the other). Proposition
35.
b. Parallelograms between a pair of parallel lines and on congruent
segments are equal (in the sense of being able to decompose one to reconstruct
the other). Proposition
36.
(2) a. The line segment connecting the midpoints of two sides
of a triangle is parallel to the third side and is congruent to one half
of the third side.
[The justification of this result was discussed,
but no proof was given. This is a question that will be considered in the
next meeting on Tuesday.]
b. By rotating the small triangle created by connecting the midpoints
of two sides of a triangle 180 degrees about one of the midpoints, we obtain
a parallelogram. (This shows that the triangle's area is the area
of this parallelogram which can be computed by using the length of the
base of the triangle and 1/2 of its altitude- which is the altitude of
the parallelogram.)
2/6 (i) Justification of the result (2)a on midpoints
of the sides of a triangle;
This proposition had not been proven by anyone in class... so
it was added to the problems to be done for the next class. [Either create
a proof or find one... possibly in Euclid.]
(ii) The triangulation of any polygonal region
in the plane was used in the proof of the equidecomposable
polygon theorem.
The proof of this proposition examines a more careful characterization
of the polygonal regions being considered. The key idea of the proof goes
by induction on the number n = the number vertices = the number of sides
in the polygon, as follows:
When n = 3 the result is trivial.
Suppose n> 3 and that for any polygon with k vertices/ sides, where
k<n, the polygon can be triangulated.
Now proceed to consider the vertices, v1, v2, ..., vn ordered
so that vi is adjacent to vi+1 and vn is adjacent to v1.
Take a ray from v1 and rotate it from v1v2 so that it intersects
the inside of the polygon. continue to rotate until it meets another vertex.
Case 1. This vertex is v3. Then consider the polygonal region Q1
= v1v3...vn which has n-1 vertices. By induction Q1 can be triangulated,
so the original polygon is triangulated using the triangulation of Q1 and
the triangle v1v2v3.
Case 2. The vertex is vn. Then consider the polygonal region Q2
= v2v3...vn which has n-1 vertices. By induction Q2 can be triangulated,
so the original polygon is triangulated using the triangulation of Q2 and
the triangle v1v2vn.
Case 3. The vertex is vk with k different from 3 or n. Then consider
the polygonal regions Q3 = v1v2...vk which has k vertices (k<n) and
Q4 = v1vkvk+1...vn which has n-(k-2)<n vertices. By induction Q3 and
Q4 can be triangulated, so the original polygon is triangulated using the
triangulations of Q3 and Q4.
For more discussion of proofs of this proposition see Triangulations
and arrangements, Two lectures by Godfried Toussaint, transcribed by
Laura Anderson and Peter Yamamoto.
The lecture also included a discussion briefly of how to "add parallelograms", which is used for the same proof of the equidecomposable polygon theorem.
The film Equidecomposable Polygons also proves the result:
If two polygonal regions in the plane have the same area, then there
is a decomposition of each into polygons so that these smaller polygons
can be moved individually between the two polygons by translations or half
turns (rotations by 180 degrees).
Laboratory Exercises: Due
by Friday, Feb. 9.
1. Show how to "add" two arbitrary triangles
to create a single parallelogram. <---This is now optional.
2. Do Construction 3, 4, 6, 7, and 8 from
Meserve and Izzo Section 1.2.
REVIEW of basic plane geometry concepts and definitions.
M&I build their foundations for Euclidean geometry on a one to one correspondence between points on a line and real numbers and the ability to match angles with numbers between 0 and 180.
After reviewing materials defining, rays, segments, angles, triangles,
and planes,
review eight of the basic Euclidean constructions
described in M&I
section 1.2. Note that several of these constructions
rely on some foundations that assert the existence of points of intersection
of circles.
2/8: The
midpoint proposition.
Some comments about Constructions: It is important
to notice that constructions also require a justification (proof) that
the construction has in fact been achieved. In proving the constructions
we use some basic euclidean results, such as the congruence of all corresponding
sides in two triangles is sufficient to imply the triangles are congruent
(SSS). [Other basic Euclidean results are SAS and ASA congruence conditions,
and well as the result that corresponding parts of congruent triangles
are congruent (CPCTC).]
In considering constructions of tangents to circles we use the characterization
of a tangent line as making a right angle with a radius drawn at the point
it has in common with the circle. ( Book
III Prop. 16.) In our construction, not Euclid's (Book
III Prop. 17), we also use the result that any angle inscribed in a
semi-circle is a right angle. ( Book
III Prop. 31.)
First construct Pk where k is an integer using circles.
We can construct points with fractions using powers of 2 for the denominator by bisection.
[At this stage review the construction of a line though a given point parallel to a given line. See Euclid I.31.]
We can also construct Pk when k is a rational number using the theory of similar triangles.
(With only bisection we could not construct a point for 1/3 although we could get very close to that point using a binary representation of that common fraction.)
Consider M&I's constructions of the same correspondence of integer and rational points. These also rely on the ability to construct parallel lines.
At this stage we should discuss the continuity axiom for a euclidean line:
- Any nonempty family of nested segments will have at least one point in the intersection of the family.
I.e., given P0 and P1 for any
real number x there is a point Px where a<x<b
if
and only if Px is between Pa
and Pb and the point Pk . corresponds
to the number k for any rational number k.
The continuity axiom leads to the important result due to G. Cantor that any list (possibly infinite) of points in a given segment of a euclidean line will not have every point in that segment on the list. [Note that we can make a list of points corresponding to the rational numbers once a unit length had been established. 1/1,1/2,2/1,1/3,2/2,3/1,1/4,2/3,3/2,4/1, ....]
The continuity axiom can also be used to prove: If a line, l, (or circle, O'A') has at least one point inside a given circle OA and one point outside the same given circle then there is of a point on the line (circle) that is also on the given circle.
Proof outline for the line-circle:Use bisection between the points on the line l outside and inside the circle OA to determine a sequence on nested segments with decreasing length approaching 0. The point common to all these segments can be shown to lie on the circle OA.
Proof outline for the circle-circle: Draw the chord between the inside and outside points on the circle O'A'. Use bisection on this chord to determine rays that by the previous result will meet the circle O'A'. The bisections can continue to determine a sequence of nested segments with decreasing length approaching 0 and with endpoints determining one outside point and one inside on O'A' . The point common to all the endpoints on the chord will determine a point on O'A' that can be shown to also lie on OA.
Note: The circle-circle result fills in a hole
in the proof of Proposition 1 in Book I of Euclid.
Recall the Definition: A figure F is convex if whenever A and B are points in F, the line segment AB is a subset of F.
The half plane example:Consider the half plane determined by a line l and a point P not on the line. This can be defined as the set of points Q in the plane where the line segment PQ does not meet the line l. Discuss informally why the half plane is convex.
Review the problems on convex figures in Problem Set 1.
Other convex examples: Apply the intersection property [The intersection
of convex sets is convex.] to show that the interior of a triangle is convex.
Show that the region in the plane where (x,y) has y>x2
is convex using the tangent lines to the parabola y=x2 and the
focus of the parabola to determine a family of half planes whose intersection
would be the described region.
Isometries:
Now consider Euclid's treatment of the side-angle-side congruence [Proposition
4] and how it relates to transformations of the plane that preserve
lengths and angles. Such a transformation T: plane -> plane, has T(P)=P',
T(Q)=Q' and T(R)=R' with d(P,Q) = d(P',Q') [distance between points are
preserved] or m(PQ)=m(P'Q') [measures of line segments are invariant].
Review briefly the outline of Euclid's argument for Proposition
4.
Notes:
- The Side-side-side (SSS) congruence of triangles (If Corresponding sides of two triangles are congruent, then the triangles are congruent), allows one to conclude that any isometry also transforms an angle to a congruent angle.
- The key connection between the congruence of figures in the plane and isometries: Figures F and G are congruent if and only if there is an isometry of the plane T so that T(F) = {P' in the plane where P'= T(P) for some P in F} = G.
You can read more about isometries by checking out this web
site:
Introduction
to Isometries.
Line Isometries: Consider briefly isometries of a
line.
1) translations and 2) reflections.
How can we visualize them?
Transformations figures (before and after lines); Correspondence figure
on a single line; Graph of transformation; Coordinate function?
Can we classify them? Is every line isometry either a translation or
a reflection?
There are at least four types of isometries of the plane: translation,
rotation, reflection and glide reflection.
Lab Exercises Due Friday Feb. 16.
1. Construct a scalene triangle using Wingeometry. Illustrate how to do
i) a translation by a given "vector", ii) a rotation by a given angle measure,
and iii) reflections across a given line..
2. Create a sketch that shows that the product
of two reflections is either a translation or a rotation.
2/15 The classification
of isometries.
Recall the informal definition of an isometry: A transformation (function)
that preserves "distance."
We can visualize a plane isometry using one plane; two planes or (perhaps) a graph. [A graph here would require four dimensions!]
For an isometry T where T(P) = P', when we know T(A), T(B), and T(C) for A,B, and C three noncolinear point , then T(P) is completely determined by the positions of A', B', and C'. In fact we saw that T(B)=B' must be on the circle with center A' and radius= m(AB), and T(C)= C' must be on the intersection of the circles one with center at A' and radius = m(AC) and the other with center at B' and radius=m(BC). Once these points are determined, then for any point P, P' must be on the intersection of 3 circles, centered at A', B', and C' with radii = to m(AP), m(BP), and m(CP) respectively. These three circles do in fact share a single common point because the associated circles with centers at A,B, and C all intersect at P.
Notice that if T is an isometry, then T
is 1:1 and onto as a function.
Proof: 1:1. Suppose that T(P)=T(Q). Then d( T(P),T(Q))=0=d(P,Q)
so P=Q.
onto. Suppose R is in the plane. Consider A,B, and C in the
plane where C is not on the line AB. Then the points T(A),T(B), and T(C)
form a triangle and using the distances d(T(A),R), d(T(B),R), and d(T(C),R),
we can determine a unique point X in the plane where d(A,X)=d(T(A),R),
d(B,X) = d(T(B),R), and d(C,X)=d(T(C),R), so T(X) = R.
Watch the video Isometries (Video
# 2576 in Library) up to the place where it is demonstrated
that the product of two reflections that have the lines of reflection
intersect at a point O is a rotation with center O through an angle twice
the size of the angle between the two lines of reflection.
Watch the remainder of the video on isometries, which classifies the
product of 3 reflections as either a reflection or a glide reflection.
| Orientation
Preserving |
Orientation
Reversing |
|
| Fixed points | Rotations | Reflections |
| No Fixed points | Translations | Glide reflections |
2. Draw a figure illustrating the effects of a central similarity on a triangle using magnification or dilation that is a) positive number >1, b) a positive number <1, and c) a negative number.
Note: The plane isometries form a group: identity, associativity,
inverses... not commutative in general.
Symmetry of a figure: S is asymmetry
of a plane figure F if
S is an isometry with S(F)=F.
Given
a figure F, the symmetries of F
form a subgroup of all the plane isometries, denoted Sym(F).
Two interesting sites for looking at symmetries are the Symmetry
Web page and the Symmetry,
Crystals and Polyhedra page.
Coordinates: (a la M&I I.3) Use any two non-parallel lines in the plane with cooincident 0. Then you can determine "coordinates" for any pont by using parallelograms. Actually all rational coordinates can be built from establishing a unit as is outlined more thoroughly in the reading in I.3.
Isometries examples in the plane: (See M&I I.5 and I.6) If T is a translation by the vector <3,5> on the coordinate plane then T(x,y)=(x+5,y+5).
If R is rotation about (0,0) by 90 degrees, then T(x,y) = (-y,x). Question: What is rotation about (0,0) by t degrees?
If F is reflection about the line Y=X, then F(x,y) = (y,x). Question: What about reflection about the line AX+BY = 0?
Start with a look at problems caused by the diagonal of a square and the issue of finding a unit that would measure both the side and the diagonal.
First look at the Euclidean algorithm for finding a common segment with which to measure two segments. The procedure appears to stop, but we can show that because of the fundamental theorem of arithmetic, it would be impossible to find a segment with which to measure both the side and the diagonal of a square. The impact of this on geometry was that one could not presume that all of geometry could be handed by using simple ratios of whole numbers for measurements. A geometry based on ratios alone would not permit one to accomplish proposition 1 of Book I of Euclid!
* Ratios exist only between magnitudes of the same type. (Homogeneity)
* For ratios to be equal the magnitudes must be capable of co-measuring.
* Euclid's axioms do not deny the existence of infinitesimals- but will not discuss equality of ratios that use them.
* It is Archimedes axiom that stays that any two segments either one can be used to measure the other. [No infinitesimals.]
Note how this might be connected to calculus: Consider the change in the area of a square when the length of a side is changed by an infinitesimal.
The connection between Euclid's definition of proportionality (equal
ratios) and real number equality of quotients.
We can show for line segments the following two propositions for segments
A,B,C,and D with m(A)=a,m(B)=b, m(C)=c, and m(D)=d:
- If A:B::C:D then a/b=c/d .
- If a/b=c/d then A:B::C:D
We can also observe that if we let S(Px)=P(x-3) then ST(Px)=S(T(Px))=S(P2x)=P(2x-3) = T*(Px), so ST=T*.
2/27More on central similarities:
In the plane a similarity T with factor m and center at (0,0) will transform
(a,b) to (ma,mb). This x' = mx, and y' = my are the equations for this
transformation.
Proposition: If l is a line in the plane with equation AX+BY=C
with A and B not both 0, then the set l' = {(x',y'): T(x,y)=(x',y')
for some (x,y) on l} is a line in the plane that is parallel to
l
(unless
l = l' ).
Proof (outline): Show that the equation of l' is AX+BY
= mC.
Mean Proportions in right triangles and Inverses: Consider a right triangle ABC with hypotenuse AB. Notice that if the altitude CD is constructed with the hypotenuse AB as the base, the figure that results has 3 similar right triangles. ABC, ACD, and DCB. Using similarity of these triangles we saw that there is a proportion of the segments of the hypotenuse AD, DB and the altitude CD given by AD:CD::CD:BD. If we consider the lengths of these segments respectively as a,h, and b then the numerical proportion may be expressed as a/h=h/b or ab=h2. Notice this says that h = sqrt(ab).
Choosing h = 1, this proportion becomes a = 1/b or ab = 1.
Construct the inverse of a point with respect to a circle a) when the point is inside the circle; b) when the point is outside the circle.
Doing arithmetic with constructions in geometry. Note that the construction above allows one to construct a point Px' from a point Px as long as x is not 0 so that x' x = 1.[ Use the circle of radius 1 with center at P0 to construct the inverse point for Px.]
In the lab we discussed how to review constructions and
watched a video (in Library #209 cass.2)
on similarity "On Size and Shape" from the For All Practical Purposes
Series.
In particular we can show that if C2 is orthogonal to C1 (with center O) and A is a point on C2 then the ray OA will intersect C2 at the point A' where A and A' are inverses with respect to the circle C1. Click here for the proof.
We can use this fact to construct a circle C2 through a given
point B on a circle C1 and a point A inside the circle so that C2 is orthogonal
to C1.
[ First construct the inverse of A' with respect to C1 and then the
tangent to C1 at B and the perpendicular bisector of AA' will meet at the
center of the desired circle.] Likewise we can construct an orthogonal
circle C2 through two points A and B inside a circle C1, as shown in the
sketch below.
[Still to be added to the notes! The correspondence between a Euclidean coordinate line and a semicircle.
The correspondence between a Euclidean coordinate line and a circle. "Continuity, inverses, and visualizing the infinite" with the semicircle + and - infinite points and the circle, a single infinite point. ]
1. Draw two intersecting circles O and O' and measure the angle between them at their point of intersection.
2. Given a circle O and two interior points A and B, construct an orthoganal circle O' through A and B. Use a measurement to show that the circles are orthogonal.
3. Draw a circle OP and an angle BAC. Use inversion with respect to the circle OP to invert <BAC to <B'A'C'. Compare the measurement of the angles. Based on this comparison, discuss briefly the effects of inversion on angles. [No proof is required here.]
- Line coordinates: The ordinary coordinates (x) corresponds to homogeneous coordinates <x,1>=<a,b> so x=a/b with b not 0. Homogeneous coordinates for a point on a line are related to lines through the origin. <a,b>=<d,e> if and only if there is some k, not 0, where d=ka and e=kb. These coordinates correspond to a line in the ordinary plane passing through (0,0). Except for the line Y=0, each of these lines has exactly one point on it of the form (x,1). A point with homogeneous coordinate <a,0> corresponds to the ideal (infinite) point on the affine line. A similar treatment works for planar coordinates.
- Plane coordinates: The ordinary coordinates (x,y) corresponds to homogeneous coordinates <x,y,1>=<a,b,c> so x=a/c and y=b/c with c not 0. A point with homogeneous coordinate <a,b,0> corresponds to an ideal point in the affine plane.
- An example of vector methods in geometry: Show that the perpendicular bisectors of any triangle meet in a single point [whiich is equidistant from the vertices].
- An introductory discussion of the role of axioms and postulates in mathematics and the sciences.
- More on the affine plane:
- An affine line in an affine plane.
- Visualizing the horizon line on an image plane.
- Homogeneous coordiates for the affine plane.
- Lab Exercise: Due 3-16.1. Draw a sketch of the affine plane showing the horizon line and label lthe lines X=1,2,-1, Y= 1,2,-1 and points (1,2) and (2,-1).
- Preface: Some examples of "structures."
- Musical structures. An atonal chord structure.
- Committee structures. A committee structure.
- Scheduling structures. A design for scheduling classes?
- Color Wheel/Triangle. (show with GSP?)
- A Geometric structure
- A graphical geometry.
- Visualizing this geometry. (GSP?)
- A Geometric structure
- A triangular geometry.
- Visualizing this geometry. (GSP?)
- Some projective geometric ideas based on a focus.
- A line through the focus appears as a point.
- A plane through the focus appears as a line.
- Two points determine a plane including the focus.
- Any two planes through the focus determine a line through the focus.
- Definitions:
- In a projective plane,
- Some algebraic descriptions of lines and planes in 3 dimensions.
- A plane through the origin has an equation of the form Ax + By + Cz = 0, where [A,B,C] is not [0,0,0]. The triple [uA,uB,uC] will determine the same plane as long as u is not 0.
- A line through the origin has the equation of the form (X,Y,Z) = (a,b,c) t where (a,b,c) is not (0,0,0).The triple (ua,ub,uc)will determine the same line as long as u is not 0.
- A P-line has an equation of the form Ax + By + Cz = 0, where [A,B,C] is not [0,0,0].
- A P-point has the equation (X,Y,Z) = (a,b,c) t where (a,b,c) is not (0,0,0).The triple (ua,ub,uc) will determine the same line as long as u is not 0.
- A P-point lies on a P line or a P -line passes through the the P-point if and only if Aa+Bb+Cc= 0 where [A,B,C] are homogeneous coordinates for the P-line and <a,b,c> are homogeneous coordinates for the P-point.
- NOTE: All of the discussion works as long as the symbols A,B,C, a,b, and c represent elements of a field, that is, a set with two operations that work like the real or rational numbers in terms of addition and multiplication.
- A field with two elements: F2 = {0,1}.
- We can visualize the projective plane using F2 using 7 points of the unit cube in ordinary 3 dimensional coordinate geometry.
2. Draw a sketch of the seven point geometry model.
A line through the focus is called a projective point (a P-point) and
A plane through the focus is called a projective line (a P-line).
A projective plane is the geometric object made up of the collection of P-points and P-lines.
any two P-points determine a unique P-line and any two P-lines determine a unique P-point.
For example, [1,0,1] determines the plane with equation X + Z = 0.
For example, (1,0,-1) deteremines the line with equation (X,Y,Z)=(1,0,-1)t.
The triple [uA,uB,uC] will determine the same plane as long as u is not 0.
We'll call [A,B,C] homogeneous coordinates of the P-line.
For example, [1,0,1] are homogeneous coordinates for the P-line determined by the plane with equation X + Z = 0.
We'll call <a,b,c> homogeneous coordinates of the P- point.
For example, <1,0,-1> are homogeneous coordinates for the P-point determined by the line with equation (X,Y,Z) = (1,0,-1) t.
For example, the P-point <1,0,-1> lies on the P-line [1,0,1].
| + | 0 | 1 | x | 0 | 1 | ||
| 0 | 0 | 1 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | 0 | 1 |
A projective plane using F2 has exactly 7 points:
A projective plane using F2 has exactly 7 lines:
This projective plane satisfies the geometric structure properties.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
Lab due Thursday 3-29. Draw sketches for each of the following triangle coincidences:
1. Medians. 2. Angle Bisectors. 3. Altitudes. 4. Perpendicular Bisectors.
The discussion reviewed the structure established for the affine and
projective planes.
In an affine plane there is a special line, the horizon or ideal,
line containing all the ideal infinite points for lines in the ordinary
euclidean plane. Any ordinary line has exactly one ideal infinite point
on it. Two lines in the ordinary plane are parallel if they do not meet.
Two lines in the affine plane are parallel if they meet at the same ideal
infinite point on the ideal line.
| Due to various pressures, I have not been
able to keep these notes current since March 13.
At this time (April 3) I can only try to keep the notes current and fill in these missing notes as time permits in the next few weeks the following topics: the definition of the algebraic model for the affine and projective plane and spaces, the connection of these geometries to visualizations, and the construction of points with corresponding coordinates in the affine line and plane using P0, P1 and Pinfinity. Fortunately, the text materials in Meserve and Izzo provides some support for these issues and should provide some support for these topics. The relevant sections are listed in the course reading assignments. Sincerely, Martin |
Lab Exercise: Due 4-6.
1. Draw a sketch for Desargue's theorem in the plane.
[Cancel problem 2. 2. Using the 3d Wingeometry,
draw a sketch of a cone with an ellipse, parabola and an hyperbola as planar
sections.]
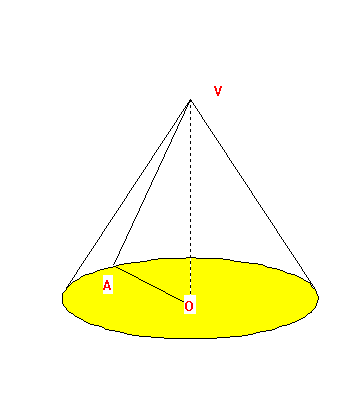
Usually we think of the point lying on the line perpendicular to the center of the circle and only the part of the cone determined by line segments from the vertex and the points on the circle. However, the cone does extend indefinitely beyond the circle and the vertex as the lines extend indefinitely. When we cut a cone with a plane not passing through the vertex we determine a curve in the plane, described as the "conic section." [If the plane passes through the vertex the interesection can be a point (the vertex itself), a single line element of the cone, or a pair of intersecting lines that meet at the vertex.] These are circles, ellipses, parabolas, and hyperbolas.
i....related to 2 foci (ellipse and hyperbola) or 1 focus (parabola),
ii...related to a focus and directrix which was also related to eccentricity.
-
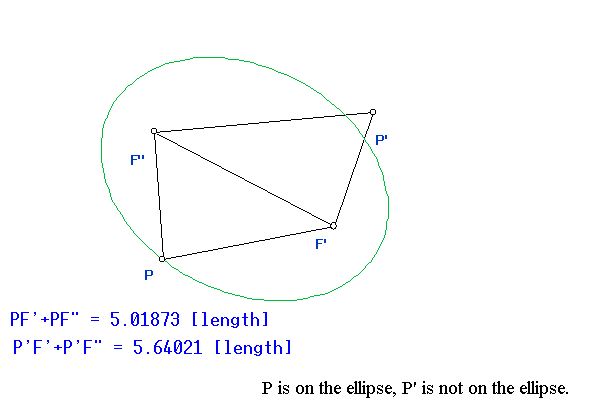
Using two spheres tangent at two focii (F1 and F2) to the sectioning plane
that also touch the sides of the cone, the ellipse is characterized by
the distance from a point on the ellipse P having the sum of the distances
PF1 + PF2 a constant,
-
Again using the spheres and choosing one of these, consider the plane through
the sphere at the circle where the sphere touched the cone. This plane
meets the sectioning plane on a line, called the directrix, d. The
film shows that for any conic section a point P on the conic is characterized
by considering the ratio of PF1 to the distance from that point to the
directrix, Pd . This ratio (called the eccentricity of the conic,
e) is a constant for each conic section, in fact the ratio of the sines
of the angle between the sectioning plane and the circle's plane and the
angle between the cone and the circle's plane.

- Notice that from the ideas of projection from the vertex of the cone, any of the conic sections could be the shadow cast by the circle on a sectioning plane.
while the hyperbola has the magnitude (absolute value) of the difference of these lengths |PF1-PF2| a constant.
 The
parabola which in a sense lies between the ellipses and hyperbolae does
not fit into these descriptions using two focii. The film explains and
visualizes these relations.
The
parabola which in a sense lies between the ellipses and hyperbolae does
not fit into these descriptions using two focii. The film explains and
visualizes these relations.
The following table summarizes the results related to this ratio. It is fully explained in the video.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In the last class, we defined the perspective relation: Two points P and P' are perspectively related by the center O if O is on the line PP" . Two triangles ABC and A'B'C' are perspectively related by the center O if O is on the lines AA', BB', and CC'.
- Desargues' Theorem: (in projective 3 space). If two non co-planar triangles ABC and A'B'C' are perspectively related by the center O, then the points of intersection P=AB*A'B'; Q=AC*A'C' ; and R=BC*B'C' all lie on the same line.
- The proof of this result in space was covered in the previous section. Recall that this relied on the intersection of the planes determined by the two triangles. In a "projective spatial geometry" any pair of distinct planes would intersect in a line.
- Notice that if we use a central projection of the spatial configuration of lines and vertices from the spatial Desargues' Theorem we have a planar configuration of lines and vertices, satisfying the same hypotheses and illustrating the same conclusion. This basic idea of projecting a result from 3-space onto the plane is used in the proof of the planar version of Desargues' Theorem as provided in the book Geometry and The Imagination by Hilbert and Cohn-Vossen.
- Desargues' Theorem: (in the (projective) plane). If two coplanar triangles ABC and A'B'C' are perspectively related by the center O, then the points of intersection P=AB*A'B'; Q=AC*A'C' ; and R=BC*B'C' all lie on the same line.
- Proof: omitted here at this time. See the handout from H&C-V.
- Comments: This theorem is a result of projective geometry in its use of the fact that any pairs of line will have a point of intersection. This can be transferred to ordinary Euclidean Geometry by using the connecting geometry of the affine plane where parallel lines meet on the ideal line. The result allows that one pair of the lines determining P,Q, or R may be parallel, but if two of the pairs are parallel, then the line deteremined by those two pairs is the ideal line, so the third point of interesection is also an ideal point. The consequence in Euclidean geometry is these special cases of Desargues' Theorem:
- Desargues' Theorem: (in the Euclidean plane). If two coplanar triangles ABC and A'B'C' are perspectively related by the center O, then either
(i) there are three points of intersection P=AB*A'B'; Q=AC*A'C' ; and R=BC*B'C' which all lie on the same line;
(ii) one pair of sides, say AB and A'B' are parallel to the line determined by the points of intersection of the other pairs of sides Q=AC*A'C' ; and R=BC*B'C';
or (iii) if two pairs of sides , say AB and A'B' are parallel and AC and A'C' are parallel, then the third pair of sides BC and B'C' are also parallel.
[Hopefully I will have a java sketch here in the future to illustrate this from the projective, affine and euclidean views in the plane.]
- More examples of proofs :
-
AB-C = AC-B
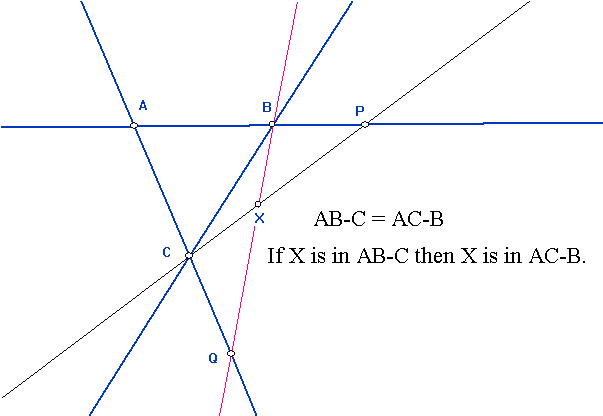
- FG is a subset of AB-C
- If F,G, and Q (not on FG) are in AB-C then AB-C=FG-Q
- Any two distinct co-planar lines intersect in a unique point. [The proof of this proposition is an exercise.]
Proof: This is a statement of set equality. By the symmetry of the equation, it will be enough to show that if X is a point in AB-C, then X is a point in AC-B. So suppose X is a point in AB-C. Then by the definition of AB-C, there is a point P on the line AB so that X is on the line PC. What is required is to find a point Q on AC so that X is on QB. Now consider the triangle PAC. B is on PA, X is on PC, so by Axiom 6, there is a point of intersection, Q where BX meets AC. End of Proof. [EOP]

This is done in two parts. (i) Show that FG-Q is a subset of AB-C.
(ii) Show that C is in FG-Q. [Then by previous work, A and B are also in FG-Q and by part (i) AB-C is a subset of FG-Q.
Proof: (i) [ to be completed....]
1. Inversion: Investigate and sketch the result of inversion on lines and circles in the plane with a given circle for inversion.
When does a line invert to a line? When does a line invert to a circle? When does a circle invert to a line? when does a circle invert to a circle? Show sketches where each case occurs. [ Remember the inverse of the inverse is the original figure.]
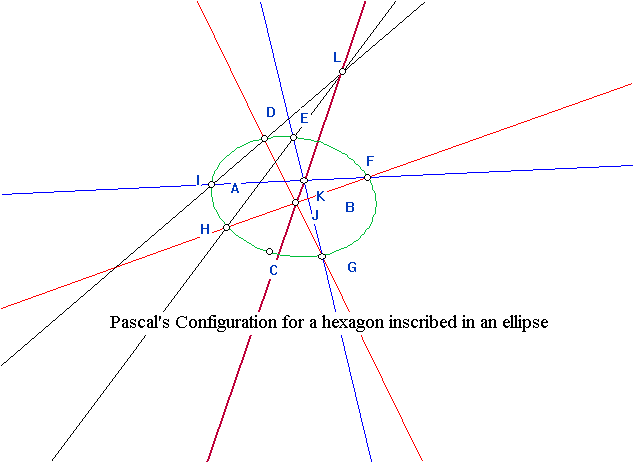
2. Pascal's configuration: Hexagons inscribed in conics. Points of intersections of opposite sides lie on a single line.
Construct a figure for Pascal's configuration with a) an ellipse , b)a parabola, and c) an hyperbola.
The term duality is used in many different mathematical contexts.In the study of planar graphs we can find an example of the use of "duality" that illustrates some of the aspects of mathematical duality. [ Other dualities: good-evil; black-white; male-female; up-down, in-out; right-left; old-new]
A planar graph consists of a finite set of points called vertices, line (straight or curved) segments with these vertices as endpoints called edges, enclosing planar sets called regions. We can think of these regions as geographic states, the edges as boundaries between land sections, and the vertices and places where these boundaries meet.
So a planar graph G is a set of vertices, edges, and resulting regions in the plane.The dual graph of G is another graph, which for now we'll denote D(G). D(G) consists of a vertex for each region in G, a region for each vertex in G, and an edge for each edge. If R is a region in G, we choose a point in R, call it r, as a vertex of D(G). For each edge, E, of G, with regions R1 and R1 bordering on E, choose an edge, e, between r1 and r2 that crosses E. Finally, suppose V is a vertex of G. consider the edges that end at V and the regions that border these edges. Then these regions and edges correspond to vertices and edges of D(G) that surround a region which we'll denote v.
The graph D(G) consists of the vertices, r, edges, e, and regions v
just described.
One aspect of the dual graph is that information about it is revealed
by knowing information about the graph G. For example, if G has 5
regions, the D(G) has 5 vertices.
If G has 7 edges then D(G) also has 7 edges, and if G has 4 vertices,
then D(G) has 4 regions.
The feature that duality exposes here in these statements is the replacement of the word "vertex" in the statement about G with the word "region" in the statement about D(G) and the word "region" in the statement about the graph G with the word "vertex" in the statement about D(G).
Duality in Plane Projective geometry:
The axioms for projective geometry in a plane uses two basic objects: points and lines, and a relation between those: a point is on a line, or a line passes through a point. The technical term for this relation is "incident", so we say a point is incident to a line and a line is incident to a point.
The dual of a statement or description in the context of a projective
plane replaces the word "point" with the the word "line" and the
word "line" with the word "point".
Here are some examples of statements and the corresponding dual statement:
| Two distinct points A and B are (incident) on a unique lineAB. | Two distinct lines a and b are (incident) on a unique point a*b. |
| If the point C is not (incident to) on the line AB then there are three lines AB, AC, and BC. | If the line c is not (incident to) on the point a*b then there are three points a*b, a*c, and b*c. |
| The lines AA', BB' and CC' are incident to the point O. | The points a*a', b*b', and c*c' are incident to the line o. |
One of the most important logical features of planar projective geometry
is connected to the duality relation. Each of the dual statements for the
postulates for planar projective geometry is a theorem of this geometry.
For example:
Postulate: Given two distinct points there is a line with those points
on it.
Dual Statement and Theorem: Given two distinct lines there is a point
with those lines on it.
As a consequence of this feature, plane projective has a special result which is about the theorems of geometry and their dual statments.
The Principle of Plane Projective Duality: Suppose S is a statement of plane projective geometry and S' is the planar dual statement for S. If S is a theorem of projective geometry, then S' is also a theorem of plane projective geometry.
The proof of this principle is a proof about proofs. The idea is that
a proof consists of a list of statements about lines and points. each statement
in a proof is either one of the postulates, a previously proven theorem,
or a logical consequence of previous statements. So if we have a proof
of a statement S, we have a sequences of statements A1,A2,...,AN=S.
Now one can construct the sequence of dual statements A1', A2', ...,
AN' = S'. With a little argument it can be seen that each of these dual
statements is also either a postulate, a theorem,or a logical consequence
of previous statements.
Here is an application of the principle of duality to Desargues' Theorem.
Since Desargue's Theorem uses the hypothesis of a perspective relation
between two triangles, we first look briefly at the dual concept.
[this will include a discussion of the dual concept for planar perspective, the statement of D's Theorem as S, the dual statement , S', and the recognition that S' is the logical converse of S. Thus we can say, "The converse of Desargues' theorem is true by the duality principle."]
review for quiz: inversion, construct P(-1) in affine geometry, hoogeneous coordinates for points, lines, intersections.
Point - plane duality... leaves line-line. This duality is more like the graph duality discussed earlier. Discussion to be completed, cube and octahedron are dual, octahedron and icosahedron are dual, the tetrahedron is dual to itself.
Postulate: the three diagonal points in a complete quadrangle do not lie on the same line. [This eleimates the 7 point geometry as a projective geometry or these axioms.
A look at perspective of planar figures with respect to a center O and
its dual: perspective of planar figures with respect to an axis o.
1. Construct a sketch showing ABC on a line perspectively related to A'B'C' on a second line with center O. 1'. Draw a dual sketch for the figure in problem 1.
2. Construct a sketch of ABC on a line projectively (but not perspectively) related to A'B'C' on a second line. Show two centers and an intermediate line that gives the projectivity. 2'. Draw a dual sketch for the figure in problem 2.
3.Construct a sketch of ABC on a line projectively (but not perspectively) related to A'B'C' on the same line. Show two centers and an intermediate line that gives the projectivity. 2'. Draw a dual sketch for the figure in problem 3.
Duality and graphs in the ordinary plane. A point is intersection of two lines, a line is the join of two points. Curves in the study of calculus are determined by points. Curves are determined by lines.
Projective relation and projectivity between points on lines (and dual) and then points on a single line.
Transformations with homogeneous coordinates of a line. Consider the isometry T of an ordinary (or affine) line with coordinates that translates a point 3 units to the right. This isometry is indicated using the ordinary coordinates by T(Px) = Px+3 or T(x) = x + 3. If we wish to understand this isometry using the homogeneous coordinates of an ordinary point we recognize that Px = <x,1>. So for an ordinary point, T(<x,1>) = <x+3,1>. Also the ideal point will be left fixed by this translation, that is, T(<1,0>) = < 1,0>. But what is the algebra for this isometry when using arbitrary homogeneous coordinates for an ordinary point? T(<a,b>) = T(<a/b, 1>) = <a/b + 3,1> = <a+3b,b>. In summary, T ( <a,b>) = <a+3b,b>.Notice this formula wrks as well for the ideal point on the affine line. This work can be done using some ideas from linear algebra. Recall that in matrix multiplication:
| [ | 1 | 3 | ] | [ | x | ] | = | [ | x+3 | ] |
| 0 | 1 | 1 | 1 |
| [ | 1 | 3 | ] | [ | a | ] | = | [ | a+3b | ] |
| 0 | 1 | b |
|
So the isometry can be considered from the point of view of algebra with homogeneous coordinates to be the result of treating the coordinates as a column vector, multiplying by a square matrix, and then using the components of the resulting column vector as the homogenous coordinates for the transformed point.
The video Orthogonal Projection was shown in the lab hour.
An overview of what we've considered so far-
| Euclidean Geometry
lines/planes |
Affine geometry
lines/planes |
Finite geometry
lines |
Projective Geometry
lines/planes |
| Axioms
Euclid Hilbert |
No Axioms Yet
A figure indicating an ideal point or line |
Axioms
7 points/7lines A figure. |
M & I Axioms
A figure indicating all points and lines |
| Parallel lines don't meet | Parallel lines meet
at an ideal point. |
All pairs of lines
have a common point |
All pairs of lines
have a common point |
| Coordinates
Analytic/Algebraic |
Ordinary coord's
w/ infinite (ideal) points Homogeneous Coordinates |
Homogeneous Coordinates
with coefficients in {0,1}= Z 2 |
Homogeneous Coordinates
with real number coefficients |
| Transformations
Isometries Similarities |
? | ? | ? |
More on projectivities. The set of projectivities can be considered
a group (as did isometries) , i.e. a set together with an operation which
satisfies certain nice algebraic properties: closure, associativity, an
identity and inverses.
4/24 More on line transformations with homogeneous
coordinates .
These transformations can be identified with matrix multiplications
since A(cv)=cAv for A a matrix, c a scalar, and v a column vector so that
pairs of homogeneous coordinates for one point are transformed to homogeneous
coordinates for a single point.
Translation: T(x)=x+3 became
| [ | 1 | 3 | ] | [ | a | ] | = | [ | a+3b | ] |
| 0 | 1 | b |
|
.. Reflection R(x)= -x uses the matrix
| -1 | 0 |
| 0 | 1 |
Dilation by a factor of 5 M(x)=5x uses the matrix
| 5 | 0 |
| 0 | 1 |
and inversion I(x)=1/x uses
| 0 | 1 |
| 1 | 0 |
Consider how composition of these transformations corresponds to matrix multiplication and how these transformations interact with the ideal point at infinity using homogeneous coordinates.
The idea of a general projective transformation of a projective line
using homogeneous coordinates and invertible 2x2 square matrices was also
introduced. We have shown now that all the transformations of the line
we had previously discussed were examples of this general type of projective
transformation.
4/26
These two topic (harmonics and projective transformations) will be a major topic for the next few weeks.
The relation between the "double points" in the figure and the "single
points". We prove using the following figure (adapted from Meserve
& Izzo) that H(RT,SU) is equivalent to
H(SU,RT). I.e., we show that if
H(RT,SU) then H(SU,RT):
The new quadrangle used to show this harmonic relation is determined
on the figure by the four points P3, P4, W and V.
[To complete the proof we need only show that WV meets SU at the point
T.]
Notice in the figure that Triangle
WP1P2 is perspectively related by the line SU to triangle VP3P4.
Thus by converse of Desargues' Theorem we have that the triangles are perspectively
related by a point. But this point must be T, so the line WV passes through
the point T, completing the demonstration that H(SU,RT).
The key issue then becomes:
Was the point constructed from the points
A, B and C uniquely determined by the fact that it was in the harmonic
relation with A, B, and C? That is, if A,B, and C are three
points on a line and D and D' are points where H(AB,CD) and H(AB,CD'),
then must D=D'? This is the question of the uniqueness of the point D.
We can prove that in fact the point D is uniquely determined.
(The proof follows the argument of Meserve and Izzo. It used Desargues' theorem several times.)
With the existence and uniqueness of the point D established,
Examples of establishing a coordinate system for a projective line
by choosing three distinct points to be P0, P1, and P¥.
We can construct P2, P-1, P1/2, (in two different ways).
Exercise: Construction P3 and P1/3.
Show that with the choice of three points on a projective line
we can construct points using harmonics to correspond to all real numbers
(as in our informal treatment of the affine line).
The following materials are from previous course notes and have not been incorporated into the current course notes.
Consider lines connecting corresponding points in a pencil of
points on a line related by a projectivity (not a perspectivity) and noticed
that the envelope of these lines seemed to be a conic, a line conic.
Notice briefly the dual figure which would form a more traditional
point conic. [Also notice how line figures might be related to solving
differential equations e.g. dy/dx=2x-1 with y(0)=3 has a solution curve
determined by the tangent lines determined by the derivative: y=x^2-x+3
which is a parabola.]
In discussing the issue of whether the 5th axiom could be proven from the other four axioms, we looked at an example of another axiom system, with an axiom N (any pair of lines having at one point in common) and an axiom P (given a line l and a point P not on that line there is a line m where P is on m and m and l have no common points) which is a version of the parallel postulate (Playfair's - not Euclid's). We gave examples showing that the four axioms and P were possible as well as the four axioms and N were possible. This showed that one can not prove axiom P or N from the other four axioms since P and N are contradictory.
By a similar analysis of the axioms for the seven point geometry we showed that it not possible prove the 5th postulate from the other four. The analysis examines the example of the seven point geometry and notices that by including an 8th and 9th point the resulting geometry would satisfy the other 4 axioms.
The model we have for affine geometry still satisfies the parallel postulate,
since the ideal (infinite) points of affine geometry are not considered
as ordinary points of the geometry. However, be removing this distinction
between ordinary and ideal points and considering the geometry that results
we obtain a geometry in which there are no parallel lines. (A projective
plane.) This will be a major focus of discussion for the remainder of the
term- especially using the homogeneous coordinates to consider points in
this geometry from an analytic/algebraic approach.
An examination of the problems of transferring an spatial image of a plane to a second plane using the idea of lines of sight we arrived at an understanding of how points in the plane would correspond to lines through a point (the eye).
In discussing the 7 point geometry we visualized it using vertices of a cube (besides (0,0,0)) with their ordinary coordinates in standard 3 dimensional coordinate geometry and identified the 7 points . This allowed us to identify "lines" using the homogeneous coordinate concepts and their relation to planes in three dimension through (0,0,0). We identified all but one of the lines easily- the last plane has ordinary equation X + Y + Z = 2... but in this arithmetic for {0,1} we have 1+1=0, so 2=0 and the vertices of that satisfy this equation in ordinary coordinates {(1,1,0), (1,0,1),(0,1,1)} form a line as well.
We then discussed using {0,1,2} for homogeneous coordinates connected to the arithmetic given by the tables
| + | 0 | 1 | 2 | * | 0 | 1 | 2 | |
| 0 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 2 | 0 | 1 | 0 | 1 | 2 | |
| 2 | 2 | 0 | 1 | 2 | 0 | 2 | 1 |
The homogeneous coordinates for this set identify ordered triples, for
example: <1,0,1>=<2,0,2> and <1,0,2>=<2,0,1>. There are
27 possible ordered triples, and thus 26 when we exclude (0,0,0), and these
are each paired by the factor 2 with another triple, so there will be exactly
13 points ( and by the comparable work with lines) and 13 lines in this
geometry.
.... some details still to be reported.
[Moved from earlier: The lab time was spent working on sketches showing ways to understand that result of the CAROMS film about the inscribed triangles of minimum perimeter.In Lab: Discuss some visual features such as trace and animation and start to look at the use of coordinates. We'll do more with coordinates, along with the use of traces and locus to see some aspects of coordinate geometry next week.]
We also watched the film on projective generation of conics which introduced
Pascal's theorem and its converse about hexagons inscribed in a conic and
showed how to use this result to construct a conic curve passing through
any 5 points. This work was also related to projectivities between pencils
of lines. We will be considering this further in the course. After a short
break we continued using metric ideas to construct an ellipse as
a locus on sketchpad and discussed how to do a parabola as well. By next
Thursday students should construct examples of the three conics on sketchpad
using metric ideas.
- Now that we've established how to connect homogeneous coordinates to a projective line using harmonics we continued by looking at some more algebraic projective lines- with coefficients of Z2, Z3, and Z5, we saw that these projective lines would have 3,4, and 6 points respectively, corresponding to the 2,3,and 5 ordinary points and one ideal point. This lead to
- A discussion of using the complex numbers, C, and the geometry of CP(1). The ordinary points on this "line" can be visualized as a plane or all the points of a sphere except one- which corresponds to the north pole or the point at infinity. [This was compared to the visualization of RP(1) as a circle.]
- The discussion turned to algebraic projective transformations of RP(1). When these leave the ideal point fixed they are called affine transformations and form a group under composition. We showed that an affine transformation has a matrix of the form
- We looked at the idea of establishing the idea of a distance between ordinary points using absolute value-
- We also looked further at Pascal's theorem and its planar dual Brianchon's theorem. Next class we'll prove Brianchon's theorem using an elliptic hyperbaloid.
| a | b |
| 0 | 1 |
and therefore T(Px)=Pax+b. Thus an affine transformation of the projective line is a dilation/reflection followed by a translation.
d( <a,b>,<c,d>) = |a/b - c/d|. We showed this is well defined and then discussed what the isometries for this distance would be. After some analysis we saw that this would mean that in the matrix of an isometry |a|=1, so a=1 or a=-1. I.e, the matrix is
| +/-1 | b |
| 0 | 1 |
or that T(Px)=P+/-x+b. Thus an isometry of RP(1) is a reflection followed by a translation.
We spent the remainder of the lecture time going over the proof of Brianchon's Theorem using the proof of Hilbert and Cohn-Vossen based on hexagons lying on the surface of an elliptic hyperbaloid (which is a ruled surface).