• Introductory Class.
  What are different aspects of geometry? How is the study of geometry organized? Analytic(numbers) , Synthetic(axiomatic),  Transformations (functions) are three ways to organize information and the study of geometry. Also Projective and Differential geometry were mentions as altenative focuses for studying geometry.
  
• Course Description.
• Additional Relevant Notes:
• Different types of geometry:
• Euclidean: Lengths are important
• Similarity: Shape is important
• Affine: Parallel lines are important.
• Projective: "Shadows" are important
• Differential: Curvature is important.
• Topological: General shape- especially holes and connectedness- is important.
• What is synthetic geometry? A geometry that focuses on connecting statements (theorems, constructions) to a foundation of "axioms" by using proofs.
• What is analytic geometry? A geometry that focuses on connecting statements (theorems, constructions) to a foundation of number based algebra.
• What is "structural geometry"? A geometry that focuses on connecting statements (theorems, constructions) to a foundation of structures (relations and operations) on sets by using proofs.
• transformations: tools that allow for changing figures:
• Euclidean: translations, rotations, and reflections.
• Similarity: magnifications, dilations
• Affine: Preserve parallel lines
• Projective:  "linear projections"...line preserving
• Differential:   "smooth".
• Topology: continuous
  

• geometry as an empirical science
• geometry as a formal system of information
• geometry focused on special objects like triangles, or special qualities like convexity.
• A figure C is called convex if given any two points in the figure, A and B, the line segment AB is a subset of the figure.
• Examples. An elliptical region in the plane is convex. A lunar region in the plane is not convex. [Here is an interesting piece of geometry related to the area of lunes.]
• Geometry on the web and using GSP and Wingeom  2D Introduction.

• Geometry has traditionally been interested in both results- like the Pythagorean Theorem- and foundations -  using  axioms to justify the result in some rigorous organization. We will be concerned with both results and foundations.
  
• We will attempt to build an understanding of both the synthetic and analytic approaches to geometry by using the tools of a structural approach.
  

• ---

   In the distinction between synthetic and analytic geometry the key connecting concept is the use of measurements. Initially we will try to avoid the use of measurement based concepts in the structures we use when possible.

• We begin  by looking at the on-line version of Euclid's Geometry- especially Book 1.
  
  • We looked briefly at the list (on-line) of initial definitions and postulates and the end results of Book I- The Pythagorean Theorem and its converse.
    We also looked are Proposition 1 and noted it had a statement that was not justified by the definitions and postulates! A more detailed discussion of this proposition is found below.
    
• We looked at the Pythagorean Theorem Activity Sheet followed by a discussion of what would we need in geometry to make a proof of the PT based on this activity.
• Back to Euclid for some further examination of the postulates:
  
  • Looking at the definitions and postulates, a key feature of any geometric structure appears early- What defines a point and a line.
  • An alternative- minimal geometry:  points: A,B.  lines: {A,B}. That's all!
  • Postulate 1. To draw a straight line from any point to any point.
  • Current view:  Two distinct points determine a unique straight line.
  • Issue: What is a "straight" line?
    
  • Alternative geometry- spherical. Points: points on a unit sphere in coordinate space: { (x,y,z): x² +  y² +  z²=1}
    Straight lines:  Great Circles on the sphere. Determined by a plane in space through (0,0,0).
    Fact: Two points on the sphere that are not antipodal- (Opposite) determine a unique straight line. [Use the plane determined by the two points and (0,0,0).] For this to make this spherical geometry satisfy Post 1- redefine what "distinct" means: If the points on the unit  sphere are antipodal, then they are considered "equal" and thus not distinct.
  
  

  ---

  • Postulate 2. To produce a finite straight line continuously in a straight line.
  • Current view: A straight line has no "endpoints".
  • Issue: What is the nature of a straight line not being "finite"?
    Alternative Geometry.  Points: all numbers in an open interval {x: 0<x<1}. Straight line: The interval (0,1) and all subintervals.
    A "finite" straight line: Any closed sub-interval of (0,1).
    Fact: Any closed sub-interval of (0,1) is properly contained in another closed subinterval of (0,1).
    Proof: Suppose 0<a,b<1. Then [a,b] is contained in the interval [a/2, (b+1)/2] which is contained in (0,1).
  • Postulate 5. That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
  • Current view: Under the given circumstances, the two straight lines are not parallel.
    Issue: How can you find the actual point where the lines meet?
    Here is the most distinctive of the postulates that appear in Euclid.
    The definition of parallel: Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.
  • Looking at "Common Notions" we see the geometry has language for equality and addition- a relation and an operation for the objects being considered.
    
    
  • Looking at how the definitions and postulates are used in Euclid:
  • Consider Euclid's Proposition 1 and  Proposition 2.
  • These propositions demonstrate that Euclid did not treat moving a line segment as an essential property worthy of being at the foundations as an axiom. However, this is a fundamental tool  for all of geometry.
  • Note that in the proof of proposition 1 the point of intersection of circles is presumed to exist without reference to any of the postulates. This presumptions was left implicit for hundreds of years, but were cleared up in the late 19th century (see the work of David Hilbert) when careful attention was given again to the axioms as a whole system.
    
    
  •  Notes on Existence: Existence is an often overlooked quality in a mathematical statement:
    For example it is common to state that sqrt(2) is an irrational number.
    The proof starts by assuming sqrt(2) is a rational number,  say sqrt(2) = p/q where p and q are natural numbers, so that ... 2 q² =  p². From this the usual proof of the statement deduces a contradiction. However, the statement assumes that there is a number the square of which is equal to 2.
    One can justify the existence of the square root of 2 in many ways. One way presumes that any line segment has a length measured by a real number. Then by the pythagorean theorem, the diagonal of a unit square will have length sqrt(2).
    
    
  • Alternative "rational coordinate" plane geometry.  [A geometry in which circles do not intersect.]
  Points: ordered pairs of rational numbers.
  
  An example of a point not in the rational coordinate plane is the point (sqrt(2),0). This point can be constructed in the ordinary plane with straight edge and compass using the circle with center (0,0) and radius determined by the points (0,0) and (1,1). This circle will meet the X-coordinate axis at the point (sqrt(2),0)
  
  The circle with center (0,0) and radius 1 and the circle with center (1,0) and radius 1 meet in the ordinary plane at the points with coordinates (1/2, sqrt(3)/2) and (1/2, -sqrt(3)/2) . Since sqrt(3)/2  is not a rational number, this ordered pair does not correspond to a point in the rational coordinate plane, so the two circles do not have a point of intersection in the rational coordinate plane.
  

• Revisit Euclid's Proposition 1 and  Proposition 2.
• Proposition 2 demonstrates a concern of Euclid about establishing a "motion" or transformation for this geometry based on fundamental postulates.
• An example of the "web" of information formed in this "axiomatic" synthetic geometry.
  
• Not just demonstrations- but the first two propositions are dedicated to constructions! A focus on existence as well as conditions that guarantee other conditions.
  

• Note that M&I build an informal presentation of a geometry structure based on using the real numbers.
  
• To explore some of these issues, let's looked at  the Pythagorean Theorem and its proofs.
•   Consider Euclid's statement and proof of Proposition 47.
In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle.

Note that Euclid's treatment in its statement or its "proof" never refers the traditional equation, a²+b²=c².


• Measurement and the Pythagorean Theorem (PT)
  

a² + b² = c²

• Pythagorean Activity Sheet
• Virtual Manipulative for PT
• Discuss Pythagorean Theorem and proofs.
• Over 30 proofs of the Pythagorean theorem!
• Many Java Applets that visualize proofs of the Pythagorean Theorem

• In one alternative proof for this theorem illustrated in the java sketch below, we consider 4 congruent right triangles and 2 squares and then the same 4 triangles and the square on the side of the hypotenuse arranged inside of a square with side "a+b" . Can you explain how this sketch justifies the theorem?

Sorry, this page requires a Java-compatible web browser. 
 
Another proof using "shearing" illustrated in the Java sketch below taken from a Geometers' Sketchpad example can be connected to Euclid's proof..
Sorry, this page requires a Java-compatible web browser. 
(Based on Euclid's Proof)  D. Bennett 10.9.9
1. Shear the squares on the legs by dragging point P, then point Q, to the line. Shearing does not affect a polygon's area.
2. Shear the square on the hypotenuse by dragging point R to fill the right angle.
3. The resulting shapes are congruent.
4. Therefore, the sum of the squares on the sides equals the square on the hypotenuse.

What kind of structures and assumptions were needed in the first proof with the triangles and squares?

Here are some considerations related to those assumptions:
• What types of objects are being considered?
• points
• lines
  
• line segments
  
• angles
• triangles
• squares
• What types of relations are being considered?
• points on lines
• Lines intersecting at points
• Congruent line segments
• congruent angles
• congruent figures (triangles, squares)
• Decomposing and recomposing a figure.
  
• How could we justify identifying "equal" objects (congruent figures)?
• How do the objects fit together?
• How do movements effect the shapes of objects.

 1. Dissections: How are figures cut and pasted together? What can be achieved using dissections?
 2. Transformations: How are figures transformed? What transformations will leave the "area" and "lengths" of figures invariant (unchanged)?

A look at the possibilities of dissections .


Puzzles and Polygons

• Tangrams. More
  
• Tangrams – Use all seven Chinese puzzle pieces to make shapes and solve problems.
  
  
  

• Cutting and reassembling polygons. More ....

• Dissections (like Tangrams) and equidecomposable polygons.
• Use tangram pieces to make a square.
• Note that in putting the pieces together to form any other shape, the area of that shape would be the same as the area of the square unless there is some overlap of the pieces in the shape.
• Question: Is this necessary condition of equal areas sufficient to say that two polygonal regions could be decomposed (cut and pasted) into smaller regions that would be congruent?

Comment: In a sense a positive (yes) response to this question means that one could create a set of smaller shapes with which one could make either of the two regions using precisely these smaller shapes. The answer to this question is yes (in fact this is a late 19th - early 20th century result), which is the basis for the remainder of this section
[The analogous problem in three dimensional geometry: volume equality of polyhedra is a necessary but not sufficient condition for a similar result. This was the third of the famous 23 "Hilbert problems" for the 20th century. This was first demonstrated by Dehn almost as son as the problem was announced. Dehn used another invariant of polyhedra related to the lengths of the edges and the dihedral angles between the faces of the polyhedra. ["Ueber den Rauminhalt," Math. Annalen, 55 (1902), 465-478].

First, consider some of the background results which were known to Euclid: (1) parallelograms results and (2) triangle results. The justifications for these results can be  reviewed briefly.

(1) a. Parallelograms between a pair of parallel lines and on the same line segment are equal (in the sense of being able to decompose one to reconstruct the other).  Proposition 35.
b. Parallelograms between a pair of parallel lines and on  congruent segments are equal (in the sense of being able to decompose one to reconstruct the other). Proposition 36.

(2) a. The line segment connecting the midpoints of  two sides of a triangle is parallel to the third side and is congruent to one half of the third side.
[The justification of this result is left as an exercise in traditional Euclidean Geometry.]
b. By rotating the small triangle created by connecting the midpoints of two sides of a triangle 180 degrees about one of the midpoints, we obtain a parallelogram. (This shows that the triangle's area is  the area of this parallelogram which can be computed by using the length of the base of the triangle and 1/2 of its altitude- which is the altitude of the parallelogram.)
Compare this with Euclid  Prop. 42 and Prop. 44.

(ii) The triangulation of any polygonal region in the plane is a key element in a proof of the equidecomposable polygon theorem.
The proof of this proposition examines a more careful characterization of the polygonal regions being considered. The key idea of the proof goes by induction on the number n = the number vertices = the number of sides in the polygon.  Proof of the triangulation proposition.

Another component of the proof of the equidecomposable polygon theorem is the ability to "add two parallelograms to form a single parallelogram which is scissors congruent to the two separate parallelograms". Here's how:
Intersect two pairs of parallel lines, l and l' with m and m'- one from each of the given parallelograms. Draw a diagonal HI in the resulting parallelogram.
Cut and translate one parallelogram so that it is scissors congruent to a parallelogram HIJK within the same parallel lines l and l' with one side being the diagonal.
Cut and translate the other parallelogram so that it is scissors congruent to a parallelogram HINO within the same parallel lines m and m' with one side being the diagonal and on the other side of the diagonal HI from the transformed first parallelogram. Now draw the parallel NO to the diagonal in the second transformed parallelogram HINO so that it intersects the parallels  l and l' from the first parallelogram at the points P and Q. This makes one larger parallelogram JKPQ which is scissors congruent to the original two parallelograms.
Compare this with  Euclid Proposition  45.

The film Equidecomposable Polygons also proves the result:
If two polygonal regions in the plane have the same area, then there is a decomposition of each into polygons so that these smaller polygons can be moved individually between the two polygons by translations or half turns (rotations by 180 degrees).
 

REVIEW of basic plane geometry concepts and definitions based on M&I.
M&I build their foundations for Euclidean geometry on a one to one correspondence between points on a line and real numbers and the ability to match angles with numbers between 0 and 180.

Sorry, this page requires a Java-compatible web browser. Sorry, this page requires a Java-compatible web browser. 

Review materials defining  rays, segments, angles, triangles, and planes  in M&I.
These definitions present a model for geometry based on the real numbers. Points, rays, line segments, etc., are identified with real numbers and intervals of real numbers. Notice that angles in the plane are not oriented and  are always considered to have a measure between 0 and 180.

Review eight of the basic Euclidean constructions described in M&I section 1.2. Note that several of these constructions rely on some foundations that assert the existence of points of intersection of circles. Thus these constructions will not be guaranteed to be effective in a geometric structure where such points do not exist- such as the geometry of the rational number plane.

Some comments about Constructions: It is important to notice that constructions also require a justification (proof) that the construction has in fact been achieved.


In proving the constructions we use some basic euclidean results, such as the congruence of all corresponding sides in two triangles is sufficient to imply the triangles are congruent (SSS). [Other basic Euclidean results are SAS and ASA congruence conditions, as well as the result that corresponding parts of congruent triangles are congruent (CPCTC).]


For these particular constructions to be justified by the same arguments given by Euclid in a geometric structure, the structure will need both an equivalence relation called congruence for line segments, angles, triangles and propositions that connect congruence of triangles to sufficient conditions  like  SSS, SAS, and ASA.
 
The constructions play two important but different roles in (euclidean) geometry:
(i) Construction allow us to "move", deconstruct and reconstruct figures, while maintaining the magnitudes of the pieces and angles . Thus constructions provide the tools for transformations such as rotations and translations.
(ii) Constructions allow us to develop comparative measurements based on a "unit" segment and the "straight" angle.

It should also be noted that the three transformations (translation, rotation, and reflection) commonly used in geometry are connected to constructions as well. For example, to translate a figure by a vector it would be useful to know how to construct parallelograms.
 
 




Note on midpoints: With the construction of midpoints in Euclidean Geometry, we can show that a Euclidean line segment has an infinite (not finite) number of distinct points. Furthermore, if we think of approximating real number distance with points on a segment after establishing a unit length, then we can construct the position of a euclidean point as close as we want to the position where a real number might correspond to a point in that position.

• The construction of points that correspond to numbers on a line.

First construct Pk where k is an integer using circles.
We can construct points with fractions using powers of 2 for the denominator by bisection.
(However, with only bisection we could not construct a point for 1/3 although we could get very close to that point using a binary representation of that common fraction.) Using  midpoints of segments we can construct points that correspond to n/2^k for any n and k. Unfortunately real numbers like sqrt(2) and pi  cannot be expressed in this way. To obtain a correspondence of points with all real numbers using bisection we need a geometric property that will give a point to correspond to any convergent sequence of numbers of the form n/2^k.

The continuity axiom for a euclidean line:
• Any non empty family of nested segments will have at least one point in the intersection of the family.
This axiom allows us to make a 1 to 1 correspondence between any real number and a point on a euclidean line once points have been determined to correspond to 0 and 1.

I.e., given P₀ and P₁   for any real number x where a<x<b there is a point P_x where P_x is between P_a  and P_b if and only if  the point Pn/2^k corresponds to the number n/2^k  for any integer n and natural number k  .

[Review the construction of a line though a given point parallel to a given line. See Euclid  I.31.]
We can also construct Pk when k is a rational number using the theory of similar triangles.

For example: We can bisect or trisect a line segment, giving us the ability to find points representing rational numbers with denominators involving powers or 2 and 3, such as 5/6, 7/18, etc.
The figure below gives two ways to achieve these constructions. One can see how to generalize these to allow one to construct points to represent any rational number on the line so that the arithmetic of numbers is consistent with the arithmetic of geometry. [Adding segments and adding numbers, etc.]

Sorry, this page requires a Java-compatible web browser.

 Consider M&I's constructions of the same correspondence of integer and rational points. These also rely on the ability to construct parallel lines.

Tangents to circles.
In considering constructions of tangents to circles we use the characterization of a tangent line as making a right angle with a radius drawn at the point it has in common with the circle. ( Book III Prop. 16.) In our construction, not Euclid's (Book III Prop. 17), we also use the result that any angle inscribed in a semi-circle is a right angle. ( Book III Prop. 31.)
Sorry, this page requires a Java-compatible web browser. 



Note on Three Historical Problems of Constructions.
(1) Trisection of an angle: Since it possible to bisect and trisect any line segment and bisect any angle, the issue is, is it possible to trisect any angle?
(2) Duplication of a cube: Since it is possible to construct a square with twice the area of a given square, the issue is, is it possible to construct a cube with twice the volume of a given cube?
(3) Squaring a circle: Since it is possible to construct a square the same area as any given polygonal region, the issue is, is it possible to construct a square with the same area as a given circle.

---


 
Doing arithmetic with constructions in geometry. Note that the construction above allows one to construct a point Px' from a point Px as long as x is not 0 so that x' x = 1.[ Use the circle of radius 1 with center at P0 to construct the inverse point for Px.]


    The relation of the inversion transformation with respect to a circle and orthogonal circles.
Proposition: If C2 is orthogonal to  C1  (with center O) and A is a point on C2 then the ray OA will intersect C2 at the point A' where A and A' are inverses with respect to the circle C1. Click here for the proof.

Solution: First construct the inverse A'  of A with respect to C1 and then the tangent to C1 at B and the perpendicular bisector of AA' will meet at the center of the desired circle.

2. Construct a circle C2  through two points A and B inside a circle C1 so that C2 is orthogonal to C1.
Solution: This solution is demonstrated in the sketch below.

Examples of using coordinates  (and Vectors) for proofs in euclidean geometry:

Proposition: An angle inscribed in a semicircle is a right angle.
Restated: If AC is the diameter of a circle and B is a distinct point on the circle, then <ABC is a right angle.

Coordinate Proof: Usingcoordinates, assume the center of the circle has coordinates (0,0) and that the point A has coordinates (1,0) and C has coordinates (-1,0) while B has coordinates (x,y) where x^2 + y^2 = 1.
To show <ABC is a right triangle by application of the converse to the pythagorean theorem it suffices to show that [(x - 1)^2 + y^2 ]+ [(x + 1)^2 + y^2] = 2^2 = 4.
This can be verified by expanding the saured terms involving x giving :   [x ^2 + 1  + y^2 ]+ [x ^2  + 1 + y^2] = 2+2 = 4. EOP.

Vector Proof: Let v be the vector from A to C and w be the vector from B to C. It suffices to show the dot product of these vectors is 0.  Now v dot w =  ( (x - 1)(x+1) + y^2 ] = x^2 - 1 + y^2  = 0. EOP.

The continuity  axiom leads to the important result due to G. Cantor that  any list (possibly infinite) of points in a given segment of a euclidean line will not have every point in that segment on the list. [Note  that we can make a list of points corresponding to the rational numbers once a unit length had been established.  1/1,1/2,2/1,1/3,2/2,3/1,1/4,2/3,3/2,4/1, ....]

The continuity axiom can also be used to prove: If a line, l, (or circle, O'A') has at least one point inside a given circle OA and one point outside the same given circle then there is of a point on the line (circle) that is also on the given circle.

Proof outline for the line-circle: Use bisection between the points on the line l outside and inside the circle OA to determine a sequence on nested segments with decreasing length approaching 0. The point common to all these segments can be shown to lie on the circle OA.

Proof outline for the circle-circle: Draw the chord between the inside and outside points on the circle O'A'. Use bisection on this chord to determine rays that by the previous result will meet the circle O'A'. The bisections can continue to determine a sequence of nested segments with decreasing length approaching 0 and with endpoints determining one outside point and one inside on O'A' . The point common to all the endpoints on the chord  will determine a point on O'A' that can be shown to also lie on OA.

Note: The circle-circle result fills in a hole in the proof of Proposition 1 in Book I of Euclid.


---

 

Recall the Definition: A figure F is convex if whenever A and B are points in F, the line segment AB is a subset of F.

The half plane example: Consider the half plane determined by a line l and a point P not on the line. This can be defined as the set of points Q in the plane where the line segment PQ does not meet the line l.  Discuss informally why the half plane is convex.

Review the problems on convex figures in Problem Set 1.

Other convex examples: Apply the intersection property [The intersection of convex sets is convex.] to show that the interior of a triangle is convex.
Show that the region in the plane where (x,y)  has y>x² is convex using the tangent lines to the parabola y=x² and the focus of the parabola to determine a family of half planes whose intersection would be the described region.

  Isometries:
Definition: An isometry on a line l /plane π /space S is a function (transformation), T, with the property that for any points P and Q,  d(T(P),T(Q))=d(P,Q) or m(PQ)=m(P'Q').

Comment: Other transformation properties can be the focus of attention- replacing isometries as the key transformation in a geometrical structure. The connection between figures and the selected  transformations is made by the fact that the transformations have a "group" structure under the operation of composition. When the transformations form a "group" there is a resulting equivalence relation structure on the figures of the geometry. This is illustrated by the relation between isometries and "congruence" in euclidean geometric structures in which distance and/or measure has a role.

Now consider Euclid's treatment of the side-angle-side congruence [Proposition 4] and how it relates to transformations of the plane that preserve lengths and angles.
Such a transformation T: plane -> plane, has T(P)=P', T(Q)=Q' and T(R)=R' with d(P,Q) = d(P',Q') [distance between points are preserved] or m(PQ)=m(P'Q')  [measures of line segments are invariant].
Review briefly the outline of Euclid's argument  for Proposition 4.
Notes:
• The Side-side-side (SSS) congruence of triangles
  (If Corresponding sides of two triangles are congruent, then the triangles are congruent)
  This allows one to conclude that any isometry also transforms an angle to a congruent angle.
• The key connection between the congruence of figures in the plane and isometries:
  Proposition: Figures F and G are congruent if and only if there is an isometry of the plane T so that T(F) = {P' in the plane where P'= T(P) for some P in F} = G.
You can read more about isometries by checking out this web site: Introduction to Isometries.


---

Some General Features of Isometries:


Proposition: If T is an isometry, then T is 1:1 and onto as a function.


Proof: 1:1. Suppose that T(P)=T(Q). Then d( T(P),T(Q))=0=d(P,Q) so P=Q.
onto. Suppose R is in the plane. Consider A,B, and C in the plane where C is not on the line AB. Then the points T(A),T(B), and T(C) form a triangle and using the distances d(T(A),R), d(T(B),R), and d(T(C),R), we can determine a unique point X in the plane where d(A,X)=d(T(A),R), d(B,X) = d(T(B),R), and d(C,X)=d(T(C),R), so T(X) = R.

• What information determines an isometry?

Proposition: For a planar isometry, T, where T(P) = P', when we know T(A), T(B), and T(C) for A,B, and C three noncolinear point , then T(P) is completely determined by the positions of A', B', and C'.

Proof: In fact we saw that T(B)=B' must be on the circle with center A' and radius= m(AB), and  T(C)= C' must be on the intersection of the circles one with center at A' and radius = m(AC) and the other with center at B' and radius = m(BC). Once these points are determined, then for any point P, P' must be on the intersection of 3 circles, centered at A', B', and C' with radii = to m(AP), m(BP), and m(CP) respectively. These three circles do in fact share a  single common point because the associated circles with centers at A,B, and C all intersect at P.


Facts: (i) If  T and S are isometries then ST is also an isometry where ST(P) = S(T(P))= S(P')  [T(P)=P'].
(ii) If T is an isometry, then the transformation S defined by S(P') = P when T(P) = P' is also an isometry.

Proof : (i) Consider d(ST(P),ST(Q)) = d( S(T(P)),S(T(Q)) ) = d(S(P'),S(Q')) = d(P',Q') = d(P,Q) .
(ii) Left as an exercise for the reader.

Comment: If G ={ T: T is an isometry of a structure}, then since Id(P)=P is an isometry, Facts (i) and (ii) together the fact that composition (product) of transformations is an associative operation make G together with the operation of composition a group structure.


---


We begin a more detailed study of isometries with a look at
Line Isometries: Consider briefly isometries of  a  line.
1) translations and 2) reflections.
How can we visualize them?


• Transformations figures (before and after lines) T: P -> P';
  
  
  
• Correspondence figures on a single line;
  
  
• Graph of transformation.
  

Coordinate function. x -> x' = f (x)
Examples: P _x -> P_x+5 a translation; P _x -> P_-x  a reflection.

Can we classify them? Is every line isometry either a translation or a reflection? Why?

Prop.: The only  isometries of the line are reflections and translations.
Proof:
Given A and A', there are only two choices for B '. One forces the isometry to be a translation, the other forces the isometry to be a reflection.
Discuss further in class.

---

Line isometries and coordinates:

Use T to denote both the geometric transformation  and the corresponding function transforming the coordinates of the points. So ... T(x) = x + 5 for the translation example and T(x) = -x  for the reflection example.
More generally, a translation T_a :P _x -> P_x+a would have T_a(x) = x + a and Reflection about the origin can be denoted R₀ , R₀(x) = -x . What about a general reflection about the point with coordinate c? R_c(x) =?  Use a translation by -c, then reflect about 0, and translate back to c. So  R_c(x) = T_c(R₀(T_-c(x))) = T_c(R₀((x -c))=T_c(-x+c)= -x + 2c.


---


Remarks on line isometries:
(i) Any isometry of a line can be expressed as the product of at most 2 reflections.
(ii) The product of two line reflections is a translation.


Now we look at Plane Isometries:
Consider isometries of  a  plane.
1) translations 2) rotations and 3) reflections.
How can we visualize them?


• Transformations figures (before and after planes); [Winplot?] [Add figures here.]
  
• Correspondence figures on a single plane; [Wingeometry]
  
• Graph? [Visualizing 4 dimensions! ]
  

Coordinate functions?
Remark: we have previously shown that an isometry of the plane is completely determined by the correspondence of three non-colinear points.


---

The classification of isometries.
There are at least four types of isometries of the plane: translation, rotation, reflection and glide reflection. [In fact , we will show that any planar isometry is one of these four types.]


• What about coordinates and plane isometries?

Coordinates: (a la M&I I.3) Use any two non-parallel lines in the plane with coincident 0. Then you can determine "coordinates" for any point by using parallelograms. [As indicated previously, all rational coordinates can be constructed from establishing a unit. This is outlined more thoroughly in the reading in I.3.]




Isometry examples with coordinates in the plane: (See M&I I.5 and I.6)

Translation: T: P _(x,y) -> P_{(x+5, y+2)} is a translation of the plane by the vector <5,2>. If we use the coordinates for the point and T(x,y) = (x',y') then x' = x+5 and y' = y+2.  We can express this with vectors <x',y'> = <x,y> + <5,2>. So translation corresponds algebraically to the addition of a constant vector.
Reflections: Across X-axis RX(x,y) = (x,-y); Across Y axis RY(x,y) = (-x,y);  Across Y=X , R(x,y)=(y,x). Notice that these can be accomplished using a matrix operation. Writing the vectors as row vectors



(x,y) ( 1 0 0 -1   ) = (x,-y)   Matrix for RX

(x,y) ( -1 0 0 1   ) = (-x,y)   Matrix for RY

(x,y) ( 0 1 1 0   ) = (y,x) Matrix for R


Or writing the vectors as column vectors



[	1	0	]	[	x	]	=	[	x	]
	0	-1			y				-y
Matrix for RX

and


[	-1	0	]	[	x	]	=	[	-x	]
	0	1			y				y
Matrix for RY

and


[	0	1	]	[	x	]	=	[	y	]
	1	0			y				x
Matrix for R


 

Rotations:
If R90 is rotation about (0,0) by 90 degrees, then R90(x,y) = (-y,x).
Question: What is rotation about (0,0) by t degrees: R(t)?
Hint: What does the rotation do to the points (1,0) and (0,1)? Is this rotation a "linear transformation?"
More general Question: What about reflection R(A,B) about the line AX+BY = 0?


[ 0 -1 ] [ x ] = [ -y ] 1 0 y x Matrix for R90

[ a b ] [ x ] = [ ax+by ] c d y cx+dy R(t):Matrix for rotation by t degrees?  Hint: Consider that P(1,0) will be transformed to  P'(cos(t), sin(t))= (a,c)  and Q(0,1) will be transformed to  Q'(-sin(t), cos(t))=(b,d)

[ a b ] [ x ] = [ ax+by ] c d y cx+dy Matrix for R(A,B)?

Proposition: Any plane isometry  is either a reflection or  the product of two or three reflections.
Proof: Click here!

---


Rotations and reflections [review +]:
More general Question: What about reflection R(A,B) about the line AX+BY = 0?


[ cos(t) -sin(t) ] [ x ] = [ xcos(t)-ysin(t) ] sin(t) cos(t) y xsin(t)+ycos(t) R(t):Matrix for rotation by t degrees. See discussion above.

[ a b ] [ x ] = [ ax+by ] c d y cx+dy Matrix for R(A,B)?  Hint: Rotate, reflect, and rotate back! Composition of Isometries corresponds to Matrix multiplication!

If B = 0 then the line of reflection is the Y axis and we know the matrix for RY already. For all other B, let t be the angle which has tan(t) = - A/B. Thus the reflection R(A,B) has a matrix that must be the product [from left to right]of the matrices for  R(t), RX, and R(-t).

Before Reflection	After Reflection

More General Planar Isometries:
A key idea is do the work at the origin and then transfer the work elsewhere using "conjugacy":  Any transformation T at a general point or about a general line can be investigated by first translating the problem to the origin, S, performing the related transformation at the origin,T',  and then translating the result back to the original position, S^-1. That is using the "conjugacy" operation: T = S^-1 T' S  where T' is the relevant transformation at the origin.  This works as well for rotation and reflections through the origin because the composition of these transformations corresponds to matrix multiplication.


Here is a link to an example of the matrix for the isometry of the coordinate plane that is rotation by 90 degrees counterclockwise about the point (1,2). 

Proposition:
(i) The product of two reflections that have the lines of reflection intersect at a point O is a rotation with center O through an angle twice the size of the angle between the two lines of reflection.

(ii) The product of two reflections that have parallel lines of reflection is a translation in the direction perpendicular to the two lines and by a length twice the distance between the two lines of reflection.

(iii) The product of three reflections is either a reflection or a glide reflection.

Proof: We can do this geometrically or using analytic geometry and the matrices!

Watch the video Isometries (Video # 2576 in Library) . 

• Note: The four types of isometries can be characterized completely by the properties of orientation preservation/reversal and the existence of fixed points. This is represented in the following table:

	Orientation  Preserving	Orientation  Reversing
Fixed points	Rotations	Reflections
No Fixed points	Translations	Glide reflections

---

Note: The plane isometries form a group: A set together with an operation (the product or composition) that is
(0) Closed under the operation - the product of two isometries is an isometry;
(1) The operation is associative - R(ST) = (RS)T  or for any point P,  (R(ST))(P) = R( ST(P))= R(S(T(P))) = (RS)(T(P)) = ((RS)T)(P).
(2) The identity transformation (I) is an isometry -  I(P)=P.
(3) For any isometry T there is an (inverse) isometry S so TS = ST = I.
The operation of composition is not necessarily commutative in the sense that ST is not always the same transformation as TS:
For example If R1 and R2 are reflections in intersecting lines l1 and l2 then the isometry R1R2 is a rotation about the point of intersection in the opposite direction to R2R1.

---

 An Applications of Reflection:
(i) Here is a problem  encountered frequently in first semester of a calculus course.
The Carom Problem Can you see how the solution is related to a "carom" (angle of incidence=angle of reflection)?
 (ii) Here is a similar problem about triangles that is also related to reflections.
Fano's Problem  Can you find the relationship?


---

  Symmetry of a figure: S is a symmetry of a plane figure F  if S is an isometry with S(F)=F. Given a figure F, the symmetries of F form a subgroup of all the plane isometries, denoted Sym(F).
Example: Consider the figure F= an given equilateral triangle. We looked at the six symmetries of this figure and the table indicating the multiplication for these six isometries.






The Group Table of Symmetries of an Equilateral Triangle.

R*C	I	R120	R240	V	R1	R2
I	I	R120	R240	V	R1	R2
R120	R120	R240	I	R2	V	R1
R240	R240	I	R120	R1	R2	V
V	V	R1	R2	I	R120	R240
R1	R1	R2	V	R240	I	R120
R2	R2	V	R1	R120	R240	I

Two interesting sites for looking at symmetries are the Symmetry Web page  and the Symmetry, Crystals and Polyhedra page.
• Discussion: What about isometries in three dimensions?

These are generated by spatial reflections in a plane.
A spatial isometry is determined by the transformation of 4 points not all in the same plane (which determine the simplest 3 dimensional figure- a tetrahdron!)
Any isometry of space can be expressed as the product of at most 4 reflections.
These results are proven in the same fashion as the comparable results were proven in the plane.


---

• Proportions and similarity:

A look at problems caused by the diagonal of a square and the issue of finding a unit that would measure both the side and the diagonal.
First look at the Euclidean algorithm for finding a common segment with which to measure two segments.
Euclid's original treatment of the "division algorithm" :
If  n and d>0 are integers
then there are integers q and r with r=0 or 0<r<d where n = q*d +r.

Using q*OD to represent a segment that is made of q segments all congruent to OD,
Euclid's division algorithm is stated in geometry that of ON is a segment and OD is a segment that is contained as a subsegment of ON, then ON is congruent to q*OD  with  possibly a remaining segment RN which is congruent to a subsegment of OD.

Repeated use of this algorithm suggests the Euclidean algorithm for finding a common unit to measure both n and d, or ON and OD.


If r1=0 or R1N is a point, then OD will be a common unit.
If not apply the division algorithm to d or OD and r1 or R1N.
If this works to give r2= 0 or R2N is a point, then R1N will be the common unit. 
If not apply the division algorithm to r1 or R1N and r2 or R2N.
If this works to give r3= 0 or R3N is a point, then R2N will be the common unit.
If not continue.
In common arithmetic since each remainder that is not zero is smaller than the previous remainder, eventually the remainder must be 0 and the process will end- finding a common divisor of the original d and n.
 

In the application of the euclidean algorithm to the diagonal and side of a square, the procedure appears to stop.
However, we can show that because of the fundamental theorem of arithmetic, it would be impossible to find a segment with which to measure both the side and the diagonal of a square.

The impact of this on geometry was that one could not presume that all of geometry could be handled by using simple ratios of whole numbers for measurements.

[A geometry based on ratios alone would not permit one to accomplish proposition 1 of Book I of Euclid! since this would mean that the geometry would have to be able to have ratio involving the sqr(3) - which like the sqr(2) is also an irrational number.]

---

  A major part of geometry before Descartes was Euclid's (Eudoxus') resolution of the issue in Book V def'ns 1-5.(Joyce)

Definition 1

A magnitude is a part of a magnitude, the less of the greater, when it measures the greater.

Definition 2

The greater is a multiple of the less when it is measured by the less.

Definition 3

A ratio is a sort of relation in respect of size between two magnitudes of the same kind.

Definition 4

Magnitudes are said to have a ratio to one another which can, when multiplied, exceed one another.

Definition 5 (Byne's)

Magnitudes are said to be in the same ratio, the first to the second and the third to the fourth, when,
if any equimultiples whatever are taken of the first and third,
and any equimultiples whatever of the second and fourth,
the former equimultiples alike exceed, are alike equal to, or alike fall short of, the latter equimultiples respectively taken in corresponding order.




Look at these definitions and note some key items:
* Ratios exist only between magnitudes of the same type. (This is usually described as "Homogeneity".)
* For ratios to be equal the magnitudes must be capable of co-measuring.
* Euclid's axioms do not deny the existence of infinitesimals- but will not discuss equality of ratios that use them.

Briefly: An infinitesimal segment is a segment AB that is so short that it would appear to be coincident points and for any k, k*AB cannot contain any ordinary segment determined by points that we can see as distinct!
In the history of mathematics, infinitesimal segments we used in the early developments of the calculus. For example: Consider the ratio of {the change in the area of a square, A(s), when the length of a side, s, is changed by an infinitesimal, ds} to {the change in the length of the side, ds}. That is: What is [A(s + ds) - A(s)]/ds ?  Answer: [2s*ds + ds*ds]/ds = 2s +ds. Thus the ratio would be indistinguishable as a number from 2s. ]

* The  Axiom of Archimedes that says that for any two segments one can be used  to measure the other. [There are no infinitesimals for an Archimedean geometry.]

Example: Euclid uses the theory of proportion in Book VI, Proposition 1 and Proposition 2.
(see also Byrne's Prop.1  and Prop.2.)


---

The connection [between Euclid's definition of proportionality (equal ratios) and real number equality of quotients].
We can show the following
Proposition: For segments A,B,C,and D with m(A)=a,m(B)=b, m(C)=c, and m(D)=d:
1. If A:B::C:D then a/b=c/d .
2. If a/b=c/d then A:B::C:D
Proof.
 

• The concept of similarity as a transformation.

Euclidean Constuction for a Central Similarity:

Proposition 1 (Book VI) of Euclid provides the tool for the central similarity transformation in Euclidean geometry.  To perform the transformation of the plane with center O and using two given line segments to determine the magnification, first draw a ray from O and locate P and P' on the ray so the given segments are congruent to OP and OP'. To transform a point Q
draw the ray OQ, then the segment PQ. Through P' construct a line l that is parallel
to PQ. Then l will meet OQ at a point Q' and by proposition 1, Q' is the appropriate point to which Q is transformed by the central similarity as required.

It is not difficult to show from this construction that a central similarity will transform a line  l to a line l' that is parallel to the original line l. Thus one can prove the related results for euclidean geometry:
Corollary: If T is a central similarity then
(i) T preserves the measure of angles and
(ii) T transforms a pair of parallel lines to parallel lines.

Since isometries also preserve the measure of angles and transform a pair of parallel lines to parallel lines (since a reflection does) we see that any composition of central similarities and isometries will likewise preserve the measure of angles and transform a pair of parallel lines to a parallel lines. 
Exercise: Show such compositions will transform a triangle to a similar triangle and ABC and A'B'C' is any pair of similar triangles, the there is an isometry T and a central similarity S so that TS transforms ABC to A'B'C'.

Similarity Transformations in Coordinate Geometry.
Consider a similarity on a line with a center of similarity and a given positive magnification factor. This leads to a consideration of the effect of a similarity on the coordinates of a point on the line.
If we use the point P0 for the center, then we see that the similarity T with magnification factor of 2 would transform Px to P2x, or T(Px)=P2x. Removing the P from the notation we have T(x)=2x. Using T(Px)=Px', we find that T is described by the correspondence where x'=2x.

[More generally: If we use the point P0 for the center, then we see that the similarity T with magnification factor of m would transform Px to Pmx, or T(Px)=Pmx. Removing the P from the notation we have T(x)=mx. Using T(Px)=Px', we find that T is described by the correspondence where x'=mx. ]

With the center at another point, say P3, the transformation T* is controlled by the fact that T*(Px) - P3 = 2(Px-P3).
So that  for T* we have x' = 3 + 2(x-3).

[Again generally: With the center at point Pa, the transformation T* is controlled by the fact that T*(Px) - Pa = m(Px-Pa). So that  for T* we have x' = a + m(x-a).]



We can also observe that if we let S(Px)=P(x-3) and S^-1(Px)=P(x+3) then

S^-1(T(S(Px))) = S^-1(T(P(x-3)))
= S^-1(P2(x-3))
= P(3+2(x-3))
= T*(Px), so S^-1TS=T*.

---


Central similarities in the plane:
In the plane, a similarity Tm  with factor m and center at (0,0) will transform  (x,y) to (mx,my). Thus x' = mx, and y' = my are the equations for this transformation. This transformation can be represented using a matrix as follows:


[	m	0	]	[	x	]	=	[	mx	]
	0	m			y				my
Matrix for Tm

Other central similarities T* with factor m and center at (a,b) can be recognized as related to Tm by using the translation S(x,y) = (x - a,y - b) and seeing that  S^-1TmS=T*.
[Try this yourself!]

Proposition: If l is a line in the plane with equation AX+BY=C  with A and B not both 0, then the set l' = {(x',y'): Tm(x,y)=(x',y') for some (x,y) on l} is a line in the plane that is parallel to l (unless l = l' ).
Proof (outline): Show that the equation of l' is  AX+BY = mC. Suppose (x,y) satisfies the equation AX+BY=C. Then Tm(x,y) = (mx,my).  But Amx+Bmy=m(Ax+By)=mC, so the line l ' has equation AX+BY=mC, and therefore is parallel to the line l.

 We can use coordinate geometry to describe a central similarity S of factor 5 with center at (3,2)  as  follows: (x,y) -> (x - 3,y - 2) -> (5(x -3) ,5(y - 2))  -> (5(x -3) +3 ,5(y - 2) +2).
Thus S(x , y) = (5x -12 ,5y - 8).
Here is the visualization of S(x,y) as a map in Winplot:

S(x , y) = (5x -12 ,5y - 8).

Before

After

---


View video (in Library #4376 ) on "Central similarities" from the Geometry Film Series. (10 minutes)
View video (in Library #209 cass.2) on similarity (How big is too big? "scale and form")  "On Size and Shape"  from the For All Practical Purposes Series. (about 30 minutes)


---


Mean Proportions in right triangles and Inverses: Consider a right triangle ABC with hypotenuse AB. Notice that if the altitude CD is constructed with the hypotenuse AB as the base, the figure that results has 3 similar right triangles. ABC, ACD, and DCB. Using similarity of these triangles we see that there is a proportion of the segments of the hypotenuse AD, DB and the altitude CD given by AD:CD::CD:BD. If we consider the lengths of these segments respectively as a,h, and b then the numerical proportion may be expressed as a/h=h/b or using common algebra ab=h². Notice this says that h = sqrt(ab).
 

Sorry, this page requires a Java-compatible web browser.

Application of this construction:
1. Choosing a = 1, this proportion becomes h = sqrt(b)
2. Choosing h = 1, this proportion becomes a = 1/b or ab = 1.
 
• Note: Since ab=h², the construction of the segment with length h solves the problem of constructing the side of a square which has the same area as a rectangle with sides of length a and b. So we can square a rectangle with straight edge and compass tools. (See the three historical problems of constructions and the dissection theorem discussed earlier.)
• The arithmetic mean of two segments of length a and b is a segment of length m with the property that  m - a = b - m,  so that a+b = 2m.

The geometric mean  of two segments of length a and b is a segment of length h with the property that h/a= b/h or ab=h²

• ---

  
  
• This brings up again the concept of inverses of points with respect to a given circle and the construction of inverses. These are  connected to the similar triangles just mentioned showing that the constructions in M&I 1.3 were correct.
• Here is one construction of an inverse using the previous facts about similar right triangles.

Sorry, this page requires a Java-compatible web browser.


---

And here is the construction as given in Meserve and  Izzo with x > 1.

Sorry, this page requires a Java-compatible web browser. 

---

In this structure we consider all points and lines in the usual plane with the exception of one special line designated as the "horizon" line. Points on this line is not considered as a part of the geometrical points but are used in defining the class of parallel lines in the reamining plane.
A line in this structure is any line in the original plane with the exception of the horizon line. 
Two lines are called A-parallel (A for affine) if (i) they are both parallel in the usual sence to the horizon line or (ii) they have a point in common that lies on the horizon line.
At this stage we do not have a correspondence for points in this plane and real number coordinates.
We can consider a figure to illustrate this geometry as below:

---

•   Separate notes on the Affine line and Plane.


These notes describe such issues as
• The correspondence between a Euclidean coordinate line and a semicircle.
•  The correspondence between a Euclidean coordinate line and a circle.
• How to see an infinite (ideal ) point on a line.
•  How to see infinite points in the plane.

---

Homogeneous coordinates for an affine line.
• Seeing the ordinary coordinate system in the affine plane.
• and more!

"Continuity, inverses, and visualizing the infinite"


• Homogenous coordinates for an affine line or plane (in 1 and 2 dimensions).
• Line coordinates: The ordinary coordinate (x)  for a point Px corresponds to homogeneous coordinates <x,1>=<a,b> so x=a/b with b not 0. Homogeneous coordinates for a point on a line are related to lines through the origin. <a,b>=<d,e> if and only if  there is some k, not 0, where d=ka and  e=kb. These coordinates correspond to a line in the ordinary plane passing through (0,0). Except for the line Y=0, each of these  lines has exactly one point on it of the form (x,1). A point with homogeneous coordinate <a,0> corresponds to the ideal (infinite) point on the affine line. A similar treatment works for planar coordinates.

  ---

Plane coordinates: The ordinary coordinates (x,y) corresponds to homogeneous coordinates <x,y,1>=<X,Y,Z> so x=X/Z and y=Y/Z with Z not 0. A point with homogeneous coordinate <X,Y,0> corresponds to an ideal point in the affine plane.
[See Winplot sketches from RP2inR3.wp3]



A line in the Euclidean plane corresponds to an equation relating the ordinary coordinates of points on the line.

For example, 3x - 5y = 1.  To understand this line in the Affine plane we consider points with homogeneous coordinates <X,Y, Z> that satisfy the equation: 3X - 5Y = Z  or  3X - 5Y - Z = 0.




Notice that using  the coordinates <x,y,1> we can see the relation between the equation for the line in ordinary coordinates and the equation for the line in homogeneous coordinates.
The equation 3X - 5Y - Z = 0 is described as a homogeneous linear equation.


---

• Assigned: Watch video related to axioms for geometry (especially the parallel postulate), The Open University video, "A non-Euclidean Universe." (#346)

• ---

• An introductory discussion of the role of axioms and postulates in mathematics and the sciences.

In the history of geometry, there have been two main approaches to the nature of the postulates or axioms for geometry.
1. The postulates are a part of an attempt to model the reality of measurements on planes and in space. They are a convenience that allows one to verify only a few limited statements in the modelling process and then deduce from those postulates other properties of the reality of the model. Under this view, geometric axioms might be considered similar to other scientific statements that are supposed to reflect in a platonic world what we find in the empirical world of reality.

2. Axioms provide linguistic and mathematical structures useful for developing further logical relations that can be used to understand a variety of contexts in some abstraction efficiently. An example of such a view of axioms is found in the axiomatic description of a vector space and the study of  abstract vector spaces, which can be modelled in the physics view of vectors as things with magnitude and direction, or in as abstract a setting as the collection of all real valued functions on a given set S.

3. We have seen examples of axioms and postulates in Euclid's Elements and Hilbert's axioms listed in the video.


---

• Note: Descartes' geometry: Algebra constructions for products and quotients.
  
• Here are some examples of "structures" in a variety of settings.
• Musical structures. An atonal chord structure.
• Committee structures. A committee structure.
• Scheduling structures. A design for scheduling classes?
• Color Wheel/Triangle. (show with GSP?)
• A Geometric structure
• A triangular graphical geometry.

---




Connecting Axioms to models.

---

Informal projective geometry and algebra 

Projective Geometry with a field with two elements: 
Another model for the 7 point geometry.
Z₂ = F₂ = {0,1}.

+	0	1			*	0	1
0	0	1			0	0	0
1	1	0			1	0	1

A projective plane using F₂ has  exactly 7 points: <0,0,1>, <0,1,0>, <0,1,1>,<1,0,0>,<1,0,1>,<1,1,0>,<1,1,1>.

A projective plane using F₂ has exactly 7 lines: AX + BY +CZ = 0  or [A,B,C] is a line using homogeneous coordinates.

[0,0,1], [0,1,0], [0,1,1], [1,0,0], [1,0,1], [1,1,0], [1,1,1].


---

Note that <x,y,z> is a point on [A,B,C] if and only if using the vector dot product:  (x,y,z)(A,B,C) = 0


This projective plane satisfies the geometric structure properties described previously in the "7 point geometry".
This can be verified using the following table where an X indcates the point of the column is an element of the line of the row.

Lines\Points	<0,0,1>	<0,1,0>	<0,1,1>	<1,0,0>	<1,0,1>	<1,1,0>	<1,1,1>
[0,0,1]		X		X		X
[0,1,0]	X			X	X
[0,1,1]			X	X			X
[1,0,0]	X	X	X
[1,0,1]		X			X		X
[1,1,0]	X					X	X
[1,1,1]			X		X	X

• We can visualize the projective plane  using F₂ with the 7 points of the unit cube in ordinary 3 dimensional coordinate geometry.


---

In doing this, many of the lines do correspond to planes through the origin in the usual geometry, such as [1,0,0] ( X=0) , but others look a little strange because the use the arithmetic of  Z₂ , such as  [1,1,1] (X+Y+Z=0) which has on it the three point <0,1,1>, <1,0,1> and <1,1,0> which does not appear to be a plane through the origin (0,0,0).

• Informal projective geometry and algebra 
•  Models for geometry using algebra and coordinates for euclidean and affine geometry especially equations for lines.
• We define a perspective relation:
  Two points P and P' are perspectively related by the center O if O is on the line PP" . Two triangles ABC and A'B'C' are perspectively related by the center O if O is on the lines AA', BB', and CC'.
  
   
• Another aspect of Projection: Desargues' Theorem in 3-space and the plane.
  

---


Review of the distinctions in our informal discussion of euclidean, affine and projective geometry.
 

Euclidean Line: P0 and P1  Euclidean Plane: P(0,0), P(1,0), and P(0,1).  Axes at right angles.  Parallel lines have no point in common.

Affine Line: P0, P1, and Pinf.  Affine Plane: P(0,0)=<0,0,1>, P(1,1)=<1,1,1>,P(inf,0)=<1,0,0>, P(0,inf)=<0,1,0>  The Horizon or Ideal line.  Parallel lines meet at an infinite point on the horizon.

Projective Line: Pinf is treated as an ordinary point. A circle.  Projective plane: All points in the affine plane are treated as ordinary points. Homogenous coordinates determine all points and lines.  There are no parallel lines. All lines meet.

In an affine plane constructions using parallel lines in the euclidean plane can be performed using the horizon line to determine appropriate parallel lines in the constructions. This was demonstrated by constructing P(1,0) and P(2,0). 

---

The structure established so far for the affine and projective planes.
In an affine plane there is a special line, the horizon  or ideal, line containing all the ideal infinite points for lines in the ordinary euclidean plane.
Any ordinary line has exactly one ideal infinite point on it.
Two lines in the ordinary plane are parallel if they do not meet.
Two lines in the affine plane are parallel if they meet at the same ideal infinite point on the ideal line.
 In the projective plane there are no parallel lines! 


---

---

Reconsider how we model geometry visually and algebraically:
 

	Visual	Algebraic
Euclid		Points:Ordinary coordinates(x,y)  Lines: Ax+By+C=0
Affine		Points: Ordinary (x,y) or generally homogeneous <x,y,z> x,y,z not all 0.  Lines: Ax+By+C=0 or Ax+By+Cz = 0 or [A,B,C]
Projective		Points: <x,y,z> x,y,z not all 0.  Lines:  Ax+By+Cz = 0 or [A,B,C] A,B,C not all 0.

• The Synthetic Projective Plane can be modelled by the corresponding visual and algebraic concepts.
  

  ---

• Postulates from M&I:
1. There exists at least one line.
2. There are at least three distinct points on each line.
3. If A and B are any two distinct points, there is at least one line AB on both A and B
4. If A and B are any two distinct points, there is at most one line AB on both A and B.
5. Not all points are on the same line.
6. If a line intersects two sides of a triangle and does not contain a vertex of the triangle, then the line intersects the third side of the triangle.

Some simple consequences of these postulates: [See M&I for proofs.]
Theorem 4.1: If A and B are any two distinct points, there is one and only one line AB on both A and B.
Theorem 4.2: A line is determined by any two of its points.

Definition: If A,B and C are three distinct points with C not on the line AB, then the triangle ABC is the set of points A,B,and C and lines AB, AC, and BC, i.e., triangle ABC = { A,B,C, AB, AC, BC}.

Definition:If A,B and C are three distinct points with C not on the line AB, the plane AB-C is the set of all points on the lines  PC for any point P on the line AB.

This lecture discussed homogeneous functions and in particular how a circle and a parabola would be described with homogeneous coordinates.
More details on this lecture will be supplied at a later time.

Examples: Two points determine a line:


Visually: Two ordinary points determine an ordinary line. An ordinary point and an ideal point determine and ordinary line. Two ideal points determine the horizon line.

Algebraically:
The problem is to determine A, B, and C so that

 Ax1+ By1+Cz1=0 and
Ax2+ By2+Cz2=0     

where <x1,y1,z1> and <x2,y2,z2> are distinct points, so that they are not scalar multiples of each other. 

But this means we have have two homogeneous linear equations  with unknowns A,B,C.
By elementary linear algebra this system will have a family of solutions determined by a single parameter.
Thus any two solutions A,B, C and A',B',C' will have a scalar t, not zero, with A'=tA, B'=tB, and C'=tC.
So there is a unique line [A,B,C] determined by the two points.


• The 6th axiom from M&I .
  Visually: This axiom can be seen to justify the statement that there are no parallel lines in the visual model for this geometry. From a euclidean viewpoint: This can be understood, since any pair of parallel lines can be organized to be the base and the line connecting midpoints of a triangle. But Axiom 6 says that the line determined by midpoints  of a triangle must meet the third side, so it cannot be parallel to the base!
• From the algebraic model the 6th Axiom  is also true.
  If
  
  Ax +  By + Cz = 0 and
   A'x + B'y + C'z = 0        
  
• are two distinct lines in the projective plane,  then there are non-trivial solutions (x,y,z) to this pair of homogeneous linear equations.
  These solutions will be on a line through (0,0,0), so any non-trivial solution will determine the homogeous coordinates for a point <x,y,z> lying on both lines. 

  ---

  
  

Where we're going in the next few weeks. We will be discussing the following topics: the definition of the algebraic model for the affine and projective plane and spaces, the connection of these geometries to visualizations, and the construction of points with corresponding coordinates in the affine line and plane using P0, P1 and Pinfinity. The text materials in Meserve and Izzo provides support for these  issues and topics. The relevant sections are listed in the course reading assignments.

• Notation: We'll use the notation RP(2) = { <x,y,z> : x,y,z real numbers and not all zero}. <x,y,z>=<x',y',z'> means there is a non-zero number t so that x'=tx, y'=ty, and z'=tz.

Similarly RP(3)= { <x,y,z,w> : x,y,z,w real numbers and not all zero}.
<x,y,z,w>=<x',y',z',w'> means there is a non-zero number t so that x'=tx, y'=ty, z'=tz and w'=tw.

Likewise Z₂P(2) ={ <x,y,z> : x,y,z in {0,1}and not all zero}
                           = { <0,0,1>,<0,1,0>, <0,1,1>,<1,0,0>, <1,0,1>, <1,1,0>, <1,1,1>}.
Of great interest to research mathematicians currently is
CP(2)={ <x,y,z> : x,y,z complex numbers and not all zero}.
<x,y,z>=<x',y',z'> means there is a non-zero number t so that x'=tx, y'=ty, and z'=tz.

Notice that { <x,y,z> in RP(2) where x² + y² + z²  = 0} is an empty set,
whereas <i,0,1> is a member of the comparable set { <x,y,z> in CP(2) where x² + y² + z²  = 0} because this set allows the use of complex numbers such as i.



---

• Coincidences: Many results in projective geometry are stated as coincidences... as the Theorem of Desargues' had three points all lying on the same line.

Here is a traditional euclidean geometry coincidence theorem:
(Compare this with the vector proof given previously.)
• Theorem. The perpendicular bisectors of any triangle all pass through the same point.

Proof

---

• A continuation of the synthetic (axiomatic) development of Projective 2 and 3 Dimensional Geometry following M&I Chapter 4.
• 
• More examples of proofs : [See M&I for the definition of AB-C.]
• Proposition: AB-C = AC-B
Proof: This is a statement of set equality. By the symmetry of the equation, it will be enough to show that if X is a point in AB-C, then X is a point in AC-B. So suppose X is a point in AB-C. Then by the definition of AB-C, there is a point P on the line AB so that X is on the line PC. What is required is to find a point Q on AC so that X is on QB. Now consider the triangle PAC. B is on PA, X is on PC, so by Axiom 6, there is a point of intersection, Q where BX meets AC.  End of Proof. [EOP]

---

• Proposition: If F and G are points in AB-C then FG is a subset of AB-C
Proof: Suppose X is on the line FG with F and G in AB-C.
Since F is in AB-C, there is a point P on AB where F is on PC.
Also by work done previously, we have shown that FG intersects AB at a point Q.
To show that X is in AB-C, it is enough to show that XC meets AB (at the point R). So consider the triangle PQF. X is on FQ, C is on PF, so by Axiom 6, XC meets PQ. But PQ = AB. EOP.

• If F,G, and Q (not on FG) are in AB-C then AB-C=FG-Q

This is done in two parts. (i) Show that FG-Q is a subset of AB-C.
(ii) Show that C is in FG-Q. [Then by previous work, A and B are also in FG-Q and by part (i) AB-C is a subset of  FG-Q.
Proof:
(i) Suppose X is FG-Q. Then there is a point Z  on FG and XQ.

So Z is in AB-C (being on FG) and X is on ZQ (which is in AB-C), so X is in AB-C. Thus FG-Q is a subset of AB-C.
(ii) Left as an exercise. [Hint: Use Postulate 6 to find a point on CQ intersect FG.]



---

• Proposition: Any two distinct co-planar lines intersect in a unique point. [The proof of this proposition is an exercise.]

---

•  Proof of Desargues' theorem in the projective plane. [Based on the spatial version of D.T. already proven.] 

  ---

• Planar duality and the Converse of Desargues' theorem in projective geometry.

Duality in Plane Projective geometry:

The axioms for projective  geometry in a plane uses two basic objects: points and lines, and a relation between those: a point is on a line, or a line passes through a point. The technical term for this relation is "incident", so we say a point is incident to a line and a line is incident to a point.

The dual of a statement or description in the context of a projective plane  replaces the word "point" with the the word "line" and the word "line" with the word "point".
Here are some examples of statements and the corresponding dual statement:  

Two distinct points A and B are (incident) on a unique lineAB.	Two distinct lines a and b are (incident) on a unique point a#b.
If the point C is not (incident to) on  the line AB then there are three lines AB, AC, and BC.	If the line c is not (incident to) on  the point a#b then there are three points a#b, a#c, and b#c.
The lines AA', BB' and CC'  are incident to the point O.	The points a#a', b#b', and c#c' are incident to the line o.

One of the most important logical features of planar projective geometry is connected to the duality relation. Each of the dual statements for the postulates for planar projective geometry is a theorem of this geometry.

For example:
Postulate: Given two distinct points there is a line with those points on it.
Dual Statement and Theorem: Given two distinct lines there is a point with those lines on it.

As a consequence of this feature, plane projective has a special result which is about the theorems of geometry and their dual statments.

The Principle of Plane Projective Duality:
Suppose S is a statement of plane projective geometry and S' is the planar dual statement for S. If S is a theorem of projective geometry, then S' is also a theorem of plane projective geometry.

The proof of this principle is a proof about proofs.
The idea is that a proof consists of a list of statements about lines and points.
Each statement in a proof is either one of the postulates, a previously proven theorem, or a logical consequence of previous statements.


So if we have a proof of a statement S, we have a sequences of statements A1,A2,...,AN=S.
Each of these statements is either one of the postulates, a previously proven theorem, or a logical consequence of proevious statements.


Now one can construct the sequence of dual statements A1', A2', ..., AN' = S'.
With a little argument it can be seen that each of these dual statements is also either a postulate, a theorem,or a logical consequence of previous statements.

Here is an application of the principle of duality to Desargues' Theorem. 

---


Desargues' Theorem: (in the (projective) plane). If two coplanar triangles (determined by points) ABC and A'B'C' are perspectively related by the center O, then the points of intersection X=(AB)#(A'B'); Y=(AC)#(A'C') ; and Z=(BC)#(B'C') all lie on the same line. 

---


Since Desargue's Theorem uses the hypothesis of a perspective relation between two triangles, we first look briefly at the dual concept.
Dual of Desargues' Theorem: . If two coplanar triangles (determined by lines) abc and a'b'c' are perspectively related by the line o, then the lines joining the points x=(a#b)*(a'#b')'; y=(a#c)*(a'#c') ; and z=(b#c)*(b'#c') all pass through the same point.

Note on Duality and the concept of perspective: We called two point triangles ABC and A'B'C' perspectively related with respect to a point O, if O is on the lines AA', BB' and CC'.
We define the dual concept  by saying that two line triangles abc and a'b'c' are perspectively related with respect to a line o, if o passes through the points a#a', b#b' and c#c'.

Notice that the Dual of Desargues' Theorem is also the logical converse of  Desargues' Theorem. Thus we can say, "The converse of Desargues' theorem is true by the duality principle."


---

• More on Conic Curves in Euclidean and projective geometries.



---

• Assignment:Watch the video "Conics" [VIDEO #628]. 
• Notice that from the ideas of projection from the vertex of the cone, any of the conic sections could be the shadow cast by the circle on a sectioning plane.



---

• Assignment: Watch FAPP on conics[ HSU Video #209- 3. Stand-up conic (Conic sections) (ca. 30 min.)]  and Video: Orthogonal Projection [HSU Video #4223] - connect this to central projections and conics.
• 
  
• Motivation: In the study of surfaces and solids in 3 dimension (as in the 3rd semester of calculus) one key method for undertanding a fugure in space is to consider a planar cross-section. This is a planar figure determined by the intersection of the spatial figure with a plane. Of course we have examined just this kind of section in our introduction to the conic sections!

We can consider this as well as what happens when a 3 dimensional object passes through Flatland.
Examples: A cube has cross sections that might be a point, a  line segment, a triangle, a square, a rectangle, a quadrilateral,  a pentagon, or a hexagon.
A tretrahedron has a cross section that might be a point, a  line segment, a triangle, a square, a rectangle, or a quadrilateral.
 
• In a plane we consider a figure to be made up of points and lines. A section of a planar figure, F, by a line l, where l is not in the figure F,  is a new figure consisting of the points P where P = l # m for any m, a line in the figure F.

Examples: The section of the triangle abc by the line l, is the set of three points on l , {a# l,b# l, c# l}.
The section by a line l (not passing through the point O) of a pencil of lines on the point O is the set of points on l with one point for each line in the pencil.

The dual concept for section: A section of a planar figure, F, by a point L, where L is not in the figure F,  is a new figure consisting of the lines p where p = L*M for any M, a  point in the figure F.
Examples: The section of the triangle ABC by the point L, is the set of three lines on L , {A*L,B*L, C*Ll}.
The section by a point L (not lying on a line o) of a pencil of points on the line o is the set of lines through L with one line for each point in the pencil. 

---


Point Perspective in the Plane: Figure F is perspectively related to Figure F' by the point O if there is a correspondence of the points of F with those of F' so that for any corresponding points, A in F and A' in F', the point O lies on the line A*A' .
Notes: 1. If the figure F and the figure F' are similar because of a central similarity, then F and F' are prespectively related.
2. If the figure F and the figure F' are congruent because of a translation, then F and F' are prespectively related by the point on the horizon line determined by the translation vector.
3. If the figure F and the figure F' are congruent because of a rotation by 180 degrees about the center O, then  F and F' are prespectively related by the point O.
 

Line Perspective in the Plane: Figure F is perspectively related to Figure F' by the line o if there is a correspondence of the line of F with those of F' so that for any corresponding lines, m in F and m' in F', the line o passes through the point m#m' .
Notes:1. If the corresponding lines in two figures F and F' are parallel, then in the affine plane, these corresponding lines will meet on the horizon line. Thus these figures are perspectively related in the projective plane.
2. If the figure F and the figure F' are congruent because of a reflection, then F and F' are prespectively related by the line of reflection.

---

A look at perspective of planar figures with respect to a center O and its dual: perspective of planar figures with respect to an axis o.

---

• Java Figures for Perspective
  

Sorry, this page requires a Java-compatible web browser.

•  Perspective relation as a transformation: Given O and point ABC on a line l, and a second line l',  we can determine unique points A'B'C' on l' by A' = OA#l',
  
B' =OB#l', and C' = OC#l'. Thus A'B'C' are perspectively related to ABC with center O.



• ---

• For Reading: A side trip to planar graphs and dual graphs. The term duality is used in many different mathematical contexts.In the study of planar graphs we can find an example of the use of "duality" that illustrates some of the aspects of mathematical duality. A planar graph consists of a finite set of points called vertices, line (straight or curved) segments with these vertices as endpoints called edges, enclosing planar sets called regions. We can think of these regions as geographic states, the edges as boundaries between land sections, and the vertices and places where these boundaries meet. So a planar graph G is a set of vertices, edges, and resulting regions in the plane.The dual graph of G is another graph, which for now we'll denote D(G). D(G) consists of a vertex for each region in G, a region for each vertex in G, and an edge for each edge. If R is a region in G, we choose a point in R, call it r, as a vertex of D(G). For each edge, E, of G, with regions R1 and R1 bordering on E, choose an edge, e, between r1 and r2 that crosses E. Finally, suppose V is a vertex of G. consider the edges that end at V and the regions that border these edges. Then these regions and edges correspond to vertices and edges of D(G) that surround a region which we'll denote v. The graph D(G) consists of the vertices, r, edges, e, and regions v just described. One aspect of the dual graph is that information about it is revealed by knowing information about the graph G. For example, if G has 5 regions, the D(G) has 5 vertices. If G has 7 edges then D(G) also has 7 edges, and if G has 4 vertices, then D(G) has 4 regions. The feature that duality exposes here in these statements is the replacement of the word "vertex" in the statement about G with the word "region" in the statement about D(G)  and the word "region" in the statement  about the graph G with the word "vertex" in the statement about D(G).


Duality and  Sections in Space.
 
• Duality in space: objects are points, lines, and planes.

Consider duality with spatial figures: the platonic polyhedra, tetrahedron, cube, octahedron,dodecahedron, icosahedron.
Point - plane duality... leaves line-line.
S: A point C and a line AB determine a plane (The join or span AB-C) .
S': A plane ABC and a line l  determine a point (the intersection ABC#l).
This duality is more like the graph duality  discussed earlier.
Notice that as figures, the cube and octahedron are dual, the octahedron and icosahedron are dual, and the tetrahedron is dual to itself.

Take a look at this: Encyclopedia of Polyhedra 

Here is a table showing the five platonic solids and the duality relation of Vertices, Edges (lines), and Faces (Planes):


The 5 Platonic Solids	V	F	E
Cube	8	6	12
Octahedron	6	8	12
Icosahedron	12	20	30
Dodecahedron	20	12	30
Tetrahedron	4	4	6

---


Sections in Space:
Section by a plane: Suppose F is a figure in space consisting of points, lines, and planes. Suppose p is a plane that is not containing any element of the figure F. Then the section of F by p is the figure with lines determined by the intersection of the planes  in F and p , the points detemined by the intersection of the lines in F with p  .
Example. The figure F is a tretrahedron. p is a plane that is distinct from the tretrahedron's elements. The section consists of 4 lines and the six points where those lines intersect in the plane of  p . [ Include Figure here.]

Section by a point: Suppose F is a figure in space consisting of points, lines, and planes. Suppose P is a point that is not contained in any element of the figure F. Then the section of F by P is the figure with lines determined by the join of the points  in F and  P , the planes detemined by the join of the lines in F with P.

Example. The figure F is a tetrahedron. P is a point that is distinct from the tetrahedron's elements. The section consists of 6 planes and the 4 lines where those lines join the vertices to the point P .

---

• Quadrangles and quadrilaterals in the projective plane.

A Triangle is a figure composed of  three points and three lines in the plane. A triangle is a planar self- dual figure. This is not so for a quadrangle and quadralateral. We look at the simple quadrangle and quadralateral, and the complete quadrangle and dual quadralateral, which has three diagonal points.
 
 

The Complete Quadrangle:  4 points {A,B,C,D} determine 6 lines {AB,AC,AD, BC, BD, CD}  and three additional points {X,Y,Z}.

The Complete Quadilateral:  4 lines {AB, BC, CD,AD}determine 6 points {A,B, C, D, X,Y}  with three additional lines{AC, BD, XY} .

 
Postulate: The three diagonal points in a complete quadrangle do not lie on the same line.
[This eliminates the 7 point geometry as a projective geometry with these axioms.]
Watch: Inversions [ HSU Video #4222]

---

Duality and graphs in the ordinary plane.

A basic principle is discussing graphs of equations and functions in the plane is the following:
Any point described by coordinates is intersection of two lines, any line is the join of two points.
Curves in the study of calculus are figures determined by points. For example the line with equation y= 2x+1 is a figure made up of points with coordinates of the form (a, 2a+1). Each of these points is determined by the intersection of two lines: X= a and Y = 2a+1.
We can dualize this figure to a figure made up of lines determined by the join of points (on two separate axes)  x=a and y = 2a+1. Notice that in the original line figure all the points lie on the same line, while in the dual figure all the lines will pass through a common point. Thus this second figure shows a perspective relation between the corresponding points on the  two axes. [Also the line in the graph of this function gives a perspective relation between the pencils of lines parallel to the X and Y axes!]


---


We can consider other function relations in this dual visualization as perspective relations (or perspective functions).
For example f(x) = x + 1 [or f(x) = x] are perspective between the parrallel axes determined by the appropriate point at infinity in the affine (projective) view.

Definition: The product (composition) of two or more perpectivities is a called a projectivity.
Is we compose two perspectivities we can transform points on a line to a second line and then back to the original line.
Thus the map from a euclidean, affine, or projective line to itself can be a projective transformation.

Example: Translation of a euclidean coordinate line by adding 1 unit.
T(P_x) = P_x+1 can be realized as a product of perspectivities in the affine plane.
First use the perspectivity that transforms the point P_x on the X axis to the point P' = Q_x+1 on the Y axis.
Then use the perpectivity that transforms the point Q_x+1 on the Y axis back to P_x+1 on the X axis.
Then if T represents the product of these two perspectivities, T(P_x) = P_x+1.

Other examples of projective line transformations include central reflection [Use P' =Q _-x  for reflection about 0]and central similarities [Use P' =Q _ax  for central similarity with scale a   and center 0]. 

---

Watched Video :Central perspectivities [ HSU Library 4206]

Curves are determined by lines.
Projective relation and projectivity between points on lines (and dual) and then points on a single line.
A little about conic curves and coicndences: A brief introduction to Pascal's Theorem/ Coincidence.

• The set of projectivities can be considered a group (as did isometries) , i.e. a set together with an operation which satisfies certain nice algebraic properties: closure, associativity, an identity and inverses.

• Projectivities and geometric transformations of a line.
• Isometries
• Similarities
• Inversions!

• Transformations with homogeneous coordinates of a line. Consider the isometry T of an ordinary (or affine) line with coordinates that translates a point 3 units to the right.  This isometry is indicated using the ordinary coordinates by T(Px) = Px+3 or T(x) = x + 3. If we wish to understand this isometry using the homogeneous coordinates of an ordinary point we recognize that Px = <x,1>.  So for an ordinary point, T(<x,1>) = <x+3,1>.

Notice that the ideal point will be left fixed  by this translation, that is, T(<1,0>) = < 1,0>. In fact the ideal point is the only fixed point of translation. We can see this also by looking at the visualization of the translation construction on an  affine line.

But what is the algebra for this isometry when using arbitrary homogeneous coordinates for an ordinary point?

T(<a,b>) = T(<a/b, 1>) = <a/b + 3,1> = <a+3b,b>.

In summary, T ( <a,b>) = <a+3b,b>.
Notice this formula works as well for the ideal point on the affine line.
This work can be done using some ideas from linear algebra. Recall that in matrix multiplication:

[	1	3	]	[	x	]	=	[	x+3	]
	0	1			1				1

and
 

[	1	3	]	[	a	]	=	[	a+3b	]
	0	1			b				b

So the isometry of translation can be considered from the point of view of algebra with homogeneous coordinates:
Treat the coordinates as a column vector, multiply by a square matrix, and then using the components of the resulting column vector as the homogenous coordinates for the transformed point. 

---



More on line transformations with homogeneous coordinates .
These transformations can be identified with matrix multiplications since A(cv)=cAv for A a matrix, c a scalar, and v a column vector so that pairs of homogeneous coordinates for one point are transformed to homogeneous coordinates for a single point.
Translation: T(x)=x+3 became

[	1	3	]	[	a	]	=	[	a+3b	]
	0	1			b				b

---

Reflection R(x)= -x  uses the matrix
 

[	-1	0	]
	0	1

 Thus

[	-1	0	]	[	x	]	=	[	-x	]
	0	1			1				1

and

[	-1	0	]	[	a	]	=	[	-a	]
	0	1			b				b

---

Dilation by a factor of 5  M(x)=5x  uses the matrix
 

[	5	0	]
	0	1

 Thus

[	5	0	]	[	x	]	=	[	5x	]
	0	1			1				1

and

[	5	0	]	[	a	]	=	[	5a	]
	0	1			b				b

---

Inversion I(x)=1/x uses the matrix
 

[	0	1	]
	1	0

 Thus

[	0	1	]	[	x	]	=	[	1	]
	1	0			1				x

and

[	0	1	]	[	a	]	=	[	b	]
	1	0			b				a

---

Notice that composition of these matrix transformations corresponds to matrix multiplication.


---

Definition: A general projective transformation of a projective line is a transformation that can be expressed using homogeneous coordinates for the points on the line and an invertible 2x2 square matrix.

If we let the matrix of these transformation be denoted by

T= [	a	b	]
	c	d

  Because T is an invertible matrix, the determinant of T= ad-bc is not zero, and conversely if the determinant of T= ad-bc is not zero, then the matrix T defines a projective transformation.

[	a	b	]	[	x	]	=	[	ax+b	]
	c	d			1				cx+d

and

[	a	b	]	[	x	]	=	[	ax+by	]
	c	d			y				cx+dy

 Thus x' = ax+by and y' = cx+dy.

---


We have shown now that all the transformations of the line we had previously discussed in the course were examples of this general type of projective transformation. 

---


Notice that the transformation defined by the matrix T
does not depend on which of the homogeneous coordinates are used to represent a point, since

[	a	b	]	[	kx	]	=	k[	ax+by	].
	c	d			ky				cx+dy

 Furthermore the matrix kT defines the same transformation as T for a similar reason since

k[	a	b	]	[	x	]	=	k[	ax+by	].
	c	d			y				cx+dy

 Noticing again that ad-bc is not zero, at least one of the entries, say a, in the matrix is not zero.  Using k  = 1/a we can assume that the matrix has the form

T= [	1	b	].
	c	d

---

Focus Question: Which transformations leave the point at infinity fixed?
Analysis: Using homogeneous coordinates for the point at infinity, it can be expressed as <1,0>.
The question is: For what matrices will this point be transformed to a point with homogenous coordinates of the form <?, 0> where ? is not zero?
For this to be true, we can see from the matrix equation

[	1	b	]	[	1	]	=	[	x	]
	c	d			0				0

that c = 0. Thus the transformations that leave the point at infinity fixed are of the form,
 

T= [	1	b	].
	0	d

Then recognizing that the determinant of T is not 0, it follows that d is also not 0.
Thus these transformations are of the form on a finite point:
:

[	1	b	]	[	x	]	=	[	x/d+b/d	]
	0	d			1				1

and

[	1	b	]	[	x	]	=	[	x+by	]
	0	d			y				dy

 Thus this transformation involves a translation if b is not 0, and a similarity of d  is not 0.


---

Reminder: Next Quiz #3 on TBA - Sample will be available over weekend.

---




An overview of what we've considered so far-

Euclidean Geometry  lines/planes	Affine geometry  lines/planes	Finite geometry  lines[/Planes?]	Projective Geometry  lines/planes
Axioms      Euclid      Hilbert	No Axioms  Yet  A figure indicating  an ideal point or line	Axioms  7 points/7lines  A figure.	M & I Axioms  A figure indicating  all points and lines
Parallel lines don't meet	Parallel lines meet  at an ideal point.	All pairs of lines  have a common point	All pairs of lines  have a common point
Coordinates       Analytic/Algebraic	Ordinary coord's  w/ infinite (ideal) points  Homogeneous Coordinates	Homogeneous Coordinates  with coefficients in {0,1}= Z 2	Homogeneous Coordinates  with real number coefficients
Transformations      Isometries      Similarities	Similarities	?	perspective and projective transformations.

---


 
• Consider the construction of P1/2 from P0, P1 and P¥ on the projective line. This begins a discussion of a harmonic relation between four points on a line. We observed that in fact the relation was present between P0, P1, P¥ and P1/2.

  ---

Harmonic Relation of 4 points on a line. [This will be the chief tool used to introduce (homogeneous) coordinates into projective geometry.] Four points on a line l are harmonically related if the line is determined by a pair of points from the intersection of lines in a complete quadrangle and the intersection of that line with the other two sides of the complete quandrangle. [In the figure: The line XZ would determined two other points, XZ#AD=R and XZ#BC=S, so that the points XRZS are harmonically related.] This would be denoted H(XZ,RS). Four points on a line that are  harmonically related: Using the text notation we can show that  if H(AB,CD) then H(BA,CD), and also conversely if H(BA,CD) then H(AB,CD). This is the meaning of saying "H(AB,CD) is equivalent to H(BA,CD)". Similarly we can show H(AB,CD) equiv. to H(AB,DC) and H(BA,DC). One way to see this is to envision relabeling the original quadrangle to reverse the order in which the points on the line are organized. Java Figures for harmonics (work in progress). Sorry, this page requires a Java-compatible web browser.  Notice the relation between the "double points" in the figure and the "single points". Proposition: H(RT,SU) is equivalent to H(SU,RT)  I.e., if H(RT,SU) then H(SU,RT). Link to the proof (adapted from Meserve & Izzo). Sorry, this page requires a Java-compatible web browser.

---




• ---

  
  
• Recall the construction on the affine line of the point P1/2 from P0,P1, and Pinf.


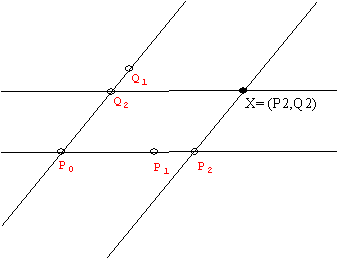
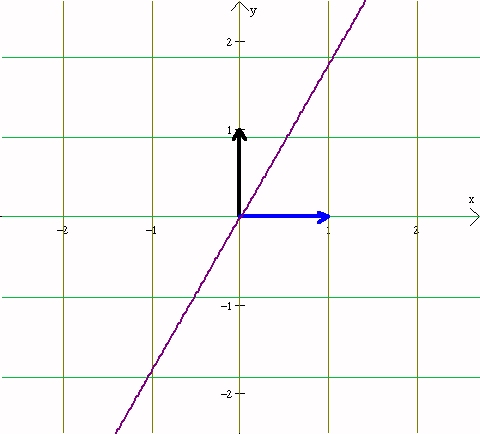
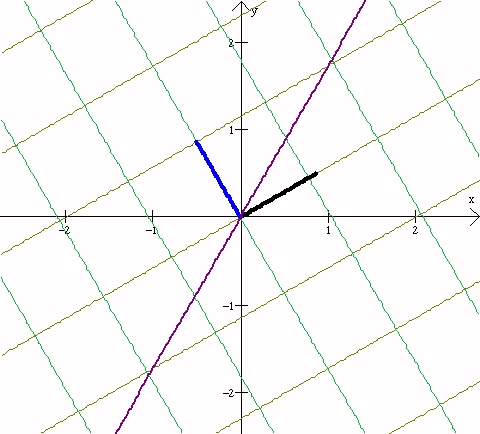
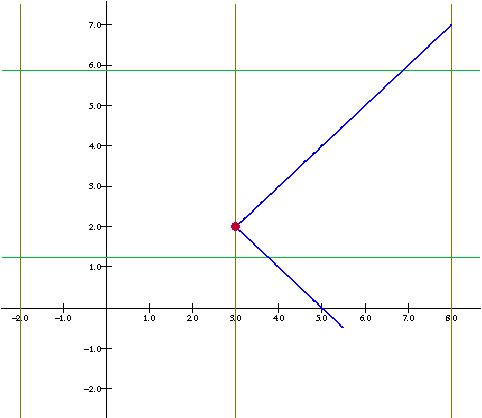
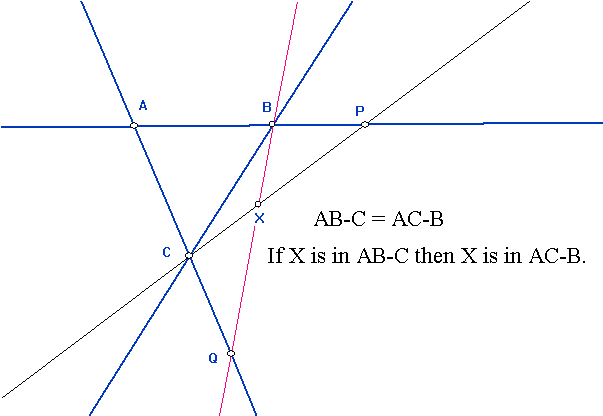
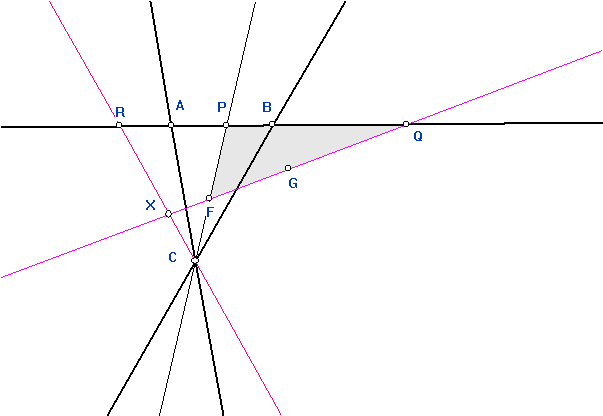
Notice that the figure used to construct P1/2 showed that H(P0 P1,  Pinf, 1/2).
Notice that the construction on the affine line of the point P2 from P0,P1, and Pinf looks the same.

Notice that the figure used to construct P2 shows that H(P1 Pinf, P0 P2).
In general, following this  construction of P2, it is possible to construct a fourth point, D, on a line given A,B and C already on the line so that H(AB,CD). We can use the construction of P2 to show how to construct the point D in general. This will be the key to giving a correspondence between points on a projective line and the real numbers with ¥ as a single additional "number" added to extend the set of numbers.

One key issue then is:
Is the point constructed from the points A, B and C uniquely determined by the fact that it is in the harmonic relation with A, B, and C? That is, if A,B, and C are three points on a line and D and D* are points where H(AB,CD) and H(AB,CD*), then must D=D*?
This is the question of the uniqueness of the point D. We can prove that in fact the point D is uniquely determined.

---

---

 The proof follows the argument of Meserve and Izzo.
It used Desargues' theorem several times.

Discussion of the dual concept of a harmonic relation between four lines passing through a single point.
Theorem: If A,B,C, and D are on a line l  with H(A,B,C,D) and O is a point making a section with these four points, consisting of the four lines a,b,c and d, then H(a,b,c,d).
Proof: see M&I Theorem 5.4.
Corollary: (By Duality)  If a,b,c, and d are on a point O  with H(a,b,c,d) and l is a line making a section with these four lines, consisting of the four points A,B,C and D, then H(A,B,C,D).

Application:
We can think of a perspectivity between points ABCD on line l and A'B'C'D'  on the line l' with respect to the point O as being a section of the points ABCD by the point O followed by a section by the line l' of the lines a,b,c, and d on the point O.
Applying the previous theorem and its corollary we see that: If H(AB,CD) then H(ab,cd) and thus H(A'B',C'D').

Note: This application shows that if four harmonically related points on a line are perspectively related to four points on a second line, then the second set of four points is also harmonically related. Furthemore, this result can be extended easily to points that are projectively related.
Thus the transformations of projectivity in projective geometry preserves the harmonic relationship between four points.

[This last note is comparable to the fact that in Euclidean geometry, isometries preserve length, and in affine geometry that similarities preserve proportions.]


---



Harmonic Conjugate as a Transformation: Given A,B, and C points on a projective line, we have shown that there is a unique point D so that H(AB,CD). D is called the harmonic conjugate of C with respect to AB.

In many ways this gives a transformation of the point on the line to other points that is similar in its nature to reflections and inversions. Notice that on a projective (affine) line two point will cut the line into two disjoint pieces, as does a single point for reflection and the points P_R and P_-R for inversion, where the transformation maps points in one set into the other while leaving the "boundary points" fixed.


---

With the existence and uniqueness of the point D established, we can now consider some examples illustrating how to establish a coordinate system for a projective line by choosing three distinct points to be P0, P1, and P¥.
We can construct P2, P-1, P1/2,  (in two different ways).
Exercise: Construction  P3 and P1/3.
Show that  with the choice of three points on a projective line we can construct points using harmonics to correspond to all real numbers (as in our informal treatment of the affine line).

---



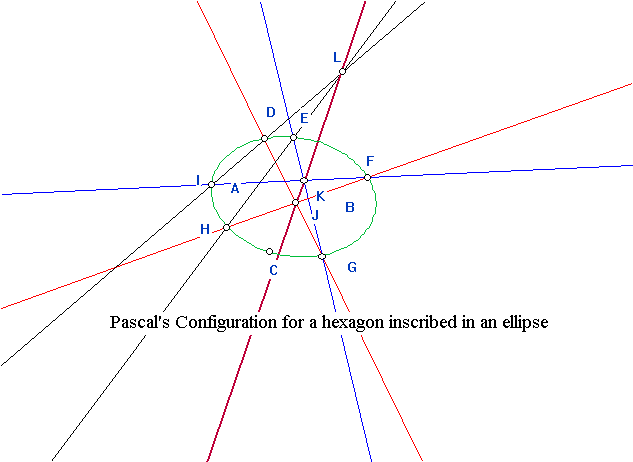
Conics revisited: Pascal and Brianchon Theorems:
Point and line conics.
Consider lines connecting  corresponding points in a pencil of points on a line related by a projectivity (not a perspectivity) and noticed that the envelope of these lines seemed to be a conic, a line conic. Notice briefly  the dual figure which would form a more traditional point conic. [Also notice  how line figures might be related to solving differential equations e.g. dy/dx=2x-1 with y(0)=3 has a solution curve determined by the tangent lines determined by the derivative: y=x^2-x+3 which is a parabola.]
Watch video on conics.  Projective generation of conics HSU VIDEO2574

---
Proof of Brianchon's Theorem.
Duality for Pascal's Theorem.
Use of Pascal's Theorem to construct a conic from 5 points.





---

 
A brief excursion back to the Inversion Transformation.

---
Projective transformations of the plane and computers graphics.

The complex numbers, C, and the geometry of CP(1).
The ordinary points on this "line" can be visualized as a plane or all the points of a sphere except one- which corresponds to the north pole or the point at infinity. [Compare this to the visualization of RP(1) as a circle.]
Algebraic projective transformations of CP(1).
This means first examine what it means for these to be affine, and then the geometry of addition and multiplication of complex numbers.
Addition of a constant complex number corresponds to a translation.
Multiplication by a constant corresponded to a dilation using the absolute value of the complex number for the factor and a rotation by the angle the corresponding vector mad with the positive real axis.
An affine transformation can preserve the distance between complex numbers  if |a|=1 where a is a complex number, so a can be thought of a point on the unit circle and multiplication by a corresponds to a rotation. So affine transformations of CP(1) are rotations followed by translations of the plane of complex numbers.
What about inversions... ?


---

Review of algebraic projective transformations of the real projective line RP(1).

RP(1) is characterized using the homogeneous coordinates as a set of pairs of real numbers <a,b>, not both zero, with <a,b>=<c,d> in the case there is a nonzero real number t so that c=ta and d=td.
The transformations correspond to 2x2 matrices with non-zero determinant. These form a group under composition (matrix multiplication) and we have looked at many examples to see how a matrix transforms points on the projective line with coordinates to other points on the projective line.

We will see how this transformation is completely determined by the correspondence of three distinct pairs of points. In some cases the transformation  transforms an ordinary point to an ordinary point, the ideal point to an ordinary point and an ordinary point to the ideal point, and in some cases the transformation will transform the ideal point to the ideal point.

A transformation that transforms the ideal point to the ideal point is called an affine transformation. The composition of two affine transformations is an affine transformation. The inverse of an affine transformation is an affine transformation and clearly the identity transformation is an affine transformation, so the affine transformations are also a group under the operation of composition (matrix multiplication).
 

Projective transformations of  RP(2) with examples of transformations previously discussed in the course.
Using homogeneous coordinates of points in the affine plane, we consider these as points in RP(2). Consider the isometries of translation, rotation, and reflection of the plane, extended to the affine plane and thus to RP(2).

Translation by <a,b>:
Rotation at (0,0) = <0,0,1>
Reflection about the X- axis:
Reflection about the line Y=X:

Central Similarities at (0,0) by a factor of M.

Reconstruction of a point on a conic from Pascal's Theorem.

The following materials are from previous course notes and have not been incorporated into the current course notes.

Consider lines connecting  corresponding points in a pencil of points on a line related by a projectivity (not a perspectivity) and noticed that the envelope of these lines seemed to be a conic, a line conic. Notice briefly  the dual figure which would form a more traditional point conic. [Also notice  how line figures might be related to solving differential equations e.g. dy/dx=2x-1 with y(0)=3 has a solution curve determined by the tangent lines determined by the derivative: y=x^2-x+3 which is a parabola.]
 
 

In discussing the issue of whether the 5th axiom could be proven from the other four axioms, we looked at an example of another axiom system, with an axiom N (any pair of lines having at one point in common) and an axiom P (given a line l and a point P not on that line there is a line m where P is on m and m and l have no common points) which is a version of the parallel postulate (Playfair's - not Euclid's). We gave examples showing that the four axioms and P were possible as well as the four axioms and N were possible. This showed that one can not prove axiom P or N from the other four axioms since P and N are contradictory.

By a similar analysis of the axioms for the seven point geometry we showed that it not possible prove the 5th postulate from the other four. The analysis examines the example of the seven point geometry and notices that by including an 8th and 9th point the resulting geometry would satisfy the other 4 axioms.

The model we have for affine geometry still satisfies the parallel postulate, since the ideal (infinite) points of affine geometry are not considered as ordinary points of the geometry. However, be removing this distinction between ordinary and ideal points and considering the geometry that results we obtain a geometry in which there are no parallel lines. (A projective plane.) This will be a major focus of discussion for the remainder of the term- especially using the homogeneous coordinates to consider points in this geometry from an analytic/algebraic approach.
 

Initial discussion considered the problems of perception and how the position of an object in a picture can affect our judgment on its relative size. Turning directly to the question of perspective in drawing we looked at how an artist tries to capture the visual reality of perception by drawing figures larger when they are closer to the eye of the beholder. We looked at some Durer drawings showing some mechanical ways to draw accurate perspective figures.

 

 

An examination of the problems of transferring an spatial image of a plane to a second plane using the idea of lines of sight we arrived at an understanding of how points in the plane would correspond to lines through a point (the eye).

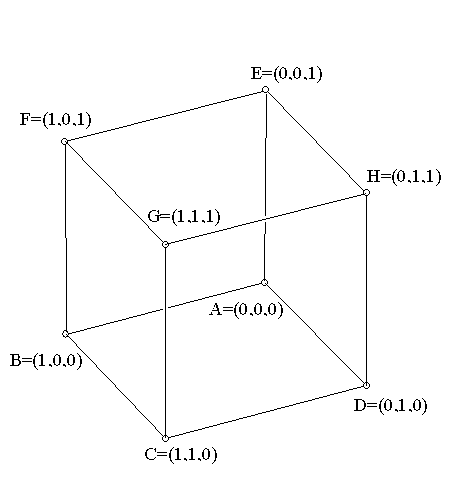
In discussing the 7 point geometry we visualized it using vertices of a cube (besides (0,0,0)) with their ordinary coordinates in standard 3 dimensional coordinate geometry and identified the 7 points . This allowed us to identify "lines" using the homogeneous coordinate concepts and their relation to planes in three dimension through (0,0,0). We identified all but one of the lines easily- the last plane has ordinary equation X + Y + Z = 2... but in this arithmetic for {0,1} we have 1+1=0, so 2=0 and the vertices of that satisfy this equation in ordinary coordinates {(1,1,0), (1,0,1),(0,1,1)} form a line as well.

We then discussed using {0,1,2} for homogeneous coordinates connected to the arithmetic given by the tables
 


 




+	0	1	2		*	0	1	2
0	0	1	2		0	0	0	0
1	1	2	0		1	0	1	2
2	2	0	1		2	0	2	1

The homogeneous coordinates for this set identify ordered triples, for example: <1,0,1>=<2,0,2> and <1,0,2>=<2,0,1>.  There are 27 possible ordered triples, and thus 26 when we exclude (0,0,0), and these are each paired by the factor 2 with another triple, so there will be exactly 13 points ( and by the comparable work with lines) and 13 lines in this geometry.
.... some details still to be reported.
 
 
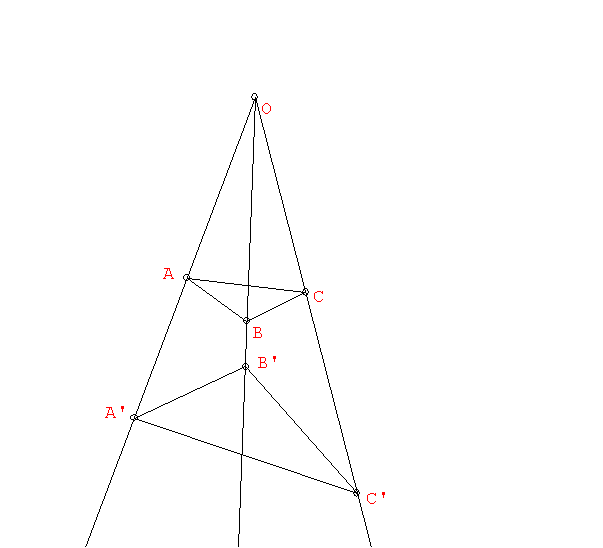
We  watched the film on central perspectivities that discussed perspectivities and projectivities in the plane. Any perspectivity between a pencil of points on one line and that one another line can be thought of as a transformation. This transformation is completely determined by the relation of two pairs of distinct points on two lines. For a projectivity (the composition of a finite number of perspectivities) the result is that a projectivity is completely determined by the correspondence of three points. This result is called the fundamental theorem of projective geometry and is taken as an axiom by M&I.

 

 
 
 
 
 

[Moved from earlier: The lab time was spent working on sketches showing ways to understand that result of the CAROMS film about the inscribed triangles of minimum perimeter.In Lab: Discuss some visual features such as trace and animation and start to look at the use of coordinates. We'll do more with coordinates, along with the use of traces and locus to see some aspects of coordinate geometry next week.]

We also watched the film on projective generation of conics which introduced Pascal's theorem and its converse about hexagons inscribed in a conic and showed how to use this result to construct a conic curve passing through any 5 points. This work was also related to projectivities between pencils of lines. We will be considering this further in the course. After a short break we continued using metric ideas to construct an ellipse  as a locus on sketchpad and discussed how to do a parabola as well. By next Thursday students should construct examples of the three conics on sketchpad using metric ideas.
 

Okay... just a quick recall of some of what we covered:
1. Now that we've established how to connect homogeneous coordinates to a projective line using harmonics we continued by looking at some more algebraic projective lines- with coefficients of Z₂, Z₃, and Z₅, we saw that these projective lines would have 3,4, and 6 points respectively, corresponding to the 2,3,and 5 ordinary points and one ideal point. This lead to
2. A discussion of using the complex numbers, C, and the geometry of CP(1). The ordinary points on this "line" can be visualized as a plane or all the points of a sphere except one- which corresponds to the north pole or the point at infinity. [This was compared to the visualization of RP(1) as a circle.]
3. The discussion turned to algebraic projective transformations of RP(1). When these leave the ideal point fixed they are called affine transformations and form a group under composition. We showed that an affine transformation has a matrix of the form

a	b
0	1

and therefore T(Px)=Pax+b. Thus an affine transformation of the projective line is a dilation/reflection followed by a translation.
4. We looked at the idea of establishing the idea of a distance between ordinary points using absolute value-

d( <a,b>,<c,d>) = |a/b - c/d|.    We showed this is well defined and then discussed what the isometries for this distance would be. After some analysis we saw that this would mean that in the matrix of an isometry |a|=1, so a=1 or a=-1. I.e,  the matrix is

+/-1	b
0	1

or that T(Px)=P+/-x+b. Thus an isometry of RP(1) is a reflection followed by a translation.
5. We also looked further at Pascal's theorem and its planar dual Brianchon's theorem. Next class we'll prove Brianchon's theorem using an elliptic hyperbaloid.
 Today we did more on algebraic projective transformations of CP(1). This meant first examining what it meant for these to be affine, and then the geometry of addition and multiplication of complex numbers. Addition of a constant complex number corresponded to a translation. Multiplication by a constant corresponded to a dilation using the absolute value of the complex number for the factor and a rotation by the angle the corresponding vector mad with the positive real axis. We also saw how affine transformations could preserve the distance between complex numbers  if |a|=1 where a is a complex number, so a can be thought of a point on the unit circle and multiplication by a corresponds to a rotation. So affine transformations of CP(1) are rotations followed by translations of the plane of complex numbers. Notice these are all orientation preserving transformations. so any reflection of the plane is not an isometry in this geometry. We looked briefly at another transformation that was a reflection, namely complex conjugacy, T(a+bi)=a-bi. This is not an isometry in this geometry because it is orientation reversing.

 

 
 
 

We spent the remainder of the lecture time going over the proof of Brianchon's Theorem using the proof of Hilbert and Cohn-Vossen based on hexagons lying on the surface of an elliptic hyperbaloid (which is a ruled surface).