Triangulations
Theorem: Any polygon
can
be decomposed into triangles.
Proof: The key idea of the proof goes by the method of
mathematical
induction. Let n = the number vertices = the number of sides in the
polygon.
The induction starts by considering n=3. Then we
assume
that we have justified the result for polygons with k vertices where
k<n
and justify the result for n based on this assumption. This allows us
to
use "induction" to prove the result for any value of n. Starting with
n=3,
we have the result is true for n= 4, and then n=5, and then n=6,....
and
we can continue to any specific value of n.
We begin with a more careful characterization
of the polygonal regions being considered.
The key idea of the proof goes
by induction on the number n = the number vertices = the number of
sides
in the polygon, as follows:
When n = 3 the result is trivial.
Suppose n> 3 and that for any polygon with k vertices/ sides, where
k<n, the polygon can be triangulated.
Now proceed to consider the vertices, v1, v2, ..., vn ordered
so that vi is adjacent to vi+1 and vn is adjacent to v1.
Take a ray from v1 and rotate it from v1v2 so that it intersects
the inside of the polygon. continue to rotate until it meets another
vertex.
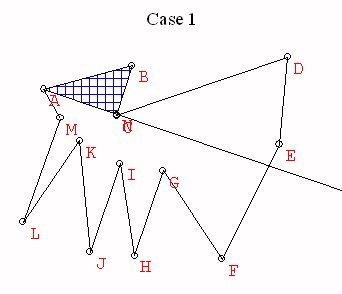
Case 1. This vertex is v3. Then consider the polygonal region Q1
= v1v3...vn which has n-1 vertices.
By induction Q1 can be triangulated,
so the original polygon is triangulated using the triangulation of Q1
and
the triangle v1v2v3.
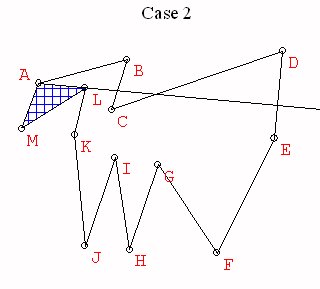
Case 2. The vertex is vn-1. Then consider the polygonal region Q2
= v1v2v3...vn-1 which has n-1 vertices.
By induction Q2 can be triangulated,
so the original polygon is triangulated using the triangulation of Q2
and
the triangle v1vnvn-1.
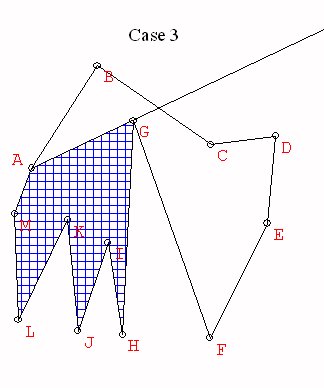
Case 3. The vertex is vk with k different
from 3 or n. Then consider
the polygonal regions Q3 = v1v2...vk which has k vertices (k<n) and
Q4 = v1vkvk+1...vn which has n-(k-2)<n vertices.
By induction Q3 and
Q4 can be triangulated, so the original polygon is triangulated using
the
triangulations of Q3 and Q4.
 End of Proof.
End of Proof.
For more discussion of proofs of this proposition see Triangulations
and
arrangements, Two lectures by Godfried Toussaint, transcribed by
Laura Anderson and Peter Yamamoto.



