To make this rectangular figure into torus, first imagine that the upper
and lower edges of this rectangle are bent toward each other until
they
touch.
Thomas L. Saaty - Paul C. Kainen: The Four-Color Problem.
Assaults and Conquest.
New York: Dover, 1986, p. 35.
Antreas P. Hatzipolakis <xpolakis@otenet.gr>
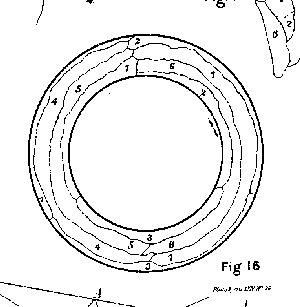
Another 7 color map on the torus may be found in Coxeter's
Introduction to Geometry, p. 387, Figure 21.3b. This is a nice
symmetric tessellation of the torus by seven hexagons, cut out
of the hexagon tessellation of the plane, and Coxeter attributes
it to Heawood.
Regards,
John Stillwell
Heawood's original paper, titled "Map-Colour Theorem," appeared in the
Quarterly Journal of Pure and Applied Mathematics, vol. 24 (1890),
pp.
332-338. The pertinent excerpt is reprinted in the book "Graph
Theory
1736-1936," by Biggs, Lloyd and Wilson (Oxford University Press, 1976),
pp. 112-115. There is an figure there of a torus map needing
7 colors.
I assume it's an exact reproduction of what's in the original paper.
Perhaps someone with access to the Quarterly Journal can confirm that.
My reason for assuming it's exact is that Biggs et al. also reprint
Kempe's 1879 "proof" of the 4-color theorem, which appeared in the
American Journal of Mathematics, and the figures there are identical
with those in a fascimile version of AJM available online through JSTOR
( http://www.jstor.org - but you need an institutional membership
to
do any searches). Again, perhaps someone with access to the original
can confirm that JSTOR's version is exact. (I'm pretty sure it
is. I
think what you see at JSTOR are scanned versions of the actual journals.)
In his 1879 paper, Kempe describes (in words) a map on a torus that
requires 6 colors. Presumably Heawood was the first person to
find one
that needs 7.
Barry Cipra
cipra@microassist.com
Heawood's original paper, titled "Map-Colour Theorem," appeared in the
Quarterly Journal of Pure and Applied Mathematics, vol. 24 (1890),
pp.
332-338. The pertinent excerpt is reprinted in the book "Graph
Theory
1736-1936," by Biggs, Lloyd and Wilson (Oxford University Press, 1976),
pp. 112-115. There is an figure there of a torus map needing
7 colors.
In case anyone simply wants a glimpse of the figure and the reference
to it
on p. 334 of Heawood's paper, I have scanned and placed them here:
http://www.lsus.edu/sc/math/rmabry/temp/heawood.htm
Rick Mabry

