There are two ways that we can generalize the example of Taylor's
theory for `e^x`.
(1) Use a function other than `e^x`.We'll begin our generalization by considering functions that are sufficiently nice when examined close to `0`. Here's a definition that makes more precise what we mean by "nice."
(2) Investigate the function at a point `x=a` different from `0`.
Definition IX.B.1: A function `f ` is called `C^{oo}` ("C- infinity") on an open interval if for every natural number `n`, `f^{(n)}(x)` exists for each `x` in the interval, i.e.,`f ` has derivatives of order `1,2,3,4,...` on the interval.
ASSUMPTION: FOR THE REMAINDER OF THIS SECTION, ASSUME THAT `f
`
IS A `C^{oo}`
FUNCTION ON AN OPEN INTERVAL I THAT CONTAINS 0.
Proposition IX.B.2: Let `P_n(x) = f(0)+f'(0)x + {f''(0)}/2
x^2
+{f'''(0)}/{3!} x^3+...+{f^{(n)}(0)}/{n!} x^n`.
Then
`P_n(0)=f(0), P_n'(0)=f'(0), P_n''(0)=f''(0)` ,... , and
`P_n^{(n)}(0)=f^{(n)}(0)`.
Proof:. `P_n'(x) = f '(0)+f ''(0)x + { f '''(0)}/2 x^2 + ...+{f^{(n)}(0)}/{(n-1)!} x^(n-1)`. So `P_n'(0)=f '(0)`.
The other equations are demonstrated similarly. EOP.
Definition: Let `P_n(x,f) ` denote the polynomial of the
last
proposition, so
`P_n(x,f) ` is called the Maclaurin's Polynomial of degree n for `f`.
Remark: With this notation we have shown in the proof above that the derivative of the Maclaurin's Polynomial of degree `n` for`f` is the Maclaurin's Polynomial of degree `n-1` for the derivative of `f`, that is,`P_n'(x,f)= P_{n-1}(x,f')`.
Futhermore, since `P_n^{(n)}(x,f)=f^{(n)}(0), P_n^{(n+1)}(x,f)=0` for all x. Thus `P_n(x,f)` actually solves the differential equation `g^{(n+1)}(x)=0` with initial conditions `g(0) = f(0), g'(0) = f '(0), g''(0)=f''(0)`, ... , and `g^{(n)}(0)=f^{(n)}(0)`.
Example IX.B.1: Find the Maclaurin's polynomial of degree 4 for `f(x)=e^{3x}`.
Solution: This is a matter of some systematic use of the
calculus
of derivatives.
`f(x)=e^{3x}` so `f(0)=1`.
`f'(x) = 3e^{3x}` so `f '(0) = 3`.
`f''(x)= 9e^{3x}` so `f ''(0) = 9`.
`f '''(x)=27e^{3x}` so `f '''(0) = 27`.
`f^{(iv)}(x) = 81e^{3x}` so `f^{ (iv)}(0) = 81`.
Here is a table that can help organize
the work.
| `n` | `f ^{(n)} (x)` | `f ^{(n)}(0)` |
| `1` | `3e^{3x}` | `3` |
| `2` | `9e^{3x}` | `9` |
| `3` | `27e^{3x}` | `27` |
| `4` | `81e^{3x}` | `81` |
Therefore `P_n(x,e^{3x}) = 1+3x + 9/2 x^2 +27/6 x^3+81/24 x^4
=
1 +3x+9/2x^2+9/2x^3+27/8x^4`.
Proposition IX.B.3: (Corollary) If `f ` is a
polynomial
function of degree `m` on an open interval I that contains `0`
with
`f(x) = a_0 + a_1x+a_2x^2 + ... +a_kx^k+ ... +a_mx^m` then
for `0<= n<=m, P_n(x,f) = a_0 + a_1x+a_2x^2 +
... +a_kx^k+
... +a_nx^n` and in particular `f(x) = P_m(x,f)`
for any `x` in I.
Comment: This result
merely
notes that the Maclaurin Polynomial of degree `n` for a poynomial
`f`
corresponds to the sum of the terms of `f` of degree less than or
equal
to `n`.
Proof Outline: For the details of the proof here apply the result of Proposition IX.B.2.
| `n` | `f ^{(n)} (x)` | `f ^{(n)}(0)` |
| `0` |
`(1-x)^{-1}` | `1` |
| `1` | `(1-x)^{-2}` | `1` |
| `2` | `2(1-x)^{-3}` | `2` |
| `3` | `6(1-x)^{-4}` | `6` |
| `4` | `24(1-x)^{-5} | `24` |
Theorem IX.B.1: If `f` is a `C^{oo}`
function on an open interval I that contains `0` then `f(b)` is
approximately `P_n(b,f)`
for any `b` in I, and if
`R_n(b)=f(b)-P_n(b,f)`
then for some `c` between `0` and `b`, `R_n(b)=
{f^{(n+1)}(c)}/{(n+1)!}
b^{(n+1)}`.
Remark: You should check for yourself that when `f(x) = e^x`, this is merely a restatement of Proposition IX.A.1 .
Proof: Let `g(t) = f(t)+f'(t)(b-t) + {f''(t)}/2 (b-t)^2+...+{f^{(n)}(t)}/{n!}(b-t)^n + {R_n(b)}/{b^{(n+1)}}(b-t)^{(n+1)}` where we assume `b` is not `0` and `t` is in the interval I.
Then `g(0)=P_n(b,f) + R_n(b)= f(b)` and `g(b)= f(b)` as well. Thus, [using the Mean Value Theorem or Rolle's Theorem] for some `c` between `0` and `b` we have `g'(c) = 0`. But, after extensive use of the product rule, we find that
`g'(t)=f'(t) +
[f'(t)(-1)+f''(t)(b-t)]+[f''(t)(b-t)(-1)+{f'''(t)}/2
(b-t)^2]+...`
`+[{f^{(n)}(t)}/{n!}n(b-t)^{(n-1)}(-1)
+{f^{(n+1)}(t)}/{n!}(b-t)^{n}]
+{R_n(b)}/{b^{n+1}}(n+1)(b-t)^{n}(-1)`
so `g'(t)={f^{(n+1)}(t)}/{n!}(b-t)^{n}-{R_n(b)}/{b^{n+1}}(n+1)(b-t)^{n}`.
Now using `t = c` and `g'(c) = 0` we can conclude that
`{f^{(n+1)}(c)}/{n!}(b-c)^{n}={R_n(b)}/{b^{n+1}}(n+1)(b-c)^{n}` or
`R_n(b)={f^{(n+1)}(c)}/{(n+1)!}b^{(n+1)`.
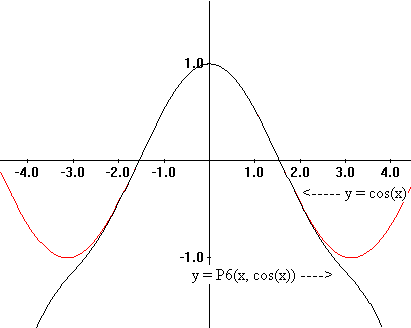
Example IX.B.2: Find `P_6(x,cos(x))`. Use
this polynomial to estimate `cos(1)`.

Solution: Let `f(x) = cos(x)`. Then it is
easy to verify that
`f(0) = 1`, `f '(0) = 0`, `f ''(0)= -1`, `f
'''(0)=0`, `f ^{iv}(0) =1`, `f ^v(0) = 0`, and
`f^{vi}(0)
=-1`.
Thus `P_6(x,cos(x))=1 - {x^2}/2 + {x^4}/24 - {x^6}/720`.
The following graph visualizes both the cosine function and the
polynomial
`P_6(x,cos(x))`. Notice how close these graphs are
when `x` is close to `0`.
We estimate `cos(1)` by evaluating `P_6(x,cos(x))`
when `x = 1`, so we find that
`cos(1)~~1 - 1/2+1/24 - 1/720 = {720-360+30-1}/720 = 389/720`.
Applying the remainder part of the theorem to this estimate
allows
us
to say that
`R_6(1) = {f^{vii}(c)}/{7!}1^7={sin(c))/5040` where `0 < c <
1`.
But since `0 < c < 1`, we have that `0 < sin(c)
< 1`, so that `0<R_6(1)<1/5040`.
In conclusion we have shown that `389/720 < cos(1)<389/720
+
1/5040`.
Here is a spreadsheet
showing
this computation and one using `n=14` as well.
Example IX.B.4: Find
`P_4(x,ln(1-x))`. Use
this polynomial to estimate `ln(0.9)`.
Solution: Let `f(x) = ln(1-x)`. This is a matter of some
systematic use of the
calculus
of derivatives.
`f(x)=ln(1-x)` so `f(0)=0`.
`f'(x) = -1/{1-x}=-(1-x)^{-1}` so `f '(0) = -1`.
`f''(x)= -(1-x)^{-2}` so `f ''(0) =- 1`.
`f '''(x)=-2(1-x)^{-3}` so `f '''(0) = -2`.
`f^{(iv)}(x) = -6(1-x)^{-4}` so `f^{ (iv)}(0) = -6`.
Here is a table that can help organize
the work.
| `n` | `f ^{(n)} (x)` | `f ^{(n)}(0)` |
| `1` | `-(1-x)^{-1}` | `-1` |
| `2` | `-(1-x)^{-2}` | `-1` |
| `3` | `-2(1-x)^{-3}` | `-2` |
| `4` | `-6(1-x)^{-4}` | `-6` |
Exercises IX.B: (Solutions 1-7 odd)
In exercises 1-10 , find `P_n(x,f(x))` for the specified function and `n`.
13 - 22. Using the polynomials found in problems 1-10, estimate
the
value of `f(1)` and discuss the related error term `R_n`.
23. Estimate `int_0^1 sin(t^2) dt`
using `P_5(x,sin(x))`. Discuss the error in this
approximation.
[Hint: Review the work done in the last section for `int_o^1
e^{-t^2}dt`.]