Motivation: In our models for learning we tried using several different functions for the learning rate, all of which were positive decreasing functions. We were fortunate in those examples to find indefinite integrals for many of those models. Here's one more example for which we will find a method of solution in this section.

What is L(2) and what is the limit of L(t) as t`-> oo`?

Note first from the product rule that `L''(t)= e ^{-t} - t e^{ -t} = e^{ -t} (1 - t)` so L''(t) < 0 for t > 1 and L'(t) is a positive decreasing function for t > 1. Just the kind of situation we've been analyzing. But we need a method for integrating this function. That is just what we'll develop in this section.

There are very few techniques for the calculus of indefinite integrals that arise on their own as features of integration. Besides use of the Fundamental Theorem of Calculus, it is primarily the reversal of the derivative calculus that leads to results about the indefinite integral. As an example of this notion recall that the technique called substitution (or change of variables) was in fact a restatement of the chain rule. In this section we investigate the technique of integration that results from reversing the product rule. This technique is generally described as integration by parts.

We begin with a simple example of the product rule to see how it can be reversed to give a result about indefinite integrals.

EXAMPLE VII.C.2 The derivative of  `f(x) = x cdot sin(x)` is found using the product rule, `f '(x) = x cos(x) + sin(x)`. We can translate this result easily into a statement about indefinite integrals by writing  `int x cos(x) +sin(x) dx = x sin(x)` and, using linearity, this means that

Now this gives us a result that is in fact new (for us at least),

To check this result we would differentiate `x sin(x) + cos(x)`, requiring of course the product rule in the check.

Let's see what we can generalize from this last example.

Integration By Parts: Suppose `y = v cdot z` where v and z are both functions of x. Then by the product rule we have `(dy)/(dx) = v cdot (dz)/(dx) + z cdot (dv)/(dx)`. Translating this into an integration relation we have

So....( you fill in the missing steps)

At this stage the notation of differentials is handy to give a slightly more compact version of this formula using `dz = (dz)/(dx) dx` and `dv = (dv)/(dx) dx` , namely:

Example VII.C.2 (revisited). In this example v = x and z = sin(x), so dv = 1 dx and dz = cos(x)dx and the last formula gives us directly

Example VII.C.3. Using the formula just derived, find `int x cdot e^x dx`.

Solution: We let v = x and `dz = e^x dx`, so that `z = e^x` and `dv = dx`. We obtain the result that

Again, to check this result by differentiation you will need to use the product rule.

Remarks: The use of integration by parts sometimes requires a clever choice for the parts. In the last example there were two other possible choices that would not have done as well:

i. Let `v = e^x` and `dz = x dx` would lead to `dv = e^ x dx` and `z = (x^ 2)/2`  so after applying the formula for parts we would need to find `int (x^2)/2 dx` which certainly looks worse than the original integral.

ii. Let `v = x e^x` and `dz = dx` would lead to `dv = e^x + x e^ x dx` and `z = x` so after applying the formula for parts we have

which also looks worse than the original integral since now the integrand involves `x^2` instead of `x`.

As a general principle the resulting integral after an application of the method of parts should not be worse in form then the initial integrand.

Sometimes the expression does not appear to have two factors to use for the parts. The next example illustrates this situation.

Example VII.C.4. Solve the differential equation `f '(x) = ln(x)`.

Solution: Our problem is to find  `int ln(x) dx` and for this we'll use integration by parts.

We let  `v = ln(x)` and `dz = dx` , so `dv = 1/x dx` and `z = x` are the remaining parts for the problem.

Comment: It is common to try to use integration by parts when a mixture of transcendental and algebraic functions are factors of the integrand. The next two examples illustrate this as well as a few other features that sometimes appear in problems involving integration be parts.

Example VII.C.5. Find an antiderivative for `e^x sin(x)`.

Solution: Using parts we let `v = e^x` and `dz = sin(x) dx` so that `v = e^x` and `z = - cos(x)`.

Thus we have

This result is no worse than the original problem so we continue, using parts in this problem a second time.
Let `u = e^x` and `dw = cos(x) dx` so that `du = e^x` while `w = sin(x)`. Thus we have

`int e^x cos(x) dx =  e^x sin(x) -  int  e^x sin(x) dx` .

Again our new integrand is no worse than the original problem, in fact, the integral is the same! The algebra of our work in this example may be summarized as `I = -e^x cos(x) + e^x sin(x) - I`. We solve for I and find `I = int e^x sin(x) dx = 1/2 [e^x sin(x) - e^x cos(x) ] + C`.

[Notice we do not abuse the letters v and z by reusing them in the problem. Instead we chose two other letters, u and w, to continue with different parts.
Lesson: Avoid confusion. Try not to abuse your symbols by overuse!

Example VII.C.6. Find `int_0^pi x sin(x) dx`.

Solution: In this definite integral we use parts as well. Here we can do the evaluation of the definite integral as the parts evolve. In this fashion we find that

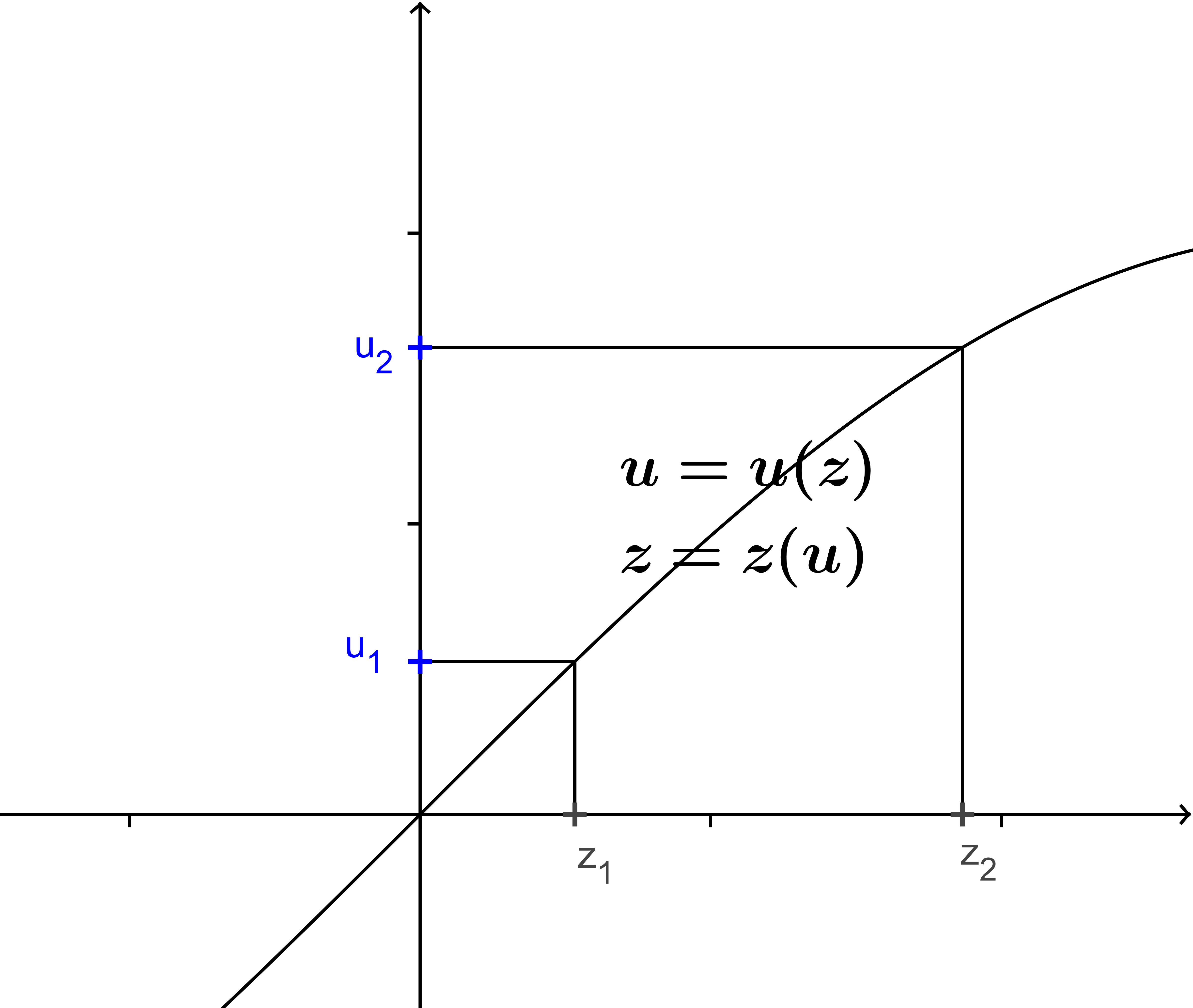
Definite Integration by Parts - A Geometric Interpretation: The formula for integration by parts for the definite integral has an interpretation based on the concept that the integral represents the area of the region enclosed by an axis and the graph of a positive function of the axis variable. Thus `int_{z_1}^{z_2) v(z) dz` represents the area of the region enclosed by the z axis and the graph of v as a function of z while `int_{v_1}^{v_2) z(v) dv` represents the area of the region enclosed by the v axis and the graph of z as a function of v. From Figure VII.C.1 it should seem reasonable that the sum of these two integrals is precisely the region with area

`v_2 z_2 - v_1 z_1`. Or to summarize the result with definite integrals:

Example VII.C.1 (revisited). Recall L'(t) = t e ^-t and L(1) = 0.Figure

First we'll find `L(2) = int_1^2 te^{-t} dt` using integration by parts.
Let `v = t` and `dz = e^{-t} dt`, so `dv = dt` and `z = -e^{-t)`. Then
`L(2) = int_1^2 te^{-t} dt = -te^{-t}| _1^2 + int_1^2 e^{-t}dt = -2e^{-2} + e^{-1} - e^{-2} + e^{-1} = 2/e - 3/(e^2)`

Now we'll find `L(x) = int_1^x te^{-t} dt` using integration by the same parts.
`L(x) = int_1^x te^{-t} dt = -te^{-t}| _1^x + int_1^x e^{-t}dt = -xe^{-x} + e^{-1} - e^{-x} + e^{-1} = 2/e - (1+x)/(e^x)`

Thus as `x ->oo`, we have `L(x)-> 2/e` . [Can you explain why `lim_{x ->oo} (1+x)/(e^x) = 0` ?]

Reduction formulae: Frequently a problem has a form that involves a high power of x and with the use of integration by parts the resulting integration problem has the same form but with a lower power of x. These situations are made easier to resolve with what are called reduction formulae . These formulae can be used to solve some problems without need to repeat the same techniques for many similar integrals. The next example illustrates both the discovery of a reduction formula and its use to simplify the toil in evaluating an integral.

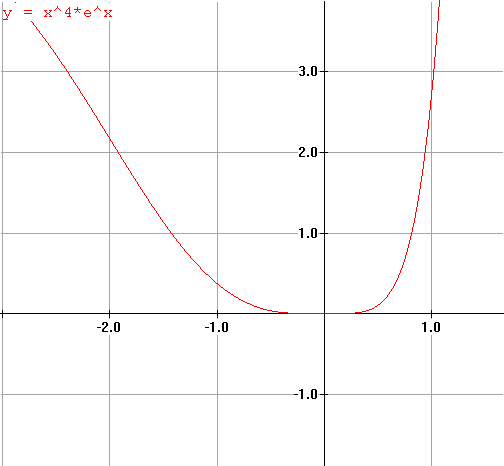
Example VII.C.6. Find the area of the region enclosed by the X-axis, the lines x = 0 and x = 1 and the graph of `y = x^4 e^x` .

Solution: The area of the region described here is expressed simply as a definite integral, namely
`int_0^1x^4 e^x dx`. Rather than do this single integral by itself, we use integration by parts to find a reduction formula for `int x^n e^x dx`  where n is a natural number.

Let `v = x^n` and `dv = e^x dx`, so `dv = n x^{ n-1} dx` and `v = e^x`.
This gives the reduction formula

We now apply this first with n = 4 , and then using n = 3, 2, and 1.

But `int  e^x dx = e^x + C` so we can now proceed to work back to solve the original problem .
[Ignore the constant of integration until the end.]

We can now complete the evaluation of the definite integral for the area problem using the fundamental theorem of calculus.

Exercises VII.C

Find the following indefinite integrals:

For problems 11-16 find the indicated definite integrals a) by finding the appropriate indefinite integral and applying the fundamental theorem of calculus and b) evaluating the individual parts with integration by parts as in Example VII.C.6.

It is sometimes a little confusing in determining whether to use a substitution or integration by parts to find an integral.

In problems 17 to 26, substitution and / or integration by parts methods or neither method may be helpful in finding an answer. Beware.... some of the following integrals have no elementary solution. Check your answer by differentiation.

27. Further investigations of L'(t) = t e ^-t with L(1) = 0.

a) Let Q(t) = t ³ e ^-t. Show that if t > 3 that Q is a decreasing function and hence that for t > 3 , Q(t) < 3 .

b) Using part a) explain why for t > 3, L'(t) < 3/t ² . Explain briefly why as `t -> oo`,  `L'(t) = (t)/(e^t) -> 0`.

c) Use the inequality established in part b) find an upper bound for L(t) for t > 1. Explain your reasoning.

d) Compare the bound found in part c) with the limit for L(t) found in the text. Draw a figure that visualizes these two numbers and discuss the relation to the graphs of L'(t) and 3/t ².

28. (Project) Suppose n is a positive integer and L'(t) = t ⁿ e ^-t with L(1) = 0. a) Find a formula depending on n for L(2).

b) Explain why for each n , as `t -> oo`,  `L'(t) -> 0`.

c) Find and justify a formula depending on n for the limit of L(t) as `t -> oo`.

29. Discuss the geometric (area) interpretation of the formula for integration by parts for definite integrals.

30. The integral of `cos^2(x)`. Fill in the details to justify the following use of integration by parts to find an indefinite integral for `cos^2(x).

31. Find the area of the region enclosed between the X-axis and the graph of `Y = sin^2(x)` between 0 and `pi`.

32. Suppose n is a positive integer. Find and justify a reduction formula for `int (e^x)/(x^ n) dx`. Use your formula to find `int (e^x) / (x^4) dx`.

33. Suppose n is an integer with n > 2. Find a reduction formula that expresses `int cos^n(x) dx`  in terms of  `int cos^{n-2}(x) dx.
Use your formula to find `int_{x=0}^{x=pi/2} cos^5(x) dx` .

34. Suppose k is a positive integer. Find a reduction formula for `int (ln(x))^k dx`.

35. (Project) Let `L(t,n) = int _{x=0}^{x=t}  x^{n-1} e^{-x} dx` where n is a positive integer.
a). Find a reduction formula for L(t,n) in terms of L(t,n-1).
b). Explain why for each positive integer n, as `t -> oo`, the limit of L(t,n) exists.
Let `Gamma(n) -= lim _{t->oo) L(t,n)`. This is called the Gamma function.
c) Find `Gamma(1) , Gamma(2)`, and  `Gamma(3)`.
d) Show that for n any positive integer n, `Gamma(n+1) = n cdot Gamma(n)` .
e) Show that for any positive integer n, `Gamma(n) = (n-1)!`.

36. a. Let `L(A) -= int_{x=0}^{x=1}  (f(x) - Ax)^2 dx` . Show that L takes on its smallest value when `A = 3 int_{x=0}^{x=1} x cdot f(x) dx`.
b. Find the values of A that minimize L(A) in part a)
i) when `f(x)= x` ; ii) when `f(x) = e^x`; iii) when `f(x)=ln(x+1)`.

37. a. Let `g(A) -= int_{x=-pi}^{x=pi}  (f(x) - Asin(x))^2 dx`. Show that g takes on its smallest value when `A = 1/p int_{x=-pi}^{x=pi} f(x) cdot sin(x) dx`.
b. Find the values of A that minimize g(A) in part a)
i) when `f(x)= x`; ii) when `f(x) = e^x`.

38. Recall that `f` is a probability density function for a random variable X on an interval `[a,b]` if `f(x)>0` for `x` and  `int_{x=a}^{x=b} f(x) dx` = 1.
Let `V(A) -= int_{x=a}^{x=b}  (x - A)^2 f(x)dx`. Show that `V` takes on its smallest value when `A = mu_X = int_{x=a}^{x=a} x cdot f(x) dx`.
`mu_X` is called the mean or the expected value of the random variable `X`.
[This will be discussed further in Chapter VIII.*].

a) Find the value of `a` so that `f(x) = e^x` is a probability density function of a random variable on the interval `[0,a]`. Determine the mean for this random variable.

b) Find the value of a so that `f(x) = a sin(x)` is a probability density function of a random variable on the interval `[0,p]`. Determine the mean for this random variable.

39. A generalization of parts. As the examples of reduction formulae show, the method of integration by parts may be used repeatedly to some advantage. In this problem we'll try to find a pattern that can be used to work such examples systematically .

a) Suppose f is a function for which f ' and f '' are continuous functions and g is a continuous function with indefinite integral `g^{**}` and with `g^{****}` an indefinite integral for `g^{**}`.

c) Apply your formula to find `int  x^2 sin(x) dx` and `int x^2 e^x dx`.
d) State and justify a formula that generalizes integration by parts using the k ^th derivative of f.

e) Apply your formula to find `int  x^4 sin(x) dx` and `int x^4 e^x dx`.

40. Apply your formula from the previous problem to the example where f(x) = e ^-x and g(x) = 1.

a)Show that `int e ^{-x} dx = e ^{-x} [1 + x + (x^2)/2 + (x^3)/6] + int (x^4)/24 e^{-x} dx`.

b)By considering `int_0^1 e ^{-x} dx = e ^{-x} [1 + x + (x^2)/2 + (x^3)/6]| _0^1 + int_0^1 (x^4)/24 e^{-x} dx` , find `int_0^1 x^4 e^{-x} dx`.