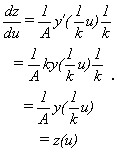VI. Model Related Differential
Equations: The Transcendental Functions. (Web text
in progress.)
© M. Flashman
Preface:
The definitions of polynomial and rational functions are easy to understand.
They use only the arithmetic operations learned in elementary school:
addition, subtraction, multiplication, and division. The definitions of
the exponential, logarithmic, and trigonometric functions are more advanced
and sophisticated requiring an understanding of powers, roots, and geometry
for similar triangles. What makes these latter functions important today
is the fact that they appear in many different modelling contexts. One
way in which these functions arise in models is through the study of differential
equations. The following chart presents a summary of derivative results
for the core functions we have studied together with their related characteristic
differential equations with initial conditions.
|
Function
y = f (x)
|
Derivative
y' = f ' (x
)
|
Differential equation
F(x, y, y', y'')
= 0
|
Initial Conditions
y(a) = b,...
|
|
xn
|
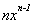
|
xy' - ny = 0
|
y(0) = 0
|
|
sin(x)
|
cos(x)
|
y'' + y = 0
|
y(0) = 0 ; y'(0)
= 1
|
|
cos(x)
|
-sin(x)
|
y'' + y = 0
|
y(0) = 1 ; y'(0)
= 0
|
|
tan(x)
|
|
|
y(0) = 0
|
|
|
exp(x) = ex
|
y'-y = 0
|
y(0) = 1
|
|
ln(x) ... x>0
|
1/x
|
xy'- 1 = 0
|
y(1) = 0
|
Looking at the differential equations
in this table notice that power functions have characteristic differential
equations that are more complicated than those of the other functions on
the table. In this chapter we will explore further how differential equations
are connected to the functions that solve them. To connect these functions
to differential equations more precisely, we will start the first sections
of this chapter by describing some modelling contexts. With each model
we will consider a differential equation defining a solution function for
that model. Studying these solution functions we will recognize them
as familiar functions from properties and issues connected to the
differential equaitions.
VI.A. The Natural Exponential
Function and A Growth Model.
We
begin our study models and differential equations with exponential functions.
First we'll examine a model for populations that is based on a simple discrete
difference equation. Then we will turn our attention to a comparable continuous
calculus model. In our population model we assume we have a population
of biological objects [they may be fruit flies, bacteria, rabbits, owls,
fish, trees, and /or even humans], and this population is changing with
time so that the measure of the population size, P, is a function of time,
t. Note that P(t) may be measured with integers only, as with a population
counter, or it may be measured with real numbers, as with biomass for bacteria,
tonnage for fish, or aggregate height for trees.
|
n
|
P
|
|
0
|
*
|
|
1
|
**
|
|
2
|
* * * *
|
|
3
|
** ** ** **
|
Example
VI.A.1. In a laboratory experiment a single cell breaks into two distinct
cells every 8 hours. Starting with a single cell, this process continues
for 40 hours in the same fashion.
How many cells will be present at the
end of the time period?
If the process continues without change
for t = 8n hours, how many cells will be present at time t?
Estimate how long it will be before
there are over 1000 cells.
Solution:
Let
P(n) be the number of cells present after 8n hours. Then P(0) = 1 expresses
the statement that the experiment starts with a single cell and P(n+1)
= 2 P(n) expresses the statement that every eight hours the number
of cells doubles. Since 40 = 8 . 5, the first question asks
us to find the value of P(5). Following routine calculations we have that
P(1) = 2, P(2) = 4, P(3) = 8, P(4) = 16 and P(5)=32. So if the growth continues
as stated in the problem, 32 cells will be present after 40 hours.
It is not hard to see from the pattern
in these calculations that
P(n) = 2 n when
t = 8n.
This answers the second question.
The last question can be rephrased,
"For what n is 2n >1000?"
Here a quick check on the powers
of 2 shows that 210 = 1024, so n = 10 is the smallest
n that will satisfy the inequality. So P(10) = 210
>1000 shows
we will need to wait about t = 8 * 10 = 80 hours, a little more than 3
days, for there to be 1000 cells.
Comment:
In
the example, the change in populations between 8 hour periods is not difficult
to compute. If we let DP(n)
denote the change in population expressed by the formula P(n+1)- P(n) then
we can observe from the previous computations that P(0) = 1, P(1) = 2,
P(2) = 4 , and
DP(n)
= P(n+1)- P(n) = 2 n+1 - 2 n = 2 n = P(n).
The preceding example illustrates
a model in which the population changes occur "discretely" in the sense
that it is possible to isolate particular instants in time when the changes
occur. The change in population, DP(n),
from
the n th period to the (n+1) st period is determined
precisely to be the value of the population at the end of the n th
period.
The
differential equation model: We now turn our attention to a model for
populations in which the population measure changes as a continuous function
of time. Assume a biological population for which at time
t the
population grows at a rate proportional to the population at that time.
The
growth rate of the population is expressed by the differential equation
P'(t) = k P(t) or dP/dt
= kP,
with
k being the proportionality constant. When t = 0 the population
is P(0), the initial population.
Model units: We have some
flexibility in the choice of the population unit of measurement in this
model, so we will standardize our population measurement unit so that
P(0) = 1. You can think of this standardization as measuring the size
of the population when our observation begins and comparing subsequent
populations in terms of that initial population. In other words, the populations
are measured using the initial population as the unit for scaling.
The population growth rate, P'(t),
is expressed in terms of population units per unit time. Since the unit
of time is not yet determined for our model, we can choose a measurement
for time so that the proportionality constant k is 1. Following this judicious
choice of units we can now study more thoroughly the simpler model differential
equation: P'(t) = P(t) .[See the comments at
the end of this section for a further exploration of the effects
of choosing units.]
In summary then, the
population size in our model is characterized mathematically as a particular
solution to the differential equation P'(t) = P(t) with the initial condition
P(0) = 1.
Visualization: Using the
ideas of tangent fields from Chapter
IV.D, we begin to understand the differential equation P'(t) = P(t)
by sketching its tangent field.[See Figure 1.]By focusing attention on
the initial condition, P(0)=1, we obtain a rough sketch of the graph of
the solution function as an integral curve for this field.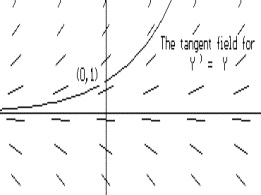
The
integral curve sketch confirms some information which the derivative gives
us, namely, that P is increasing when P(t)>0 and that the graph of P is
concave up [since P"(t) = P'(t) = P(t)] when P(t)>0. This information allows
us to conclude further that the population in this model is increasing
at ever increasing rates.
Estimating
P(1): One immediate issue for this model is to learn the value of P(1).
This will tell us the size of growth from one unit of population over one
unit of time. We start to estimate P(1) using Euler's method with n = 4,
so Dt
= 1/4 and dP(t) = P'(t) Dt
= P(t) 1/4. Here are our calculations in a table:
|
x
|
P
|
P ' = P
|
dP = .25P
|
|
0
|
1
|
1
|
0.25
|
|
0.25
|
1.25
|
1.25
|
0.3125
|
|
0.5
|
1.5625
|
1.5625
|
0.390625
|
|
0.75
|
1.953125
|
1.953125
|
0.48828125
|
|
1
|
2.44140625
|
|
|
You can work with this further yourself using a
speadsheet.
It is also worth looking at these calculations with a little more subtle
technique, factoring as we go:
P(0) = 1
P(1/4) »
P(0)+ P'(0) . 1/4 = 1 + 1 . 1/4 = 5/4
P(2/4)»
P(1/4) + P'(1/4) .1/4 »
5/4 + 5/4 . 1/4 =(5/4) 2
P(3/4) »P(2/4)+P'(2/4)
.1/4 »
(5/4) 2+(5/4) 2 . 1/4=(5/4) 3
P(1) »(3/4)
+ P'(3/4) .1/4 »
(5/4) 4 »2.4414
Okay.
So our first estimate using Euler's method with n = 4 is that P(1) »
2.4414. But we can do better than that, much better.
Note
that since P'(t) = P(t), P(a + Dt)
» P(a) + P(a) Dt
= P(a)(1 + Dt)
.
If we use Dt
= 1/n for n, a positive integer, then P(1/n)»
1 + 1 . 1/n, P(2/n) »P(1/n)
+ P'(1/n) . 1/n = (1+1/n)2 and continuing in this
fashion we obtain
P(1) = P(n/n) »
(1+1/n) n.
For n very large, Dt
=1/n will be close to 0 and we should obtain a much better approximation
for P(1) from Euler's method. In limit notation we write
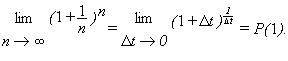
Using this estimation with n = 1000,
we obtain P(1)»(1+.001)1000
»
2.7169 and with n = 10,000, we find P(1) »
(1.0001)10000 »
2.7181. With n = 10 6, P(1) »
(1+10 -6)1,000,000»
2.718280469.
[In
fact, the convexity of P helps explain why these are all underestimates.
Can you see why?]
You may recognize from these estimates
that the exact value of P(1) is a number studied in your pre-calculus work.
It is a mathematical constant which has been of interest for hundreds of
years and, like the number p,
has a special symbol attached to it, e
. [Actually the letter e
was first used to represent this constant extensively by Euler, whose textual
treatment of both pre-calculus and calculus topics were the standard for
many years.] Thus, by notational convention and our previous estimates
we have that P(1) = e »
2.718 .
Properties
of P: We turn now to explore some of the important features of P as
a function. If it takes one unit of time for one unit of population to
grow to be e units of population, you might expect that in
one unit of time any population size will grow by a factor of e.
Conjecture:
For any t, 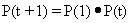 .
.
Comment:
We can make more sense of this conjecture from our previous use of Euler's
method:
Since P(t + Dt)
»
P(t) + P(t) Dt
=P(t)(1+Dt)
so P(t + n Dt)»P(t)(1+
Dt)n.
With Dt=1/n
this shows that P(t+1)=P(t+ n 1/n)»P(t)(1+1/n)n.
When n is large we can see why 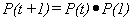 .
.
Proof
of Conjecture: We can prove that the conjecture is true for all t in
a more rigorous fashion by considering the function F(t) = P(t+1)/P(t)
.
Using
the quotient and Chain Rules we find F '(t) .
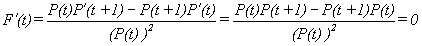 .
.
So
[by Theorem IV.**,] F(t) is a constant function, i.e., F(t)
= K for all t.
But
using t = 0, we see that F(0) = P(0+1)/P(0) = P(1)/P(0) = e/1 = e.So, 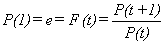 for
all t, or
for
all t, or  .
.
EOP.
Comment:
Note
how this equation was proven. First we examined a related function Fand
showed that F was a constant function because F '(t) = 0. Then we used
the particular value of F when t = 0 to find the constant, allowing us
then to prove the original equation was true.
From the conjectured and now proven
equation we see that
P(2) = P(1+1) = P(1) .
P(1)
= e . e = e 2;
P(3) = P(2+1) = P(1) . P(2)
= e . e 2 = e 3;
and
in general we can show (using mathematical induction) that for any
natural number n,
P(n) = e n .
It
appears that P is the exponential function with base e. [1]We
proceed now to justify that P satisfies the usual properties of exponents
using only its characterization from the differential equation. [These
results are also suggested by further exploration of Euler's approximations
for the values P(n) and the definition of e. See Exercise
14.]
Theorem
VI.A.1 Suppose s and t are real numbers and P is the solution to the
differential equation P'(t) = P(t) with P(0) = 1. Then
(b) P(-t)
= 1/P(t),
(c) P(s-t) =
P(s)/P(t), and
(d) P(rt)=[P(t)]r
when r is an rational number.
PROOF:
(a)
We proceed as we did in justifying the previous conjecture.
Let 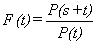 then
then 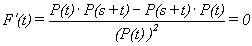 so F(t) = K for some constant K.
But
so F(t) = K for some constant K.
But 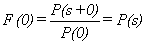 .
.
Hence 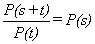 or
P(s+t)
= P(s) . P(t) .
or
P(s+t)
= P(s) . P(t) .
(b)
P(t+(-t)) = P(0) = 1 but by (a) P(t+(-t)) = P(t)P(-t) so 1 = P(t)
.
P(-t) OR P(-t) = 1/P(t).
(c)
P(s-t) = P(s+(-t)) = P(s) . P(-t) = P(s) . 1/P(t)
= P(s)/P(t).
(d)
Consider F(t) = [P(t)] r/P(rt) then
 .
.
so
F(t) = k for some constant k.
But
F(0)=[P(0)] r/P(r.0)=1r/1=1 so 1=[P(t))]
r/P(rt)or P(rt) = [P(t)] r.
EOP.
Defining
the natural exponential function: We could give a definition for the natural
exponential function characterizing it solely as the solution to the differential
equation y'=y where y(0)=1. Defining a function by declaring it to be the
unique solution to a differential equation is not as unusual as it may
seem. Recall that in the motion interpretation for the derivative a differential
equation can be interpreted as giving a way to determine the velocity of
a moving object from the time and its position. Knowing the velocity of
the object at any time and position would seem to enable us to determine
its position at any time just from knowing its position at one time.
|
Comments:
1. P(t)=e t :
Applying the last part of the theorem to an rational number r, we see that
P(r) = P(1) r = e r. Since P is a continuous function,
this shows that P has the same values as the exponential function with
base e for any real number t, so we can write P(t)=e t for
any real number t. Recognizing this identification of P with the exponential
function of base e, we express the key facts we have demonstrated about
P using the Liebniz notation for the derivative and the exponential notation
as follows:
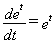 ;
e 0=1; and e 1 =e.
;
e 0=1; and e 1 =e.
Also
(a) e s+t = e
s.e t;
(b) e -t =1/e
t;
(c) e s-t = e
s/e t;
(d) e r t = (e
t) r.
2.Asymptotes: Note that since
e > 2 , e 2 > 2 2 , e 3 > 2 3and
generally e n > 2 n. So when n is very large,
e n is very large as well. This fact is expressed as a limit
statement by writing
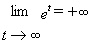 .
.
Also,
since e -n = 1/e n , when n is very large , e
-n is the reciprocal of a large number. Thus for large choices
of n, e -n » 0.
This is expressed as a limit statement by writing
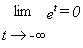 .
.
On
the graph of P(t) = e t this last fact is recognized by the
horizontal asymptote of the graph with the X - axis.
3.
Looking at integration: Since 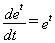 we
can write the indefinite integral form of this statement as
we
can write the indefinite integral form of this statement as 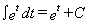 .
.
4.
Existence: The preceding discussion assumed that there was a solution
to the differential equation y' = y with y(0) = 1. The existence of a solution
is certainly suggested by the tangent field and the computations using
Euler's method. A rigorous demonstration of the existence of this function
independent of any assumptions about exponential functions and their properties
will be given later in this chapter. For now, all the evidence we have
assembled suggesting the conclusion should suffice.
5.Other
models: The general issue of population models and differential equations
is studied in greater depth in more advanced courses in differential equations
and mathematical modeling. The differential equation y' = ky with
initial condition y(0) = A is very important to the study of numerous other
real situations besides this simple population growth model. In
exercise 8 below you are asked to check that the general solution of
this differential equation is y = A e kt .
6. Changing
units to normalize the model:
[This next comment is pretty tricky. Be sure to read this with a pencil
and paper at hand to make sure you follow the changes in the units.]
As suggested initially, a suitable
choice of units shows the relation of the special case when k = 1 and A
= 1 to the general situation with y'(t)=ky(t) and y(0) = A.
Here's how: Suppose the units for
y are called yugs and the time t is measured in tocks.We'll let A yugs
be our new unit for measuring the population with the variable z,
which we'll call zugs, so A yugs is one zug. We'll let 1 / k tocks be our
new time units, we'll call them nocks, and we'll uses u to measure the
time in nocks, so k nocks is one tock. So y = A z and t =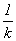 u.
u.
Now what is the relation between
the measure of the population measure as y yugs at time t tocks, y(t),
and the measure of the same population measure as z zugs at the same time
but measured as u nocks, z(u)? Well, Az(u) expresses the measure of the
population in yugs based on its measurement in mugs,while y(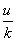 )
expresses the measurement of the population at the same time measured in
tocks also in the units of yugs. So Az(u) = y(
)
expresses the measurement of the population at the same time measured in
tocks also in the units of yugs. So Az(u) = y(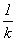 u).
Now we suppose that y(0)=A, so Az(0)=y(0)=A and z(0)=1. Furthermore since
z(u) = 1/ A y(
u).
Now we suppose that y(0)=A, so Az(0)=y(0)=A and z(0)=1. Furthermore since
z(u) = 1/ A y(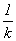 u)
and we assume y'(t)= ky(t), we have
u)
and we assume y'(t)= ky(t), we have
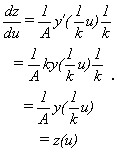
So
if y satisfies the original differential equation y '= ky then
z satisfies the differential equation z' = z with z(0) = 1.But our work
has shown then that z(u) = e u. Now translate this back into
a statement about y:
Az(u) = y(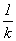 u)
where
u)
where 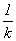 u
= t.
u
= t.
So y(t) = A z( kt ) = A e kt.
7. Other Applications of y'=ky
with y(0) = A
There are many other situations
where the differential equation beginning this section arises in expressing
the rate of change of a measured quantity. One important application is
to the measurement of the amount of radioactive material present in a given
mass of material. Because of the nature of unstable radioactive matter,
the rate of change (decay) of the matter is assumed to be proportional
to the amount of matter present at the specified time. This should make
some sense from a physical point of view. With less unstable material present
there is less opportunity for the interaction of unstable particles to
produce further radioactive decay.
Another
situation involving this basic differential equation concerns the change
in temperature of one object in a medium which remains at a constant temperature.
In this context we find a physical context to which one of Newton's laws,
called his law of cooling, applies. The law says that the rate
of change of the temperature is proportional to the difference in temperatures
of the object and the medium.These situation will be explored further
in the exercises of section VI.D.
The
exercises for this section apply many of the concepts and techniques we
have developed already in the earlier chapters to a further exploration
of the exponential function and functions that use the exponential function
in their definition.
Exercises
VI.A.:
1.
Find
the derivatives of the functions as indicated. [Don't forget the chain
rule!]
a. f(x) = exp ( 5x ) . Find
f '(0) , f '(1) and f '(t).
b. f(x) = exp ( -x ) . Find
f '(0) , f '(1) and f'(t).
c. f(x) = exp ( x 2)
. Find f '(0) , f '(1) and f'(t).
d. f(x) = exp (-x 2)
. Find f '(0) , f '(1) and f'(t).
e. f(x) = exp (sin(x)).
Find f '(0) , f '(p)
and f '(t).
2. Find the derivatives of the
functions as indicated. [Don't forget the chain rule!]
a. y = e 3x .
Find dy/dx when x = 0 and 1.
b. y = x e x.
Find dy/dx when x = 0 and 1.
c. y = e x sin(x).
Find dy/dx.
d. y = e x +e
-x. Find dy/dx when x = 0.
e. y = e x -e
-x. Find dy/dx when x = 0.
3.
Find
the derivatives of the functions as indicated. [Don't forget the chain
rule!]
b. Find D t(exp(t
2 - 1)).
c. Find D t(
exp(t sin(t) ) ).
e. Find D t(sec(e
2t ) ).
4.
Sketch
a graph of y = exp(-x 2 / 2) showing all extrema and points
of inflection. Explain your work using first and second derivative analysis.
5.
Sketch
a graph of y = x e -x showing all extrema and points of inflection.
Explain your work using first and second derivative analysis.
6.
Sketch
a graph of y = x 2 e -x showing all extrema and points
of inflection. Explain your work using first and second derivative analysis.
7.
Sketch
a graph of y = sin(x) e -xfor x e
[0,4p],
showing all extrema and points of inflection. Explain your work using first
and second derivative analysis.
8.
Show
that y = A e kx is a solution to the differential equation y'=ky
with y(0) = A.
9.
Show
that y = e x (sin(x)+cos(x)) is a solution to the differential
equation y' = 2 e xcos(x) and y'' - y' = -2e xsin(x).[Corrected
9-9-02 4:30 pm ]
10.
Show
that y=e x(sin(x)+cos(x)) is a solution to the differential
equation y''-2y' +2y = 0.
11.
Suppose
f(x) = k e x is the probability density function for a random
variable X on the interval [0,1]. Show that k = 1/(e-1).
12.
Suppose
f(x) = k e -x is the probability density function for a random
variable X on the interval [0,1]. Find k .
13.
Find
the following indefinite integrals:
| a. ò e3x
dx |
c. ò cos(x) esin(x)
dx |
| b.ò x exp(x2
)dx |
d. ò ex
sin(ex )dx |
14.
Use
Euler's method to explain why when n >> 0, (1+1/n) 2n »
e
2, (1+1/n) 3n »e
3,
(1+1/n) 4n »
e
4, and in general (1 + 1/n) kn »
e k.
15.
Find
the following definite integrals. You may express your answer using the
number e.
a.
ò01 e3x
dx
b. ò01 x
exp(x2 )dx
16.
Find
the area of the region enclosed by the graph of Y= e x = exp(X),
the X axis, X= -1, and X= 1.
17.
The
area of the region enclosed by the graph of 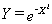 ,
the X axis, X= -1, and X= 1 is often of interest in the study of probability
and statistics. Estimate this area using Euler sums with a. n=4. b. n=8.
c. n = 100.
,
the X axis, X= -1, and X= 1 is often of interest in the study of probability
and statistics. Estimate this area using Euler sums with a. n=4. b. n=8.
c. n = 100.
18.
The
region in the plane bounded by the graph of 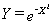 ,
the X-axis, the Y axis, and the line X=1 is rotated about the Y- axis to
form a region in space.Find the volume of this spatial region
,
the X-axis, the Y axis, and the line X=1 is rotated about the Y- axis to
form a region in space.Find the volume of this spatial region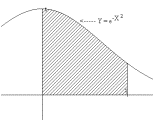 .
.
19.
The
region in the plane bounded by the graph of 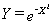 ,
the X-axis, the Y-axis, and the line X= t is rotated about the Y- axis
to form a region in space.Find the volume of this spatial region.Give an
estimate for the volume of the this region in space when t = 100.
,
the X-axis, the Y-axis, and the line X= t is rotated about the Y- axis
to form a region in space.Find the volume of this spatial region.Give an
estimate for the volume of the this region in space when t = 100.

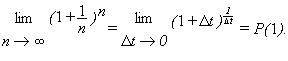
![]() .
.
![]() u.
u.
![]() )
expresses the measurement of the population at the same time measured in
tocks also in the units of yugs. So Az(u) = y(
)
expresses the measurement of the population at the same time measured in
tocks also in the units of yugs. So Az(u) = y(![]() u).
Now we suppose that y(0)=A, so Az(0)=y(0)=A and z(0)=1. Furthermore since
z(u) = 1/ A y(
u).
Now we suppose that y(0)=A, so Az(0)=y(0)=A and z(0)=1. Furthermore since
z(u) = 1/ A y(![]() u)
and we assume y'(t)= ky(t), we have
u)
and we assume y'(t)= ky(t), we have
 .
.