Chapter V. C Three Major Theorems of (Definite) Integral Calculus
The Fundamental Theorems of Calculus [Draft - in progress]
© 2014 M. Flashman

Preface: In Chapter IV sections F and H, we introduced two results described as fundamental theorems of calculus.
Theorem IV.3 in IV.F showed how to determine the area of a planar region bounded by the graph of a positive continuous function, $v,$ the lines $X= a, X=b$,  and the X-axis. Using any primitive function (indefinite integral) $S$ for $v$, [i.e., $S'(t)=v(t)$ for all $t$,] the area is $S(b)-S(a)$.

Theorem IV.4 described a situation where a positive continuous function was given on an interval and the issue was whether there was a primitive function (indefinite integral) $F$ for $P$. The result was that there was such a primitive function and in fact one could describe that primitive function $F$ as a function of the number $t$ determined geometrically as the area of  the region enclosed by the X-axis, the line $X=A$, the line $X=t$, and the graph of the function $P,$ i.e., the graph of $Y = P(X)$. See Figure V.C.1

 Theorem IV.3:  Suppose that $v$ is a positive function continuous on $[a,b]$ and $S$ is an antiderivative for $v$ on $[a,b]$.  Let $A$ be the area of the region enclosed by the graph of $v(t)$,  the lines  $X=a,  X=b$, and the X-axis. Then $A = S(b) - S(a)$. 
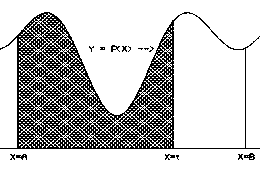
Theorem IV.4 THE FUNDAMENTAL THEOREM OF CALCULUS FOR DIFFERENTIAL EQUATIONS (first draft). If $P$ is a positive continuous function on $[A,B]$,  then there is a function $F$ with $F'(t) = P(t)$ for all $t$ where  $A<t<B$.  In fact, $F$ can be defined at $x = t$ to be the area of the region enclosed by the X-axis, the line $X=A$, the line $X=t$, and the graph of the function $P$, i.e., $Y = P(X)$. See Figure V.C.1


Both these results connect the issues of derivatives (anti-derivatives  and primitives) and areas in a geometric context. The results extend as well to a much wider class of contexts through the concept of the definite integral introduced in IV.A. In this section we will discuss the restatements of these two important results using the definite integral and introduce a third major result about the definite integral that is important for its own purposes and that can be used to justify the other two results. These three results form a logical network supporting much of the theory of differential equations and integration. Besides a logical foundation, these theorems also provide heuristic support for the power that approximating sums and derivatives can bring to understanding and making sense of their many applications.

We'll begin with a restatement of the Derivative Form of the Fundamental Theorem now omitting the condition that $P$ be a positive function that was used to form the area function of the proof of theorem IV.4. This area function is replaced in the restatement by a definite integral.
Theorem V.C.1 Fundamental Theorem of Calculus I. (Derivative Form):
Suppose  $P$ is a continuous function on an interval, $I$, with $A$ any number in that interval. For any number $t$ in $I$, define the function $S$ by $S(t) = \int_A^t  P(x)  dx$. Then for any $c$ in $I$, $S'(c)= P(c)$.
Proof: We will give a proof of this result later in this section.
Next comes the Evaluation Form of the Fundamental Theorem. Once again we remove the requirement that the function be positive and we replace the area concept with a definite integral.
Theorem V.C.2 Fundamental Theorem of Calculus II. (Evaluation Form):
Suppose $P$ is a continuous function on an interval, $I$,  with $a$ and $b$ any numbers in $I$, and $F$ is an antiderivative (indefinite integral or primitive function) for $P$, i.e., $F'(t)=P(t)$ for all $t$ in $I$. Then $\int_a^b P(x) dx = F(b) - F(a)$.
Proof: For this argument we will use the Fundamental Theorem of Calculus I as just stated.
Using $A= a$ in that result we let $S(t) = \int_a^t  P(x) dx$ so that $S'(t) = P(t)= F'(t)$ for all $t$ in $I$.
Now by Theorem IV.B.2, which said that functions with the same derivative differ by a constant, there is a constant $K$ so that for any $t$ in $I$,
$S(t) = F(t ) + K$.
But using the basic properties of the definite integral  we see that
$S(a) = \int_a^a  P(x)  dx = 0  = F(a) + K$.
We solve this last equation for the value of $K$, finding $K = - F(a)$.
 Hence, $S(t) = F(t) - F(a)$ for all $t$ in the domain.
Finally we put the definition of $S$ together with this last result to see that  $\int_a^b P(x)  dx  =  S(b) =  F(b) -  F(a).$    EOP.
Comment: Watch out! What we are showing in this stage is that if Theorem V.C.1 is true, then Theorem V.C.2 must also be true. Theorem V.C.2 will not be fully justified until we have demonstrated Theorem V.C.1.
The third major theorem of the integral calculus is often interpreted as related to averages and is therefore referred to as a Mean Value Theorem for integrals. See Figure V.C.2
Theorem V.C.3 The Mean Value Theorem for the Definite Integral.
Suppose $P$ is a continuous function on $[a,b]$. Then for some $c \in (a,b)$
   $P(c) [b-a] =    \int_a^b P(x) dx $
or
$P(c) = \frac {\int_a^b P(x) dx }{b-a}$.

 Figure V.C.2  visualizes $P(c) [b-a]$ as a rectangle with area  equal to $ \int_a^b P(x) dx$. $P(c)$ is sometimes described as "the average value of $P$."
Figure .C.2 MVT for Definite Integral
Figure V.C.2
We will present two separate arguments to justify Theorem V.C.3. We do this to show some of the ways in which results in mathematics can be intertwined in a web of logical connections. In the first proof, we will assume that both fundamental theorems of calculus are true, while in the second we will give a justification based on more elementary properties of the definite integral.
Proof of Mean Value Theorem for the Definite Integral (1) :
Recall the statement of the Derivative Mean Value Theorem (see section III.B) for a function $f$ on the interval $[a,b]$ said that if $f$ is continuous on $[a,b]$ and differentiable on $(a,b)$ then there is a number $c\in (a,b)$ where $f'(c) [b-a] = f(b) - f(a)$. Now replace $f$ by the function $S$ in this statement where $S(t) = \int_a^t P(x) dx$ as in the Fundamental Theorem Derivative Form so that $S'(c)=P(c)$. Now just check: $P(c) [b-a] = S'(c) [b - a] = S(b) - S(a) =  \int_a^b P(x) dx$  from the Evaluation Form of the Fundamental Theorem.                               EOP
Proof of Mean Value Theorem for the Definite Integral (2):
Since $P$ is a continuous function on $[a,b]$ there are points $c^*$ and $c_*$ where
    $P(c_*) = m ≤ P(x) ≤ M = P(c^*)$ for all $x \in [a,b]$. 
Using the monotonicity property we have $\int_a^b m dx \le \int_a^b  P(x) dx \le\int_a^b M dx$ so that $m \cdot [b-a] \le \int_a^b P(x) dx \le M \cdot [b-a]$. 
This allows us to consider the integral is an intermediate value for the continuous function $f(z) = z [b-a]$ on the the interval between $m$ and $M$.
Consequently for some $z_*$ between $m$ and $M$, $f(z_*) = z_*[b-a] = \int_a^b P(x) dx$.
But since $z_*$ is between $m$ and $M$ and $P$ is a continuous function, there must be some $c$ between  $c_*$  and $c^*$ where $P(c) = z_*$.
Thus we have $c \in (a,b)$ where bold $P(c) [b-a] = \int_a^b P(x) dx$.        EOP
Comment: Though the first proof of the Integral Mean Value Theorem and the proof of the Evaluation Form of the Fundamental Theorem of Calculus have been established by arguments that do not rely on any interpretation of the mathematical objects involved, the formality of the arguments and the reliance on other theorems in the proofs make these arguments abstract and perhaps less informative as explanations of why these results are true. 
The second proof of the integral mean value theorem does not rely on the fundamental theorems of calculus. Instead it uses more elementary results: the monotonicity property of the definite integral and the intermediate value theorem for continuous functions. Arguments built on more elementary (and sensible) foundations are sometimes more convincing, especially if these arguments can be connected to some visual understanding. See Figure V.C.3.
Figure V.C.3 
The GeoGebra figure below shows an example using both a mapping diagram and a graph with  $y = m = Min P$, $ y = M= Max P$, and the other numbers as in proof (2). Note: The number denoted $c_*$ in this figure is the number $c$ in the proof.
You can move the slider values to change the interval $[a,b]$ and enter other functions in the box to see other examples. [Note: This figure works for some, but not all other function examples.]
The point $c_*=...?$ on the mapping diagram can be moved to see how the values of $P$ vary and verify the extreme values of $m$ and $M$ on the mapping diagram.

Download GeoGebra file
Martin Flashman, 9 July 2018, Created with GeoGebra

With the integral mean value theorem justified independently, we now present a proof of the Fundamental Theorem of Calculus in the derivative form. This is essentially Barrow's Theorem which was discussed in Chapter 0 as a result known by Isaac Barrow in a geometric form prior to the development of the calculus by Newton and Leibniz.
Theorem V.C.1 Fundamental Theorem of Calculus I. (Derivative Form):
Suppose  $P$ is a continuous function on an interval, $I$, with $A$ any number in that interval.
For any number $t$ in $I$, define the function $S$ by $S(t) = \int_A^t  P(x)  dx$. Then for any $c$ in $I$, $S'(c)= P(c)$.

Proof: (Based on the Mean Value Theorem for the Definite Integral which has been justified independently.) 
To find the derivative of $S$ at $c$ we return to the definition of the derivative and begin  and the "four step " method.
Step I: By the definition of $S$ we have 
$S(c+h) = \int_a^{c+h} P(x) dx$  and 
$S(c) = \int_a^c P(x)dx$.
Step II. Now it is the addition property of definite integrals tells us that $\int_a^{c+h} P(x) dx  = \int_a^c P(x)dx  +  \int_c^{c+h}  P(x) dx.$ So by a simple subtraction then we have found the difference of these expressions given by
$S(c+h) - S(c)  = \int_a^{c+h} P(x) dx - \int_a^c P(x)dx = \int_c^{c+h}  P(x) dx$ .
Applying the mean value theorem for integrals to this last integral says there is a number $t_*$ between $c$ and $c+h$ where $P(t _*)[(c+h)-h] =  P(t_*) h = \int_c^{c+h} P(x) dx$. 
So we can simplify the difference $S(c+h) - S(c)$ by expressing it as $P(t_*) h$ where $t_*$ is between $c$ and $c+h$, i.e.
$S(c+h)-S(c)=P(t_*) \cdot h$.
Step III. Dividing by $h$ we have
   $\frac{S(c+h)-S(c)}h = \frac {\int_c^{c+h}  P(x)dx } h \\  \ \ \ \ \ \ \ \ \ =  \frac{P(t _*) \cdot h} h = P(t _*)$

Step IV:We consider what happens when $h \rightarrow 0$. Since $t_*$ is between $c$ and $c+h$, $t_*$ must approach $c$. Now by the continuity of $P$, $P(t_*) \rightarrow P(c)$. Put this last result together with the definition of the derivative and we see that $\frac{S(c+h)-S(c)}h =  P(t _*) \rightarrow P(c)$.     So $S'(c)= P(c).$            EOP.
Space for figures to visualize proof of V.C.1
 
 
Figure IV.H.iv 

 


 
Figure IV.H.v 

Download GeoGebra file
Martin Flashman, 9 July 2018, Created with GeoGebra

Examples: Now that we have established these fundamental theorems, we can look further into some simple examples of their use. These examples are not meant to be profound, only to show some of the more rudimentary uses of the results.
1. Using Theorem V.C.2 to evaluate a definite integral.
Find $\int_0^{\frac {\pi} 2} \cos(x) dx$.
Solution: Since $\sin'(x) = \cos(x)$ we have that
    $\int_0^{\frac {\pi} 2} \cos(x) dx  =  \sin(x) |_0^{\frac {\pi} 2} =  \sin( \frac {\pi} 2) - \sin(0) = 1.$
2. Using Theorem V.C.1 to evaluate a derivative.
Suppose that $g(t)= \int_0^t  \frac 1{1 + x^2} dx$.
a) Find $g'(3)$. b) If $F(t)=g(\tan(t))$, find $F'(t)$.
Solutions: a) Using the Theorem V.C.1,   $g'(t)=  \frac 1{1 + t^2}$ so $g'(3)=  \frac 1 {1 + 3^2} = \frac 1 {10}$.
b) Here we use the chain rule, so that $F'(t)=g'(\tan(t)) \cdot \tan'(t) = \frac 1 {1+\tan^2(t)} \cdot \sec^2(t)= \frac 1{\sec^2(t)} \cdot \sec^2(t) = 1$.

Differential Equations: Existence and Uniqueness.

Theorem V.C.1 states that when $P$ is a  continuous function then the differential equation $F'(t) = P(t)$ has a solution. This result can be described as an "existence" result since it declares that "a solution to the differential equation does exist. "

After the work with tangent fields, Euler's method, and the heuristic arguments about the trip from Chapter IV, the result should not come as a surprise.
It is important because it allows us discuss solutions to differential equations even when they have no simple description as elementary functions.

Theorem V.C.2 has a different message, building on the ability to solve the differential equation $F'(t) = P(t)$. It declares that solving the differential equation and computing the net change $F(b)- F(a)$ can be interpreted in other contexts, like area, where measurement can be estimated in a systematic way using sums of the form  $$P(x_0)\cdot \Delta x + P(x_1)\cdot \Delta x  + P(x_2)\cdot \Delta x +...+ P(x_{ n-1})\cdot \Delta x  = \sum_{k=0}^{k=n-1} P(x_k) \cdot \Delta x $$. 

We can rephrase this result with a focus on the value $F(b)$. It says that value of a solution to the differential equation at $x=b$ is completely determined by the value at $a$, $F(a)$ and function $P$. In other words a solution to the differential equation $F'(t)=P(t)$ is determined uniquely by the equation and an initial or boundary condition. It is in this way that Theorem V.C.2 is considered a "uniqueness" result. 

Problems. In problems 1 through 6, use Theorem V.C.2 to find the indicated definite integral.
  1. $\int _0^1 x^2 dx$
  2. $\int _0^1 x^2 + x dx$
  3. $\int _0^1 16 - x^2 dx$
  4. $\int _0^1 x^5 dx$
  5. $\int _0^1 x^n dx$

    6. For the functions in problems 7 through 12, use Theorem V.C.2 to find the indicated definite integral.

  6. $\int _1^3 x^3 dx$
  7. $\int _1^3 x^2 dx$
  8. $\int _1^3 x^2 + x dx$
  9. $\int _1^3 16 - x^2 dx$
  10. $\int _1^3 x^5 dx$
  11. $\int _1^3 x^n dx$
  12. $\int _0^{\frac{\pi}2} \sin(x) dx$.
  13. $\int _0^{\pi} \sin(x) dx$.
  14. Find the value of t so that $\int _0^t x^3 dx = 4$.
  15. Suppose that $F$ is any function with $F'(t) = t^2 + 1$. Show that the area of the region enclosed by the $X$ -axis, the lines $X = 1, X = 5$ and the graph of the function $Y = X^2 + 1$ is  $F(5) - F(1)$.
  16. Suppose $g(t) = \int_0^t (\sin(x^2 ) + 2 )  dx$.
    1. Write a short exposition based on the work in chapter IV on this function. Include in your essay a discussion of the various ways to visualize and estimate the values of g.
    2. Suppose f  is a solution to the differential equation f ' (x) = sin(x2 ). Give an equation relating  f  to the function g in part a. [Hint: What can you say about the difference g(x) - f(x)].

  17. Suppose $A(t) = \int _0^t \frac 1{1 + x^2 } dx$. Draw a figure that illustrates $A(t)$ as an area of a region in the plane for $t > 0$.

[1] In fact this result can also be interpreted geometrically. It says that the slope of the tangent line to the graph of the area function F at the point (t, F(t)) is precisely the value of the function P(t). This connects this form of the Fundamental Theorem to Barrow's Theorem in Chapter 0.