| Theorem IV.4 The Fundamental Theorem of Calculus
For Differential Equations (first draft).
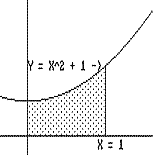
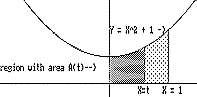
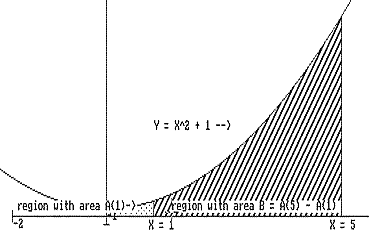
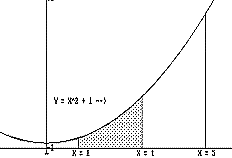
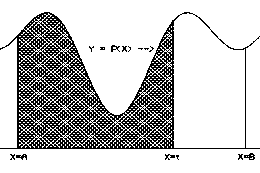
[See Figure IV.H.i.] If P is a positive continuous function on [A,B], then there is a function F with F'(t) = P(t) for all t where A<t<B. In fact, F can be defined at x = t to be the area of the region enclosed by the X -axis, the line X=A, the line X=t, and the graph of the function P, i.e., Y = P(X)[1] |
 |
| Comment: At this stage the details of the proof of Theorem IV.4 are not essential. The proof, given in IV.H Appendix, follows the general outline of the argument of Example IV.G.3. In our discussion so far we have used the notion of area of a planar region in an informal and intuitive sense. In Chapter V we will generalize our experience with area and Euler's method. This will give a more firm foundation to our use of area as an interpretation. A more general formulation will also allow other interpretations to take advantage of the mathematical results expressed in the Fundamental Theorems of Calculus as presented in Theorems IV.3 and IV.4. | |