Chapter IV.E Euler's Method
Sept., 2008: This page now requires Internet Explorer 6+ MathPlayer or Mozilla/Firefox/Netscape 7+.
Revision in progress 3-4-2017 to use SAGE and GeoGebra.
IV.E. Approximating The Solution to A Differential Equation with Initial Condition.
Euler's Method. (Best Viewed with Netscape 6.0 or higher)
©M.Flashman, 2000
Preface: There are some differential equations that are easy to solve. However, for many more differential equations we cannot describe the solutions easily using elementary functions. In Section IV.D we exploited the geometrical interpretation of the derivative to develop tangent (direction) fields with their corresponding families of integral curves. We also saw in Section IV.D that the tangent field enables us to see many qualitative features of a differential equation and its solutions.

In this section we will introduce another important tool for understanding differential equations in the context of an initial value problem. In an initial value problem we are given a differential equation together with an initial condition. Our problem is to describe the particular solution function determined by the given information. Unfortunately, it is rarely possible to find an explicit description of the solution function except in the easiest cases. In most of the harder cases the problem becomes that of finding a good estimate for the value of the solution function. One approach, which we will not pursue here, is to make a sketch of the solution using tangent field and integral curve tools (from section IV.D) and then use that sketch to estimate the desired function value. Instead, we will extend the  concept of the linear (or differential) estimate to a more general tool.The basis remains knowing the value of the derivative at a particular point. 

Review of The Differential: Recall that knowledge of the value of a function and its derivative at a single point can help us approximate the value of the function at a second point. The technique for this approximation was discussed in Chapter III in the section on the differential. There we developed the formula

f (a + h) ≈ f (a) + f '(a) . h
or using the differential dx = h and dy= f '(a) .dx,
f (a + dx) ≈ f (a) + dy = f (a) + f '(a) .dx .

We also gave geometric, dynamic, and economic  interpretations to this approximation. You might review that section quickly now, since we will use those ideas again to find numerical estimates for the solution of a (first order) differential equation with initial condition. This new method based on the differential estimate is called "Euler's method."

Prelude: The following example may seem simple, but if you understand its reasoning you should have little difficulty with its generalization to Euler's method.

EXAMPLE IV.E.1: Suppose f '(x) = x 2 and f (1) = 3. Estimate f (2) using the differential. Use f '(2) and your estimate of f (2) to estimate f (3).

Solution: Since 2 = 1 + 1 we can use the differential with a = 1 and h = dx = 1. We use the differential equation f '(x) = x 2 to find that f '(1) = 1 2 = 1.

Thus f (2) = f (1+1) ≈f (1) + f '(1) . 1 = 3 + (1)1 = 4.

Now 3 = 2 +1, so we continue to estimate again, this time finding f '(2) = 2 2 = 4

f (3) = f (2 + 1) ≈ f (2) + f '(2) . 1= f (2) + (4) 1 = f (2) + 4.

It is now time to use the previous estimate of f(2) since we have no better idea of what f(2) might be. Thus f (3) ≈ 4 + 4 = 8.

Interpretations: [graphical] The graphical idea of this technique is illustrated in Figure 1. The line with slope 1 through the point (1,3) gives us the estimate for f (2). Now at the point (2,4) we use the line with slope 4 to obtain the estimate for f(3), at the point (3,8). You can think of this process as going for a walk in the field of tangents determined by this differential equation. We start the trip at the point (1,3) and proceed along the line with slope determined by the differential equation until we come to the point (2,4). Now we use the differential equation at (2,4) to determine the slope of the next line and proceed on that line 'til we come to the point (3,8) where we end our short trip. Instead of walking on the solution curve, we have been travelling for short segments on lines that might be tangents to a solution. Note that we could readjust our lines more frequently thereby taking shorter trips on each segment before reevaluating the slope. Then we would find our path was closer to the solution's graph.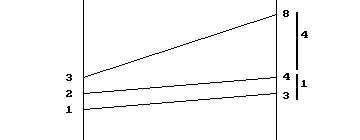

[Motion] The dynamic interpretation of our example is similar. See Figure.2. At time 1 second an object is 3 meters from a point P and its distance from P is increasing at a rate of 1(m/sec). We estimate its position at time 2 to be 4 due to the estimated change in position of 1 meter for the one second of time that has elapsed. Now we find at time 2 seconds that its rate is 4 (m/sec), so we estimate its position at time 3 seconds to be increased 4 meters for the next second of time, giving an estimate for the position at 3 seconds of being 8 meters from P.

[Cost] The economic interpretation of our example is similar. See Figure 2 again. When producing one unit of a product we'll suppose the cost is 3 dollars and its cost is increasing at a rate of 1(dollar/unit). Thus we estimate its total cost for 2 units to be 4 dollars due to the estimated cost of 1 dollar for the additional unit produced. Now we find that at 2 units of production the marginal cost is 4 (dollars/unit), so we estimate the total cost for 3 units of product to be 4 dollars for the next unit produced, giving an estimate for the total cost of producing 3 units as 8 dollars.

Comparison with The Exact Solution: Notice that in using this method the errors of approximation are compounded as we make approximations based on approximations. The exact solution of this differential equation is found easily since $\int x^2 dx = 1/3 x^3 + C$.

Because $3 = f (1) = 1/3 (1)^3 + C$ we have that $C = 8/3$. Thus $f (2) = 1/3(2^3) + 8/3 = 16/3 ≈ 5.333$ and $f (3) = 1/3(3^3) + 8/3 = 35/3 ≈ 11.667$ .

In each case we underestimated the precise value. Can you explain why we should have expected an underestimate from the nature of f '(x)? [Hint: What about the concavity of the graphical interpretation of a solution? What can you say about the acceleration in the dynamic interpretation of a solution?]

If we choose a smaller h at each step, the approximation will be better, but then we will need to process more steps to arrive at an estimate for f(2).
Here are the details with $dx = h = .1$ for estimating f (1.5). [From our exact solution, f (1.5)= (1.5) 3 /3 + 8/3 = 91/24 ≈ 3.7916667]. You can complete this example to estimate f (2) and f (3) yourself.
Table 1 shows one way to organize the information to estimate $f(2)$. Table 2 shows  a GeoGebra spreadsheet (downloadable) for the computations using $dx =h= 0.1$ through to $x=3$ and beyond.
[Here is a link for a spreadsheet you can use to complete this example yourself.]

a ≈ f(a) $f'(a)=a^2$
 $f'(a) \cdot h$
 Computation for f (a + h)
1 3 1 0.1 f (1.1) ≈f (1) + f '(1) . h
= 3 + (1) 2 .1 = 3.1 
1.1 3.1 1.21 0.121 f (1.2) ≈f (1.1) + f '(1.1) . h 
≈ 3.1 + (1.1) 2.1 = 3.221 
1.2 3.221 1.44 0.144 f (1.3) ≈f (1.2) + f '(1.2) . h
≈ 3.221 + (1.2) 2.1 = 3.365
1.3 3.365 1.69 0.169 f (1.4) ≈f (1.3) + f '(1.3) . h 
≈ 3.365 + (1.3) 2.1 = 3.534 
1.4 3.534 1.96 0.196 f (1.5) ≈f (1.4) + f '(1.4) . h 
≈ 3.534 + (1.4) 2.1 = 3.730 
1.5 3.73 2.25 0.225  
1.6 3.955 2.56 0.256  
1.7 4.211 2.89 0.289  
1.8 4.5 3.24 0.324  
1.9 4.824 3.61 0.361  
2 5.185      
Table 1
Table 2

Euler's Method: What is the generalization of this method? It is called Euler's method. As it is described below, keep in mind the examples we have just completed.

Step 1. First, suppose that we are given f (x 0) = y 0 and we want to estimate a solution to the differential equation f '(x) = P(x,y) where P(x,y) indicates a number that depends (possibly) on both the values of x and y. [In other words P(x,y) is a function of the two variables x and y. You might think of x as time and y as position in the dynamic interpretation so that we have a context where the velocity is determined by time and position. In the economic interpretation you might think of x as units of production and as y the total cost of production so that we have the marginal cost determined by level of production and current total cost.]

Step 2. We choose a value for h = dx and then let x 1 = x 0 + h.

Step 3. Now we estimate f (x 1) by y 1= y 0 + P(x 0 , y 0) . h.

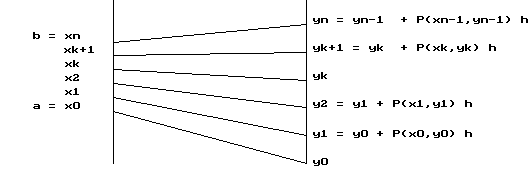
We continue by letting x 2 = x 1 + h [= x 0 + 2h] and estimate f (x 2) by y2 = y1 + P(x1,y1) . h.

In general (see Figure IV.E.4) we let

x k+1 = x k + h [= x 0 + (k+1) h]

and estimate f (x k+1) by

y k+1 = y k + P(x k , y k) . h.

If x 0 = a and x n = b then we have that f (b) is estimated by y n found after n applications of this method.
Since $b = x_n= x_0 + n*h = a + n*h$, if we wish to use this method to estimate f (b) starting from f (a) in n steps of equal length, then we use $h = (b-a)/n$. 

Here is another example to help you understand this further.

Example IV.E.2. Suppose f (1) = 5 and dy/dx = y - x. Estimate f (3) in 4 steps using Euler's method.

Solution: Linking this example to the notation of the previous discussion, we have

a = 1, b = 3, y 0 = 5 , P(x,y) = y - x, and n = 4.

So we set $dx = h = (b - a)/n = (3 - 1) /4 = 1/2 $. Table 2 summarizes the computations for y 1 through y 4 which will be the estimate for f(3). Keep in mind that y k+1 = y k + P(x k,y k) . h.

Thus we estimate the value of f (3) with y 4 = 19.1875 .  
Euler's Method

k
 x k
 y k
 P(x k,y k) = y k-x  k
 P(x k,y k).h 
0 1 5 4 2
1 1.5 7 5.5 2.75
2 2 9.75 7.75 3.875
3 2.5 13.625 11.125 5.5625
4 3 19.1875    
Table 3
Table 4 using GeoGebra

Using Sage to do this: Click on the Evaluate button.
You can change the derivative, $P(x,y)$, the initial values, $f(a) = c$, the differential, $dx=h$ , and $b=x_n$ , to estimate $f(b)$ using Euler's Method.

 

Note: As with our previous estimation based on the differential, if greater precision is desired in the estimate we should use a larger number of steps, and accordingly the value of $dx=h$ would be smaller. With even a relatively small number of steps (about 15 or 20) the computation required by Euler's method can become a rather mind dulling experience.

Here is an opportunity for a programmable calculator, computer program or spreadsheet to demonstrate its labor saving power as well as the power of Euler's method. To give a fairly accurate estimate of the value of f (b) you will want to work with a large number of steps.
Here is a downloadable GeoGebra applet showing spreadsheets, mapping diagrams, and tangent (slope) fields together to illustrate some of the power that Euler's method contributes to making sense of estimating solutions to an initial value problem.

[You can also use a spreadsheet which can be downlowded here.]
We'll discuss the accuracy of Euler's method for some cases in the next section.
Appendix IV.Y has two sample programs written in BASIC that illustrate the simplicity of Euler's method and how easily the method's algorithm can be translated into computer instructions.

Problems IV.E

For the differential equations in problems 1-4, assume y(1) = 2. (a) Estimate the value of y(3) using Euler's method with n = 4. Solve the differential equation algebraically and graph the solution.
Check your results with Sage or GeoGebra. [Remember that $dx = h = (b - a)/n$.]

(b) Draw a graph of the lines in the tangent plane used in Euler's estimation. Compare the estimate with the exact solution. Based on the concavity of the graph explain the quality of the error in your estimate.

(c) Draw a mapping figure that illustrates the dynamic or the economic interpretations  of Euler's method for your work. Discuss the interpretation of y'' and how it affects the quality of your estimates.
 
1. y' = .2 x 3 2. y' = x - 1
3. dy/dx = .5 x  4. dy/dx = .5 x 2 + 1
For the differential equations in problems 5 - 18 assume that y(1) = 2 and estimate the value of y(3) using Euler's method (a) when n = 4 ; (b) when n = 8; (c) check your results with Sage or GeoGebra, then (d) using computer software, a programmable calculator, or a spreadsheet  do the estimation when n = 100. State (if possible) whether your estimate is an underestimate or an overestimate and reasons for your conclusion.
 
5. y' = 1/x  $x \ne 0$ 6. y' = 1/(1+x)  $x\ne-1$
7. y' = 1/(x 2+1) 8. y' = x/(x 2 + 1)
9. dy/dt = 2y 10. dy/dt = -y
11. y' = -2y + x 12. y' = -2x + y
13. y' = 1/y     $y \ne 0$ 14. y' = 2/(1+y)   $y\ne-1$
15. dy/dx = x 2 + y 2 16. dy/dt = 1 /(t 2 + y 2)
17. y' = -x/y     $y \ne 0$ 18. y' = -y/x      $x \ne 0$

  1.  Calculate by hand, by Sage or GeoGebra, or by some other software the approximate value of a solution at x = 1 to the differential equation y'= x 2 + 1 with y(0) = 1 , i.e. , approximate y(1), using Euler's method with the following values of n: a) n = 4 ; b) n = 10 ; c) n = 100. Compare your estimate with the solution's actual value. Do you see any relation between the size of n and the size of the difference between your estimate and the actual value?
  2. Repeat problem 19 for the differential equation dy/dt = y .
  3. Note that if y = x 1/2 then y 2= x and for y not equal to 0, y'= 1/(2y). Use Euler's method with n = 20 to approximate 5 1/2 from 4 1/2 = 2.

    4. Hint: y(4) = 2 for the relevant solution to the differential equation.]
    State (if possible) whether your estimate is an underestimate or an overestimate and reasons for your conclusion.
  4. (a) For the situation in problem 10(a) of IV.A assume that k = 1. Use Euler's method with n = 4 to estimate the runner's distance from the finish line when one second before the end of the race.

    5. (b) For the situation in problem 10(b) of IV.A assume that k = 1. Use Euler's method with n = 10 to estimate the biomass of the cells when t = 1. (c) For the situation in problem 10(c) of IV.A assume that k = 1. Use Euler's method with n=10 to estimate the temperature of the coffee when t = 10.

    Euler's method can be extended and generalized in many ways. In problems 22-28 we explore extending it to estimate solutions to second order differential equations.

  5. Suppose $y'' = x - 3 , y'(0) = 2$ and $y(0) = 5$. [Ans]
    1. Using the differential of $y$, estimate $y(1)$.
    2. Using the differential of $y'$, estimate $y'(1)$. [Hint : $f '(a + h) ≈ f '(a) + f ''(a) . h$ is the relevant formula.]
    3. Using a) and b) and the differential , estimate $y(2)$.
    4. Estimate $y'(2$) and use this to estimate $y(3)$.
    5. Estimate $y(4)$.
  6. Suppose y'' = y , y'(0) = 2 and y(0) = 5.
    1. Using the differential of y estimate y(1).
    2. Using the differential of y' estimate y'(1).
    3. Using a) and b) and the differential , estimate y(2).
    4. Estimate y'(2),use this to estimate y(3), and then estimate y(4).
  7. Suppose y'' = -y , y'(0) = 1 and y(0) = 0.  [Ans] Using the ideas of problems 22 and 23, estimate y(1), y(2), y(3), and y(4).

    8. 26-28. Problems 23-25 used 4 steps to estimate y(4). Use the same ideas to estimate the solution to those problems with 8 steps.

29. Write and run a computer program that will estimate the solution to problem 25 in 40 steps, 400 steps and 4000 steps. A solution to this differential equation is y = sin(x). Compare the results of running your programs to the value for sin(4) on your calculator.