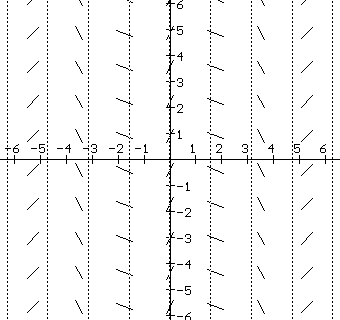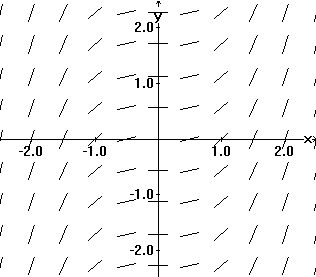
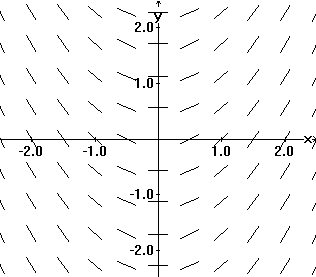
A tangent field determined by y' = x2 |
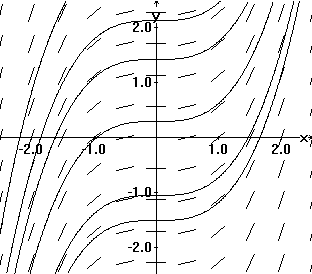
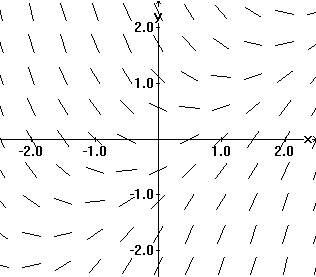
Solution curves drawn in a tangent field determined by y' = x2 |

A tangent field determined by y' = x2 |

Solution curves drawn in a tangent field determined by y' = x2 |
But first let's think of drawing the graph of a solution to the differential equation in the tangent field. Any tangents to a solution should have slopes close to the slopes of nearby segments already drawn in the tangent field. In this sense we can say that the shape of the graph of a solution fits consistently with the line segments of the tangent field. This property gives a method for sketching a solution's graph in a tangent field. Make the solution curve's sketch fit with the segments as well as possible. It's very much like the situation of children asked to connect dots to discover a picture. The instruction now is to draw a curve starting at some point (perhaps based on some initial condition) so that if the curve passes through or near one of the line segments in the field, the tangent to the curve should have a slope close to that of the line segment of the field.
Integral Curves: Since the curves drawn in the tangent field assemble information from the differential equation and represent solutions to the differential equation, they are called integral curves. Notice that the integral curves determined by a differential equation of the form y' = dy/dx = P(x) help visualize the indefinite integral `int` P(x) dx. The graphs represent members of the solution family by their graphs.
EXAMPLE IV.D.1: Draw segments of the tangent lines at various points for the differential equation dy/dx = x 2, that is, draw a tangent field for dy/dx = x 2.
DISCUSSION:
|

|

|
To repeat the idea here, at selected points in the plane the tangent field has a line segment with its slope determined by the differential equation.
Now consider Figure IV.D.iii. This is a graph of some integral curves for the differential equation dy/dx = x 2. They are the graphs of y = (1/3) x 3 + C determined by a few values of C. These curves are parallel in the sense that the difference between Y values of any two of these curves is a constant. This is consistent with the geometric interpretation of Theorem 4.2. [The optical illusion that the curves are further apart at the center of the figure and closer at the left or right sides of this figure is a result of the tendency of the eye to relate these curves by their closest points instead of vertically.]
More examples may help you understand the concept of a tangent field and the visualization of integral curves-- so consider these:
EXAMPLE IV.D.2. Graph the tangent field for y'= 0 .
Solution:
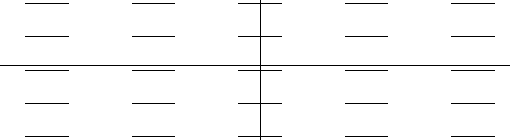
|
EXAMPLE IV.D.3. Graph the tangent field for y' = x .
Solution:
|
Discussion: Here again the tangent field graph in Figure IV.D.v suggests the graphs of the solution integral curves will form a family of parallel curves. It is fairly easy to draw tangent fields where the derivative depends only on the first coordinate variable, x. For x = a, you need only compute dy/dx at that value of x from the differential equation. Then you can draw in the figure numerous line segments with slope dy/dx along the vertical line X = a.
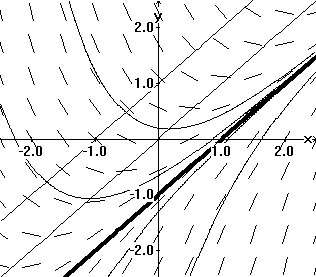
EXAMPLE IV.D.4. Graph the tangent field for y' = x - y . Describe the graph of the solution where y(0) = -1
Discussion: Here the problem is more subtle because the derivative depends on both coordinates of the point. For example, at the point (-1,2) we have that y' = -1 - 2 = -3 while at (0, -1) we find that y' = 0 - -1 = 1. A first approach to this tangent field is to select several points on the plane and compute y'. Figure IV.D.vi(a) shows an efficient way to display this information in a table.
|
|
|
After this kind of detailed work you may have noticed that for all points
on the line y = x, the value of y' is 0 . This can be seen
easily by noticing that y' = 0 implies that 0 = x - y. Similar
analysis shows that y' = 1 when 1 = x - y, that is along
the line y = x - 1.In general the same analysis shows that
y'
= m when m = x - y, that is along the line y = x - m. This
allows a more complete picture of the tangent field as drawn in Figure
IV.D.v(c). Notice that this figure suggests two essentially different types
of integral curves separated by the line y = x - 1. In fact
the line y = x - 1 is also an integral curve for this differential
equation since for any point on this line, 1 = y' = x - y.
Thus the solution with y(0) = -1 is given by this special solution
y = x - 1.
An On-line Direction Field Java Applet. Here's a tool for drawing
some simple tangent fields. Though this Java Applet draws arrows (vectors)
instead of line segments, you can see pretty clearly how it works. [For
more information, use the help button on the web page.]
Visualizing
Vector [tangent] Fields and First Order [Ordinary] Differential Equations
(by
Eugene Serdiouk.)
In problems 1-20, for each given differential equations (a) sketch the
tangent field showing tangents in all four quadrants. (b) Draw three integral
curves on your sketch including one through the point (1,2); (c)
Suppose that a solution to the differential equation has value
2 at 1. Based on your graph, estimate the value of that solution
at 2 and at 4. If the values of the solution are too large for x = 2
or x=4 to be estimated from your graph, discuss briefly why this is happenning
based on your sketch.
| 1. y' = x 3 | 2. y' = x - 1 |
| 3. f '(x) = .5 x | 4. dy/dx = 1 - x |
| 5. L'(t) = 1/t ... t `!=` 0 | 6. L'(t)= 1/(1+t) ... t `!=`-1 |
| 7. DP(t) = 1/(t 2+1) | 8. dz/dx = x/(x 2 + 1) |
| 9. y' = 2y | 10. y' = -y |
| 11. dy/dx = -2y + x | 12. dy/dt = -2t + y |
| 13. y' = 1/y ... y `!=` 0 | 14. z' = 2/(1+z) ... z `!=`-1 |
| 15. y' = y 2 | 16. P'(t) = t 2 + (P(t)) 2 |
| 17. dy/dx = -x/y y `!=` 0 | 18. dy/dx = -y/x |
| 19. dy/dt = 1/t 2 ... t `!=` 0 | 20. y' = 1 /(x 2+y 2)...(x,y) `!=` (0,0) |
For each of the following indefinite integrals use the tangent field
to sketch the graph of three indefinite integrals. Discuss the general
features of this graph based on whatever else you can gather from the integrand.
| a) `int` 3x
2 - 2x + 1 |
b) `int t sqrt(1+t^2)dt` |
| c) `int` sin(x) cos(x) dx | d) `int` (1- x2 )-1 dx |
| e) `int` sin(x 2) dx | f) `int` exp (-x 2) dx |
a) y'= x 2 - y2
b) y'= |x|.5
c) y'= y - x
d) yy'= 1 ..y` !=` 0
e) y'= 1 - y
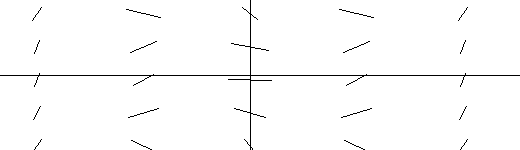 |
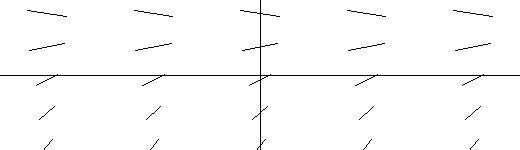 |
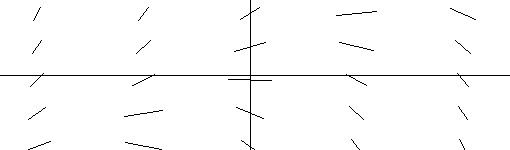 |
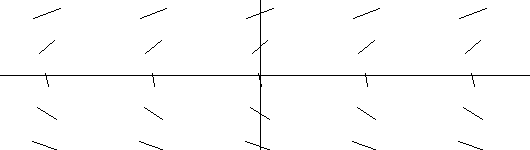 |