[The Dart Model] Suppose you are throwing a dart at a region in the plane and measuring a random variable X determined by the position of the dart. X has values only between 0 and 10. Unfortunately you are not given the distribution function of X. [Recall that for any real number A between 0 and 10 the distribution function F, would give you F(A), the probability that the value of X is less than or equal to A.] 
Instead you have been given a graph, an algebraic expression and a table for the probability density function of X. [Recall that  for any real number A between 0 and 10 the probability density function of X, f, gives you  f(A), the derivative of F at A, which is approximately the ratio of the probability of the random variable X being in an interval [A, A+h] to the length of that interval, h.] 
Based on this information do you think you could estimate the probability that the value of X being less 5? Recognizing that F(0) = 0 and F(10) = 1, could you estimate F(A) for any A between 0 and 10? As a practical matter, you might break the interval into10 pieces of equal length and then estimate the probability of X being in each of those interval from the density of X at some point in that interval. Then for A, just add up the probability estimates for X being in an interval that has values less than or equal to A. 
A f (A)
0.5 .05
1.5 .13
2.5 .11
3.5 .15
4.5 .19
5.5 .17
6.5 .09
7.5 .07
8.5 .03
9.5 .01
 
Graph of data for f(A) 
The Probability Density Function for X

Solution: As suggested, consider the interval [0,10] broken into smaller intervals each of length 1, i.e., [0,1], [1,2], [2,3], ... , [8,9], and [9,10]. Since each of these intervals has length 1, we can use f (A) as an estimate for the probability of the dart falling in the inteval that contains A. So, for example we estimate the probability that X lies in the interval [0,1] with f (.5) = .05, while we estimate the probability that X lies in the interval [1,2] with f (1.5) = .13. Continuing in this fashion we make estimates of the probability of X being in each of the ten intervals. 

Now use these to estimate the probability that X is less than 5 by accumulating the probabilities of the intervals that would have X less than 5. Thus we estimate 

F(5) = Prob( X<5) = 0.05 + 0.13 +  0.11 + 0.15 + 0.19 = 0.64 .
The distribution function might be estimated by assuming the density is uniform for each of the ten intervals. So, for example, if 0<A<1 then F(A) = 0.05 A, while if 1<A<2 then F(A) = 0.05 + 0.13(A-1). Following this pattern if 9<A<10 then F(A) = 0.99 + .01(A-9). 
 

One way to visualize this example is to use the density function value for the height of a rectangle with a unit base. Then the region in the plane above the interval [0,10} has a total area of one square unit. Assuming the distribution is uniform for each interval allows us to see the probability that X < A as the area of the region above the X axis and bounded by the vertical lines, X = 0 and X = A. 
Estimated probabilities that X is in an interval based on the given probability densities
interval Estimated probability 
[0,1]
.05
[1,2]
.13
[2,3]
.11
[3,4]
.15
[4,5]
.19
[5,6]
.17
[6,7]
.09
[7,8]
.07
[8,9]
.03
[9,10]
.01

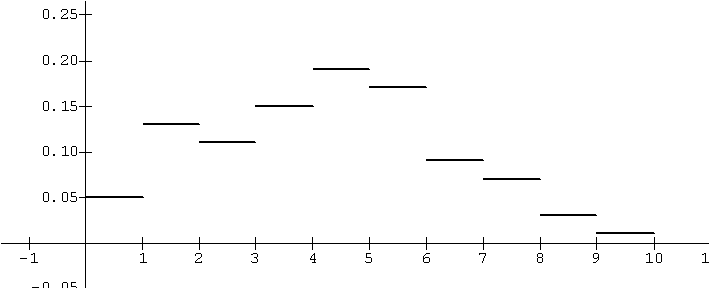
Estimated probability distribution function based on the given probability densities
A in the interval
F(A) 
[0,1]
.05 A
[1,2]
.05 +.13 (A - 1)
[2,3]
0.18 + .11 (A - 2)
[3,4]
0.29 + .15 (A - 3)
[4,5]
0.44 + .19 (A - 4)
[5,6]
0.63 + .17 (A - 5)
[6,7]
0.80 + .09 (A - 6)
[7,8]
0.89 + .07 (A - 7)
[8,9]
0.96 + .03 (A - 8)
[9,10]
0.99 + .01 (A - 9)
 
Graph of Estimated 
Probability Distribution Function for X 
based on the given probability densities