CHAPTER III Applications of the Derivative (Draft- 2014 work in progress)
$\textcopyright$ 2014 M. Flashman
Introduction:
As we saw in Chapters I and II, the derivative can be a powerful
analytic tool for any quantifiable scientific discipline. In many
interpretations this concept consolidates information about changing
relations between variables.
The symbolic and
numeric methods for finding or estimating the derivative as a number or
as a function make it efficient, eliminating repetitive arguments and
computations, and allow the focus of its use to remain on the
applications, keeping most mathematical manipulations routine and
secondary.
The visual tools of graphs and mapping diagrams provide additional
power to the concept by supplying alternative meanings for more
abstract contexts. Applications of the derivative are not limited to
those previewed in chapter I or to those that we will discuss in this
chapter. In fact one could easily describe everything in this text as an
application of the derivative in some fashion!
We will analyze three types of applications in this section. Each has a
wide scope of impact extending well beyond the specific context in which
we will see them initially.
A. Estimations:
Understanding estimations is a critical part of any science that uses
measurements. The key in using the derivative to estimate values
lies in the assumption that a function with a derivative behaves like a
function with a constant rate of change for some small interval. In this
chapter we will use the derivative in two common estimation procedures.
First, we will estimate the value of a function thinking of it as a
position function in a motion interpretation. Then we will discuss
an algorithmic process called Newton's method to estimate a zero of a
function or root of an equation thinking of this number as a time when a
position function is at the initial distance or graphically as the
X-intercept coordinate of a curve.
B. Graphs: The important role played by graphs in current science is
undeniable. It is the chief tool of visualization of data and provides
an efficient vehicle for suggesting relations between variables. With
the power that technology adds to the creation and display of graphs,
the need for better understanding of graphical features and their
analysis has risen while the need to analyze functions represented
symbolically for quick and accurate drawings has diminished only
slightly. As we saw in Chapter I, an understanding of the derivative can
bring with it a richer appreciation for graphic function properties.
C. Modeling: It is in the sciences that the use of the
derivative as a mathematical concept pays for the time and effort it
takes to master its notation and rules. Without the ability to bring
this abstraction into more then just the problems generated by
mathematics alone, it would be hard to see why mathematics would be as
prominent as the "language of science." Even with the rise of
computational power through technology, the use of the derivative
continues as before to describe and investigate the world through the measurement of variables.
In the next chapter we will look more extensively at the
ramifications of describing a context by relating the rates at which
variables change.
In this chapter we will look at models where the relation between the variables can be expressed in some equation or with a function with one controlling variable. Though
this may seem limited in scope, the questions we will examine for these
models are of sufficient generality to make them good prototypes for more general models.
The questions are simply how to use the information available to predict the
behavior of variables under specific constraints. Just as with the
graphical applications, the derivative can inform us of extremes,
intervals where variables will increase and decrease, even the rates at
which the rates of change change.
III.A. ESTIMATIONS USING THE DERIVATIVE
III.A.1. THE DIFFERENTIAL
MOTIVATION:
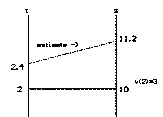
Consider a jogger running on a straight track so that after 2 seconds
the jogger is 10 meters from the starting point P and at that moment is
moving away from P with a velocity of 3 meters/sec. I would like
to approximate the position of the jogger 0.4 seconds later.
It seems
reasonable to assume for this estimation that the velocity wouldn't change
much in .4 of a second. So we'll treat the velocity of the jogger as a
constant.
Now it should be apparent that in 0.4 of a second the jogger would
move approximately (.4)(3) meters further away from P so that the jogger
would be approximately 10 + 1.2 = 11.2 meters from P.
We can express this
analysis more technically using some function notation. Let $t$ denote the
time in seconds and $s(t)$ denote the jogger's distance from $P$ at time $t$.
Then the initial facts were that $s(2) = 10$ and that $s'(2)=3$.
To estimate
the change in the value of $s$ for $0.4$ seconds we multiplied $s'(2)$, the rate
at which the jogger was running, by $0.4,$ the time the jogger would be running.
In symbolic form we had $s(2.4)-s(2) \approx
s'(2) .4 = 3 (.4) = 1.2$.
Now we complete the analysis by adding the
estimate of the change to the runners position at $2$ seconds giving
$s(2.4) = s(2) + {s(2.4) - s(2)}\approx 10 +
1.2 = 11.2$.
The simple technique
we used here generalizes to a method for estimating values
of any differentiable function based on information about the value of
the function and its derivative at a single point. The key is using the
product of the value of the derivative with a small change in the controlling
variable to estimate the change in the corresponding change in the function's
value.
The word that has been used since Leibniz to describe the estimate
for the change is the "differential."
|
 |
Definition and Notation: Suppose $f$ is a function that
is differentiable at $a$ and $h$ is any real number. We'll write
$df = df(a,h) = f '(a ) \cdot h$
.
df is
called "the differential of f at a." As the more complete notation
df (a,h) suggests, the quantity
df depends
on both the numbers a and h. When the notation
y =
f (
x)
is used to describe the function, then we also denote the differential
with
dy as well as
df.
Interpretation:
We can interpret the number a as a time at which we know information about
the value of
f. The number h can be thought of as measuring a time
interval we add to (or subtract from) a to determine a later (or earlier)
time at which we would like to know the function's value. The value of
d
f is then an estimate of the change in the function's value at
this later (or earlier) time, $a+h$. Thus $df(a,h) \approx
f(a+h) - f(a)$.
It is important to distinguish $df$ from $Df$. The notations
are very close so keep in mind:
- $df$ is the differential of f which gives an estimated change
in the value of the function $f$,
- $Df$ is the derivative of $f$ which gives the rate of change of $f$.
REMARK: We
can apply this new notation to the motivating example to focus its use
more sharply. Recall that s is the distance function for the jogger which
depends on the time variable $t$. The differential of $s$ at $2$ is therefore
given by $ds = ds(2,h) = s'(2) h = 3
h \approx s(2+h) - s(2)$. Now
using $s(2) = 10$ and $s'(2) = 3$, we have $s(2 + h) \approx
s( 2) + ds = 10 + 3h$ for any $h$, and when $h = .4$ we have $s(2.4) \approx
11.2$. Of course, in the jogger situation, the closeness of this estimate
depends on how the runner's velocity, $s'(t)$, actually varies between $2$
and $2.4$ seconds. It should seem reasonable to suppose that since $.4$ is
close to $0$, the estimate is fairly accurate and that it would be more accurate
for choices of $h$ even closer to $0$.
More on notation: The notation of the differential was introduced
by Leibniz with a different view of what it represented from its
current use. In particular Leibniz used the symbols dy and dt
to represent the measures of very small- I mean extremely small- segments
measuring the rise and run of very short sections of a curve. Thus it appears
that Leibniz was interested in finding the slope of a curve by inspecting
the curve very closely. This is analogous to what we might do today with
the ability to zoom in with graphical technology so that the graph of a
curve would appear to be indistinguishable from the graph of a line. We
will continue in this section to develop the notation for differentials
to allow us to make some sense out of this older view. The Leibniz notation
has proved particularly successful in connecting many concepts to scientific
applications.
What does $dx$
denote? Suppose $x(t) = t$ for all $t$. Then $dx=
dx(a,h) = x'(a) \cdot h$. But $x'(t)
= 1$ for all $t$, so $dx= h$. This bizzare consequence of the
notation justifies the abuse of notation in saying that when $y =
f (x)$,
$dy = df = f '(a) \cdot h = f
'(a) \cdot dx$ .
It is possible now
to make sense in many situations of Leibniz notation even though the original
use of this notation most likely had a very different though consistent
meaning to Leibniz and others historically. For example, with
this notation $ \frac {df}{dx}$ and $\frac {dy}{dx}$ can be interpreted
as quotients so that
$ \frac {df}{dx} =\frac {dy}{dx} = \frac{f '(a) dx}{dx} = f
'(a)$.
More Notation:
In Chapter I we used $h$ for some of our initial derivative estimations.
We suppose again that $y= f(x)$ and let
$\Delta x = h$ and $\Delta y
= \Delta y(a,h) = f(a+h) - f(a)$.
By our previous comments
then $dx
= \Delta x = h$ and $\Delta y
= f(a+dx)- f(a)$.
|
| Comment on notation. In most American mathematics books the
notation for the change in a variable's value uses the Greek letter upper
case delta, $\Delta$ such as $\Delta x$ for change in the
variable $x$ and $\Delta t$ for change in the variable
t. In some physics books and British mathematics books the lower case of
the same letter, $\delta$, appears, so you might see in $\delta x$
or $\delta t$. For some users of these notation a minor
distinction might be made in the use...$\Delta x$ would
be used for any change in the variable $x$, whereas $\delta x$
would indicate that there was a very small change in the variable $x$...so
small that it would be almost imperceptible. |
|
Estimates with the differential: The heart of the matter in
making an estimate of
f(a+h) with the differential is the fact that
for small values of h, dy \approx \Delta y,
so that
$f(a + dx) = f(a)+\Delta y \approx f(a) + dy = f(a)
+ f '(a) \cdot dx$.
EXAMPLE: (Let's try it.) Find $dy$ when $y = f(x) =
x^3 - 5x + 7$. Evaluate $dy$ when $x = 2$ and $dx = 0.3$. Use $dy$
to estimate $y$ when $x = 2.3$. Find $f(2.3)$ and $\Delta y$
exactly.
SOLUTION: Using
$y = f(x)$, we have that $f '(x) = 3x^2 - 5$ so $dy
= f '(a)dx = ( 3a^2 - 5 ) dx$.
To evaluate $dy$ we
merely replace $a$ with $2$ and $dx$ with $0.3$ in the expression to
obtain
$dy = ( 3(2)^2 - 5 ) (.3) = 2.1$
Noticing that $f(2)
= (8 - 10 + 7)= 5$, we estimate
$f(2.3) = f(2 + .3) \approx
f(2) + dy = 5 + 2.1 = 7.1$.
It is not hard to find $f(2.3) =(2.3)^3 - 5(2.3) +
7 = 7.667$, so that $\Delta y = 7.667 -5 = 2.667$.
It is worth noting here that the size of the error in the differential
estimate of $f(2.3)$ is the difference between
$7.667-7.1 = f(2.3) - (f(2) + dy) = \Delta y
- dy = 2.667 - 2.1 = .567$.
We can compare this error in estimating the difference in values as a percent
of the size of the precise difference $\Delta y$ to
find the percent of relative error in this estimate is $0.567/2.667
= .2126 = 21.26\%$.
EXAMPLES:To see the relative quality of the estimate
for values of a function using the differential let's look at the sine
function values using the differential at 0. We compare these in Table
1 with the estimation values that arise from the differential. Since $\sin(0)=0$
and $\sin'(0)= \cos(0)=1$, the estimate for $\sin(0+h)$ is $\sin(0)+\sin'(0)\cdot h =
h$. So Table 1 demonstrates that when $h \approx
0, sin(h) \approx h$.
[This should remind you of the fact we demonstrated in chapter I, namely
that $\lim_{h \to 0} \frac {\sin(h)} h =1$.]
The errors in the estimates of this table are clearly smaller when
$h$ is closer to $0$.
[Can you see why we haven't considered relative errors here?] |
| $\sin(h)$
|
estimate
| |
0.1
|
9.9833416647e-02
|
0.1
| |
0.01
|
9.9998333342e-03
|
0.01
| |
0.001
|
9.9999983333e-04
|
0.001
| |
0.0001
|
9.9999999833e-05
|
0.0001
| |
0.00001
|
9.9999999998e-06
|
0.00001
| |
0.000001
|
1.0000000000e-06
|
0.000001
|
|
A similar comparison
for $f(x)=1/x$ using the differential at $1$ shows a less symmetric
situation. Here $f(1)= 1$ and $f '(1)= -1$ so $f(1+h)$ is
approximated by $f(1) + f '(1) \cdot h = 1 - h$. Table 2 shows how
these estimates compare with some function values close to $1$. Again the
errors in the estimates are smaller when $h$ is closer to $0$, as are the relative
errors which are shown as percentages in the table. |
Table 2
|
$h$
|
$a=1+h$
|
$1/a$
|
estimate
|
relative error
| |
0.5
|
1.5
|
0.6666667
|
0.5
|
33.33%
| |
0.1
|
1.1
|
0.9090909
|
0.9
|
9.09%
| |
0.01
|
1.01
|
0.990099
|
0.99
|
0.99%
| |
0.001
|
1.001
|
0.999001
|
0.999
|
0.10%
| |
-0.5
|
0.5
|
2
|
1.5
|
-100.00%
| |
-0.1
|
0.9
|
1.1111111
|
1.1
|
-11.11%
| |
-0.01
|
0.99
|
1.010101
|
1.01
|
-1.01%
| |
-0.001
|
0.999
|
1.001001
|
1.001
|
-0.10%
|
|
Interpretation
(Mapping Diagram): Assume $h =dx >0$. In the mapping diagram
below [Figure 2] we have labeled the lengths of the key elements determining
the differential, namely the points on the source line, $a$ and $a+dx$, and
the points on the target line:
f(a),
f(a+dx), and the estimate
based on the differential,
f(a) +
f '(a)
.dx. When
$h=dx$ is small we have that the average rate of change of the
f values
on the interval $[a,a+h]$ is a good estimate for the instantaneous rate of
change of
f at a,
f '(a). That is,
$ \frac {f(a+h)-f(a)} h =\frac {\Delta y}{\Delta x} \approx f'(a)$.
Thus $\Delta y = f(a+h)-f(a) \approx f'(a) \cdot h = df$.
By looking at the
target line we can see the estimating value compared to the precise value
of f(a+h). For the estimate, the length f(a) is increased
(decreased) by the length df. When h is closer to 0, the differential's
length will be closer to the length of the segment between f(a+h)
and f(a), so the estimation will be more accurate.
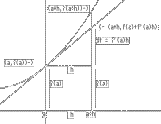
Interpretation
(The graph and the tangent line): The differential of $f$
at a can also be visualized using the interpretation of the derivative
as the slope of the line tangent to the graph of $y=f(x)$ at the point
$(a, f(a))$. Figure 2 shows the lengths of the key elements
used in determining the differential, namely the points on the graph of
$f$, $(a,f(a))$ and $(a+h,f(a+h))$, and on the tangent line
$(a+h, f(a)+f '(a) \cdot h)$.
Note that the second coordinate of the point on the tangent line was
determined from the fact that the slope is $f '(a)$. When $h$ is small
we have that the slope of the secant line determined by $(a,f(a))$
and $(a+h,f(a+h))$ is a good estimate for the slope of the tangent
line, $f '(a)$, i.e, $\frac {f(a+h)-f(a)} h =\frac {\Delta y}{\Delta x} \approx f'(a)$.
By multiplying both sides of this estimate by $h$ we find
yet another way to understand the estimate
$\Delta y = f(a+h)-f(a) \approx f'(a) \cdot h = df$.
|
 |
|
Notice how the points on the graph are paired with the arrows on the mapping diagram.
Martin Flashman, Oct 2014, Created with GeoGebra
|
We can examine the
figure in greater detail to see how the differential is used to estimate
$f(a+h)$. The vertical line segment used to measure $f(a+h)-f(a)
=\Delta y$
can be compared to the vertical segment of the right triangle formed by
the tangent line, the vertical line X = a+h and the horizontal line Y =
f(a). The base of this triangle has length $h=\Delta x=dx$.
Because the tangent line has slope f '(a) the segment on the
vertical line $X=a+h$ has must have l ength $f '(a) \cdot h
= dy$. Again we have a way to see that $dy/h = dy/dx=f '(a)$, the derivative
is the quotient of differentials! The estimation can be seen by thinking
of the point $(a+h, f(a+h))$ approximated by extending the vertical
segment of the line $X=a+h$ from the point $(a+h, f(a))$ by the length
$dy$.
Interpretation:
(Economics): Consider a function model for the cost C of producing x
kilograms of a perfectly divisible commodity. As we saw in chapter I, when
we produce a kilograms, the marginal cost is C'(a). If we
decide to produce an additional h kilograms of our product, we can estimate
the change in our costs and our new costs with the differential at a.
Thus $\Delta C \cdot
dC= dC(a,h) = C'(a) \cdot h$ and $C(a+h) \cdot C(a)
+ dC = C(a) + C'(a)\cdot
h$. [The marginal cost at $a$, which we denoted $MC(a)$ in chapter
I, originally meant the change in the cost for a change of one unit of
production. Now the $MC(a)$ can be connected more directly to the derivative
by using the differential estimation, giving $MC(a) \cdot
dC(a, 1)=C'(a)$.] See exercises.....
Interpretation:
(Probability). Consider a continuous random variable $X$ with a distribution
function $F$ defined on an interval $I$. The probability that $X$ is between
the values $A$ and $A+h$, $Pr(A<X<A+h)$, is given precisely by $F(A+h) -
F(A)$, the change in the distribution function values for the interval $[a.a+h]$.
Using the differential to estimate the change in the distribution function
values, we have that this probability is estimated by $dF(A,h)=F'(A)\cdot
h$. Now $F'(A)$ is interpreted as the point probability density of $X$ at the number $A$, which
is conventionally denoted by $f(A)$. Thus for small intervals, that
is, when $h$ is small, the probability that the random variable $X$ is
between $A$ and $A+h$ is approximately $f(A)\cdot
h$, the value of the density function for $X$ at $A$ times the length
of the interval. See exercises.
Application: A
hollow spherical steel ball has an inside radius of $2$ meters and a thickness
of $3$ centimeters. Estimate the volume and the mass of the steel in the
wall of the ball. Discuss the relative size of the error in using the differential
to make this estimate.[Assume the density of the steel is $1254$ kilograms
per cubic meter.]
Solution: Let
$V(r)$ denote the volume of a sphere of radius $r$. This problem asks for an
estimate of the volume of the steel in the wall of a sphere, which can
be expressed as $V(2.03) - V(2) =\Delta V$. The formula for the volume of a sphere says that $V(r)= 4/3 \pi
r^3$. Using $a = 2$ and $h = 0.03$ and the differential we have
$\Delta V \approx
dV = V'(a) \cdot h = 4 \pi a^2 \cdot h = 4 \pi 4(.03)
=.48 \pi$.
cubic meters.
Application: Use
the differential to estimate $9^ {1/3}$ from the fact that $8^{1/3}
= 2$.
Solution: Consider
$f(x) = x^{1/3}$. $f(9) = f(8+1)$ so in the notation
we've established we let $a=8$ and $h= dx =1$.
Thus $f(a+dx)\approx f(a)
+ f '(a) \cdot dx = f(8) + f '(8) \cdot 1 = 2 + (1/3)(8)^{-2/3}$ so
$f(9) \approx
2 + 1/12 = 25/12$.
Notice
that what made this solution possible was the ability to evaluate both
$f(8)$ and $f '(8)$. This ease of computation was what actually
led to the choice of $a = 8$.
Application: Use
the differential to estimate 98 1/2 .
Solution: Consider
$f(x) = x^ {1/2}$. $ f(98) = f(100 - 2)$ so in
the notation we've established we let $a=100$ and $h=dx =-2$. Thus
$f(a+h)
\approx f(a)
+ f '(a) \cdot h = f(100) + f '(100) \cdot (-2)
= 10 + 1/2(100) ^{-1/2}\cdot (-2)$
and
so $f(98) \approx 10 - 1/10 = 9.9 $.
Estimation of relative error.
The relative error of a value, $V$ in a computation is determined by
measuring the error, $\Delta V$, in the computation and comparing
that as a ratio with the computed value, i.e., $\frac {\Delta V}
V$.
To make an estimate of the relative error, it makes sense to use $ dV
\approx \Delta V$ when $V$ is a differentiable function of a controlling
variable.
Example: Suppose the side of a cube is measured to be 5 meters
with a possible error in the measurement of at most 1 centimeter = 0.01
meters. Estimate the relative error in using the measurement of the
length of the side to compute the volume of the cube.
Solution: Let $s=5$ be the measurement of the side of the
cube and $V = s^3$ be the volume of the cube, which gives us $V =
5^3 = 125$ cubic meters. The largest possible error is $\Delta s = ds =
.01$.
We use $dV$ to estimate the error, $\Delta V \approx dV = 3s^2 \cdot ds$, so we
find that $dV = 3 \cdot 5^2 \cdot 0.01 = 0.75$ so the relative error is
approximately $ \frac {dV} V = \frac {0.75}/{125} = 0.006 = 0.6\%$
The
calculus of differentials.
Since the differential of a function is directly related to the derivative
of the function, we can write formulas for a calculus of differentials
each of which can be justified by reference to the appropriate derivative
rule. For example, if $u$ and $v$ are both functions of $x$, then $d(u.v)=udv+vdu$.
This is justified by considering the derivative product rule $D_x(u.v)=uD_x(v)+vD_x(u)$.
Hence
$d(u \cdot v) = D_x(u\cdot v)dx = [uD_x(v)
+ vD_x(u)]dx = uD_x(v)dx + vD_x(u)dx$ $= udv + vdu$.
In
the exercises for this section you will find similar results for
the "differential calculus" which you are asked to justify.
Exercises
III.A:
For
each of the functions in problems 1-6 find (a) $f(1)$, (b) $f(1.2)$, (c)$\Delta y(1,0.2)$,
and (d) $df(1,0.2)$. Check you work with the GeoGebra
Applet.
1. $f(x) = x^2 + 3x$
2. $f(x) = 5x^2 - 3x$
3. $f(x) = x^3 + 3x$
4. $f(x) = 5x^3 - 3x$
5. $f(x) = x^3 + x$
6. $f(x) = 5x^3 - x$
For
each of the functions in problems 7-12 use the differential to estimate
the value of (a) $f(1.1)$ and (b) $f(.95)$ .Check you work with the GeoGebra Applet.
7. $f(x) = x^2 + 3x$
8. $f(x) = 5x^2 - 3x$
9. $f(x) = x^3 + 3x$
10. $f(x) = 5x^3 - 3x$
11. $f(x) = x^3 + x $
12. $f(x) = 5x^3 - x$
In
problems 13-20, use the differential to estimate the indicated value.Check you work with the GeoGebra Applet.
13.
$(82) ^{1/2}$ 14. $(63)^{1/2}$
15. $(127) ^{1/3} $
16.$(25)
^{1/3} $ 17. $\frac 1{103}$
18. $\frac 1{998} $ 19.
$(33)^{1/5}$ 20. $(29^{1/5}$
21.
Use the differential to give a formula for estimating $\sqrt{x} = x^{1/2}$
when
$x$ is close to (a) 100 (b) 25 (c) 81 and (d) $t$.
22.
Use the differential to give a formula for estimating $\sqrt[3]{x} = x^{1/3}$
when
$x$ is close to (a) 1000 (b) 125 (c) 27 and (d) $t$.
23.
A circle of radius 3 meters is painted red with a edge of 10 centimeters
painted blue. Use the differential to estimate the area of the region that
is painted blue.
24.
A spherical ball of radius 20 centimeters is coated with a shell of plastic
0.5 cm in thickness. Estimate the volume of plastic of the plastic shell.
25.
A closed cylindrical tin can has radius 4 cm. and height 6 cm. Estimate
the volume of the tin if the tin is 3 mm in thickness.
26.
A rectangular poster that is 2 feet by 3 feet has a border of red that
is 1/2 inch wide. Estimate the area of the border using the differential.
Find the exact area of the border.
Justify
the differential calculus formulae in problems 27-33. Assume
that $u$ and $v$ are differentiable functions of $x$.
27.
$d(au) = adu$ where $a$ is any real number.
28.
$d(u + v) = du + dv$.
29.
$d(1/v) = -dv/v^2$.
30.
$d(u/v) =[vdu - udv]/v^2$ .
31.
$d(\sin u) = \cos u du$.
32.
$d(\sec u) = \sec u \tan u du$.
33.
Suppose that $w=f(u)$ and $u=g(x)$ and $y = f(g(x))$. Prove $dy
= dw/du \cdot du$ when interpreted appropriately.
34.
Suppose $g$ is a differentiable function with $g(2)=5$ and $g'(2)=10$. Estimate
the following:
$
g(3) , g(1.5) , g(2.1)$ and $g(1.99)$.
35.
Suppose g is a differentiable function with $g(1)=2$ and $g(2)=4$. If $g'(1)=4$
and $g'(2)=2$ ,give two estimates for $g(1.5)$ using the differential. Discuss
briefly how these estimates relate to the true value of $g(1.5)$.
36.
Project: Suppose $L(x)$ is a differentiable function with $L(0)=1$ and
for every $x > -1, L'(x)= \frac 1{1+x}$.
a)
Estimate $L(1/4)$.
b)
Based on your estimate for $L(1/4)$, estimate $L(1/2)$.
c)
Continue. Use the estimate of $L(1/2)$ and then $L(3/4)$ to estimate $L(1)$.
d)
Based on this work, suggest a method to estimate $L(1)$ more accurately.
Explain with an example using your method.
37.
Project: Suppose $P(x)$ is a differentiable function with $P(0)=1$ and
for every $x$, $P'(x)=3\cdot P(x)$.
a)
Estimate $P(1/4)$.
b)
Based on your estimate for $P(1/4)$, estimate $P(1/2)$.
c)
Continue. Use the estimate of $P(1/2)$ and then $P(3/4)$ to estimate $P(1)$.
d)
Based on this work, suggest a method to estimate $P(1)$ more accurately.
Explain with an example using your method.

