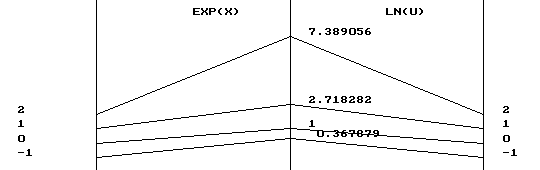
In the previous sections we have considered independently the functions that solved two differential equations. The "natural logarithm" function, ln , was the solution to the differential equation L'(t) = 1/t with L(1) = 0 , while the "natural exponential" function, exp or e, was the solution to the differential equation P'(t) = P(t) with P(0) = 1. You probably have seen these two functions before in your pre-calculus course work where they were closely related as the next theorem shows.
Theorem VI.C.1: (a) For all t > 0, exp(ln(t)) = t. (b) For all x, ln(exp(x)) = x.
Proof: (a) Let F(t) = exp(ln(t))/t for t > 0.
Then using the quotient and the chain rules we see that
F'(t) = [t .exp(ln(t)) .1/t - exp(ln(t)) .1]/t 2 = 0 for all t > 0.
Thus F(t) is a constant and since F(1)= exp(ln(1))/1 = exp(0)/1 = 1 we have
exp(ln(t))/t = 1 or exp(ln(t)) = t for all t > 0.
(b) Let F(x) = ln(exp(x)) - x for all x
.
Then using the chain rule we see that F'(x)= 1/exp(x)
.
exp(x)-1= 0 for all x .
Thus F(x) is a constant. Since F(0) = ln(exp(0)) - 0=
ln(1)= 0 we have ln(exp(x)) - x = 0 for all x or
ln(exp(x))
= x for all x .EOP

In functional terms, the composition of ln with exp is the identity function, as is also the composition of exp with ln, i.e.,
ln ° exp = id = exp ° ln,
when the domain is suitably chosen. For both these reasons we say
that
the natural logarithm and natural exponential function are inversely
related
as functions.
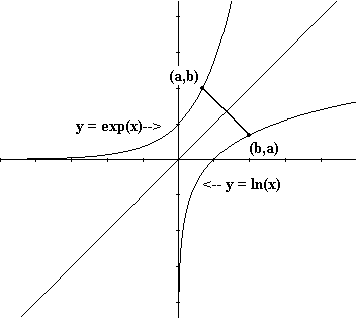 The cartesian
graphical way to view this inverse relation as in the GeoGebra figure is to note that if b =
exp(a)
then ln(b) = ln(exp(a)) = a . Thus if (a,b) is a point on the graph of
the natural exponential function, then (b,a) is a point on the graph of
the natural logarithm function. Similarly if a = ln(b) , b > 0 then
exp(a)
= exp(ln(b)) = b which shows that if (b,a) is a point on the graph of
the
natural logarithm function then (a,b) is a point on the graph of the
natural
exponential function. See Figure VI.C.ii. We summarize this by saying
exp(a)
= b if and only if b = ln(a) , or using the notation e a =
exp(a),
The cartesian
graphical way to view this inverse relation as in the GeoGebra figure is to note that if b =
exp(a)
then ln(b) = ln(exp(a)) = a . Thus if (a,b) is a point on the graph of
the natural exponential function, then (b,a) is a point on the graph of
the natural logarithm function. Similarly if a = ln(b) , b > 0 then
exp(a)
= exp(ln(b)) = b which shows that if (b,a) is a point on the graph of
the
natural logarithm function then (a,b) is a point on the graph of the
natural
exponential function. See Figure VI.C.ii. We summarize this by saying
exp(a)
= b if and only if b = ln(a) , or using the notation e a =
exp(a),
e a = b if and only if b = ln(a).
This last statement justifies calling the natural logarithm "the logarithm with the base e" and writing in more conventional terms ln(a) = log e(a). For example, e 0 = 1 so, ln(1) = 0 and e1=e so ln(e) = 1. In general ln(e a) = a , which merely restates part (b) of the theorem.
Applications: The inverse relation of these two functions is most convenient for finding ways to express the solutions to differential equations that are in exponential form as the following examples illustrate.
Example VI.C.1: Suppose f(x) = A e kx . Find A and k when f(0) = 20 and f(1) = 40. Find t so that f(t) = 100.
Solution: First we merely substitute the given values into the formula for f: 20 = f(0) = Ae k(0) = A so A=20, while 40=f(1)=A e k(1) =20 e k. So 2 = e k.
Using the inverse relation between ln and exp in this equation means precisely that k = ln(2). Thus f(x) = 20 e (ln(2) x).
To find when f(t) = 100 we need to solve 100 = 20 e (ln(2) t), or 5 = e (ln(2) t). Using the inverse properties once again, we have ln(5) = t ln(2) so
t = ln(5) / ln(2) » 2.32.
Example VI.C.2: Suppose f(x) = Ae kx and f(3) = 2f(0). If f(1) = 40, find f(5).
Solution: f(0) = A so we have been given 2 A = A e k3 in the statement f(3) = 2f(0). Thus 2 = e 3k , so by the inverse relation of ln and exp we have that 3k = ln(2) or k = (1/3) ln(2).
The second equation f(1) = 40 becomes 40 = Ae k. At this point we can solve for A theoretically by dividing both sides of the last equation by e k, giving A = 40 / e k. We continue with this form for A to find f(5) = A e k5 = (40 / e k) e 5k = 40 e 4k = 40 e 4/3 ln(2).
Recognizing this result is not the easiest number to compute, let's notice that
So f(5) = 40 (2) 4/3.
Find the first derivative for the functions in problems 1-4 using logarithmic differentiation:
Find the first derivative for the functions in problems 6-9.