|
|
|
|
|
1 |
|
|
0.69555501 |
|
|
0.6931712 |
|
|
0.69314742 |
|
|
0.69314718 |
|
|
0.69314776 |
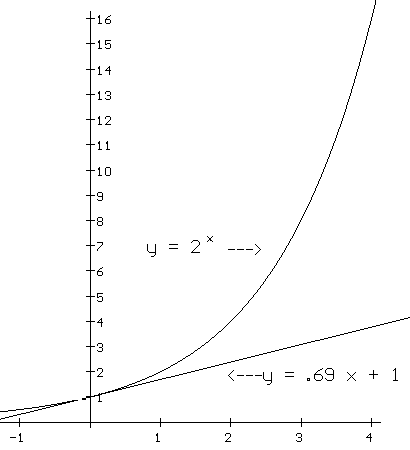
|
|
|
|
|
1 |
|
|
0.69555501 |
|
|
0.6931712 |
|
|
0.69314742 |
|
|
0.69314718 |
|
|
0.69314776 |
Let's start with f(x) = 2x and estimate
f '(0). Looking at the graph of this function in Figure *** certainly
supports the belief that f has a tangent line and thus that f
should have a derivative at 0. Consider the data in Table ***. It suggests
that ![]() .
.
| x | f(x)=2x |
|
|
| -4 | 0.0625 | 0.043322 | 0.6931495 |
| -3 | 0.125 | 0.086644 | 0.6931495 |
| -2 | 0.25 | 0.173287 | 0.6931495 |
| -1 | 0.5 | 0.346575 | 0.6931495 |
| 0 | 1 | 0.69315 | 0.6931496 |
| 1 | 2 | 1.386299 | 0.6931496 |
| 2 | 4 | 2.772598 | 0.6931496 |
| 3 | 8 | 5.545197 | 0.6931496 |
| 4 | 16 | 11.09039 | 0.6931496 |
Remarks: 1. This result does seem quite different from any we have had before because the derivative here is a constant multiple of the value of the function. In other words the derivative is proportional to the value of the function. We can check this is several ways to confirm the truth of the result.
First we can look at the ratio of a numerical estimate of the derivative at several points and see that even at the estimation level the ratio is constant. This is done in Figure *** using h=.0001 for the estimation. Another way to check the result is to draw lines using the function values times .693 for the slope at various points on the graph to see that these lines do appear to be tangent. Of course both these techniques do not fully justify the claim as does the analysis, but they do add to the credibility in making them sensible based on a variety of experiences.
Finally with technology you might match the graph of a numerical estimation of the derivative against the graph of .693 times 2x and notice how close these graphs appear.
2. The general exponential function with a base b ( not equal to 1) can be treated in the same fashion as the work we have done with the base 2. The result is that when f(x)=bx then f '(x)=f(x) f '(0). The argument to justify this is completely analogous to the argument we have just presented for the base 2.
Putting this together with the last statement we have that as h®0, ln(b)® ln(e)=1. But ln (b) is a constant. Therefore, ln (b) = 1 and it must be that b = e.
Our argument has shown that if there is a base b where the derivative of bx at 0 is 1, then that base must be the number e. By reversing the reasoning the converse statement can also be shown true. That is, we can justify the following core result:
If f(x) = ex then f '(0) = 1 and
therefore f '(x) = ex = f(x)
for any real number x.
|
|
|
| 1 | 1.718281828 |
| 0.1 | 1.051709181 |
| 0.01 | 1.005016708 |
| 0.001 | 1.000500167 |
| 0.0001 | 1.000050002 |
| 0.00001 | 1.000005 |
| x | |||
| -5 | 0.0067 | 0.006738 | 1.000005 |
| -4 | 0.0183 | 0.0183157 | 1.000005 |
| -3 | 0.0498 | 0.0497873 | 1.000005 |
| -2 | 0.1353 | 0.135336 | 1.000005 |
| -1 | 0.3679 | 0.3678813 | 1.000005 |
| 0 | 1 | 1.000005 | 1.000005 |
| 1 | 2.7183 | 2.7182954 | 1.000005 |
| 2 | 7.3891 | 7.389093 | 1.000005 |
| 3 | 20.086 | 20.085637 | 1.000005 |
| 4 | 54.598 | 54.598423 | 1.000005 |
| 5 | 148.41 | 148.4139 | 1.000005 |
Example. I.F.5. Find the derivative of ![]() .
.
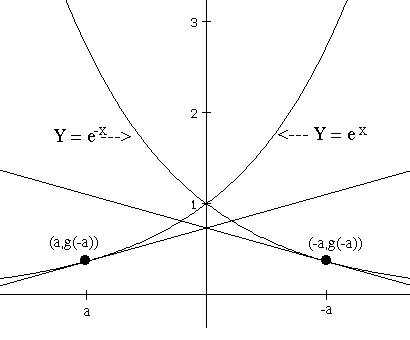
Solution: We will look at this from a graphical and an algebraic
viewpoint. From Figure *** as well as the simple algebra we can see that
g(-a)= e-(-a)= e a.
On the graph this result is seen in the fact that the graph of g(x) is the mirror image - reflection of the graph of e x. Considering the tangent line interpretation of the derivative, we see that the tangent line for the graph of g(x) at the point (-a, g(-a)) will be the mirror image - reflection of the tangent line to the graph of e x at the point (a, e a). The slope of this line is the derivative of e x at a, namely e a. The mirror image line will have the opposite slope, so the derivative of g at -a, g '(-a) = - e a. Now think of any number x as the opposite of a number, x=-a, so a=-x. Then the last statement says that g '(x) = g '(-a) = - e a =- e -x.
Here's another way to see this result using the symmetry of the graphs
and algebra: ![]() so g(x) is a simple exponential function with base
so g(x) is a simple exponential function with base ![]() . From the symmetry of the graphs of g(x) and e
x, the slope of the tangent line to the graph of g at (0,1)
is -1, so g '(0)= -1. See Figure *** Thus from the result we have
about derivative of simple exponential functions we have that
. From the symmetry of the graphs of g(x) and e
x, the slope of the tangent line to the graph of g at (0,1)
is -1, so g '(0)= -1. See Figure *** Thus from the result we have
about derivative of simple exponential functions we have that![]() .
.
The derivative of ln- the natural logarithm.
Here is a brief approach to finding the derivative of the natural
logarithm. Logarithmic functions with other bases may be done similarly.
The logarithmic functions will be treated again in Chapter II as well as
Chapter VI.
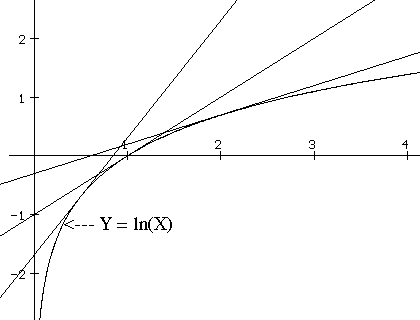
So suppose f (x) = ln(x) and we want to find f '(a). We
will use the difference quotient ![]() . The idea is simply to substitute y for f(x) and b
for f(a). The definition of the logarithm gives us that if
. The idea is simply to substitute y for f(x) and b
for f(a). The definition of the logarithm gives us that if ![]() then ey = x and similarly if
then ey = x and similarly if ![]() then e b = a. It should make sense from your experience
with logarithms that when x approaches a, y approaches
b. You should draw a transformation figure for ln(x) and ex
to help visualize these last statements.
then e b = a. It should make sense from your experience
with logarithms that when x approaches a, y approaches
b. You should draw a transformation figure for ln(x) and ex
to help visualize these last statements.
Now let's consider the difference quotient,
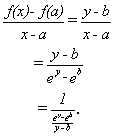 .
.Note: Notice how this result makes sense with the graphical interpretation. See Figure ***. When x is close to 0, the slope is quite large, while when x is large the slope of the tangent line slope seems closer to 0.
Derivatives of Other Logarithms: From your background (or the quick
review box)you may recall that if we know the natural logarithm of a number
x>0 and a base b>0 b¹1,then
the logarithm with the base b is determined by the equation ![]() . Applying the scalar multiple rule to this expression of the general logarithm
function with base b we have that
. Applying the scalar multiple rule to this expression of the general logarithm
function with base b we have that ![]() and
and ![]() .
.
Thus for example, ![]() .
.
Exercises I.F.2. In problems 1 to 3 find the indicated derivatives.