|
|
$\frac {2^h-1}h$ |
|
|
1 |
|
|
0.69555501 |
|
|
0.6931712 |
|
|
0.69314742 |
|
|
0.69314718 |
|
|
0.69314776 |
The Derivatives of Simple Exponential Functions. We begin with simple exponential functions. At this stage of our studies we will presume the variables in many models are controlled by an exponential function like $f(x) = 2^x$. In your prior work in Chapter I.A and I.B exercises with tangent lines and rates you may have already explored the derivative of simple exponential functions. We will continue in this section to describe the derivatives of simple exponential functions more completely.
Let's start with $f(x) = 2^x$ and estimate f '(0). Looking at the graph of this function in Figure I.F.2.1 certainly supports the belief that f has a tangent line and thus that f should have a derivative at 0. Consider the data in Table I.F.2.1. It suggests that $f'(0)= \lim_{h \to 0} \frac {2^h-1}h \approx 0.69315$ .
Leaving this issue for a moment we turn to the derivative of f at a, i.e., f '(a). Here it is to our advantage to use the characterization of the derivative as $f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)}h $. This leads us to examine the difference quotient $ \frac {2^{a+h}-2^a}h=2^a\cdot \frac {2^h-1}h$. Now as we consider the limit as $h \to 0$ we can use the work on f '(0). The fact is that by the definition of the derivative as $h \to 0$ , $\lim_{h \to 0} \frac {2^h-1}h =f'(0)$ . So, to describe f '(a) in general, we see that $$f'(a)= \lim_{h \to 0}2^a\cdot \frac {2^h-1}h = 2^a\cdot f'(0) \approx 2^a \cdot 0.69315$$
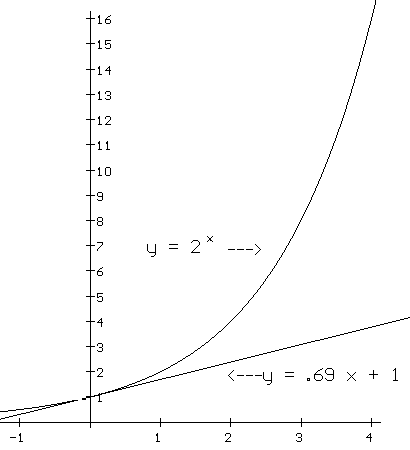 Figure I.F.2.1
Figure I.F.2.1
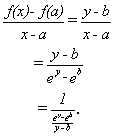 .
.