Summary.....The Big Picture : Log's and Exponential Functions 

Def'n.:   ln(x) = ò1x  1/t dt   [ x>0]	Def'n.:   exp (x) = y Û ln(y) = x  exp(1) º  e [so ln(e) = 1]. exp(x) º ex	Def'n.:  For b >0,   bx º e xln(b).  Note: ln(bx) = x ln(b)	Def'n.:  For b >0,   log b (x) = y Ûx= by
ln(1) = 0  ln(x) > 0 for x >1  ln(x) < 0 for 0< x <1	exp(0) = e0=1  ex> 1 for x > 0  0< ex < 1 for x < 0	b0 = 1  For b > 1:  b x  > 1  for x > 0  0< bx < 1 for x < 0  For 0< b < 1:  b x  > 1  for x < 0  0< bx < 1 for x > 0	log b (1) = 0  For b > 1:  log b (x)>0 for x >1  log b (x)<0 for 0< x <1  For 0< b < 1:  log b (x)<0 for x >1  log b (x)>0 for 0< x <1
ln(A*B) = ln(A) + ln(B)	eAeB =eA+B	bAbB = bA+B	log b (A*B) = log b (A) + log b (B)
ln(A/B) = ln(A) - ln(B)	eA / eB = eA-B	bA /bB = bA-B	log b (A/B) = log b (A ) - log b (B)
ln(Ap/q) =p/q ln(A)	(ex) p/q = e(p/q)*x	(bx) p/q = b(p/q)*x	log b (Ap/q )= p/q log b (A)
ln'(x) = D ln(x) = 1/x  [So ln is continuous and increasing for x >0]	exp'(x) = D(ex) = ex	D(bx) = ln(b) bx	log b'(x) = D log b (x) = 1/( x ln(b))
ò 1/u du = ln|u| + C	òeu du = eu  + C	ò bu du = bu / ln(b) + C	Not relevant!
As x ® ¥, ln (x) ® ¥.	As x ® ¥,  ex® ¥.	b >0: As x ® ¥,  bx® ¥.  b <0:As x ®  ¥ , bx® 0	For b > 1:As x ® ¥, log b (x) ® ¥.  For 0< b < 1:As x ® ¥, log b (x)® - ¥.
As x ® 0+ , ln(x) ® - ¥	As x ® - ¥ , ex® 0	b>0: As x ® - ¥ , bx® 0  b< 0:As x ® - ¥,  bx® ¥.	For b > 1:As x ® 0+, ln (x) ® - ¥  For 0< b < 1:As x ® 0+, ln (x) ®  ¥
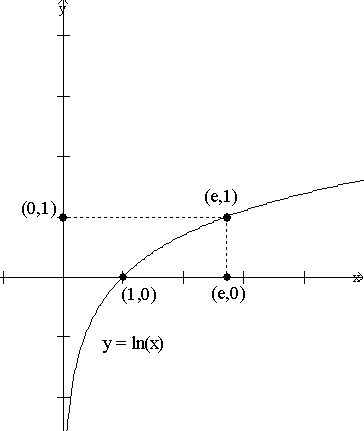
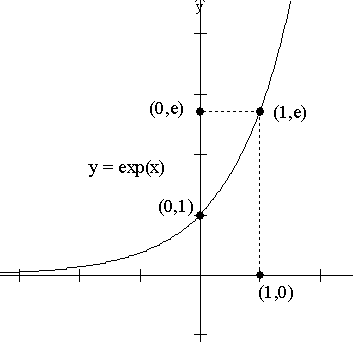
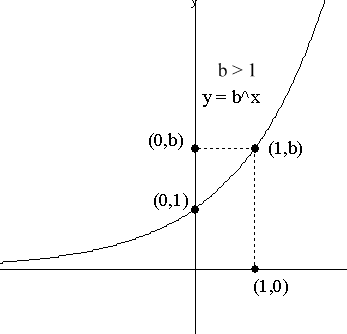
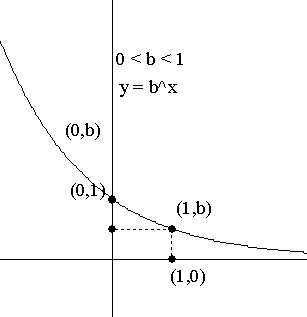
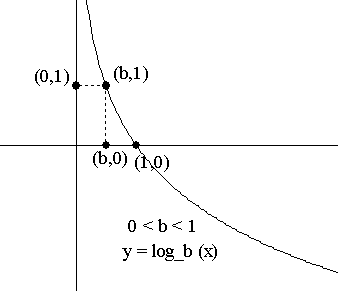