Variables, Constants and Parameters: Using a symbol
to represent a number or any other mathematical object is one of the keys
to the power of mathematics. We have established by convention notations
for numbers that allow us to designate a number by a symbol or a string
of symbols. Once we recognize the distinction between the symbols and
the numbers they represent, we can begin to understand notation being
used to represent a number (or other mathematical object) that is not
known. Perhaps the represented number is characterized by being the solution
of an equation. Perhaps it is a number that corresponds to a measurement
which has not or cannot be made. The meaning or designation of the symbol
can change or vary to suit a context or may be entirely determined by
conditions we may or may not know. It can even be that the symbol is being
used when there is no number that it could possibly represent. This last
situation may be like a discussion of unicorns- these animals do not exist-
yet we can describe them as if they did exist! The symbol can represent
a quantity determined by many known and unknown influences. In other words,
the quantity's numerical value can vary, and so the symbol is called
a
variable
representing a changeable quantity.
The actual use of a symbol to represent a number can depend
on the context. At times a symbol is meant to represent a single number
that will remain the same throughout a discussion. For instance we let
a denote my current age measured in years and
A denote the
amount of money I invested in stocks on January 1, 1996 measured
in dollars. These symbols are called
constants because the quantities
they represent do not change in the context. Letters commonly used for
constants are
a, b, c, d, and
k. At times a symbol represents
a number that will depend on the context, and hence be variable. Yet once
the context has been determined the number will remain constant. We previously
let
a denote my age measured in years and
A the amount of
money I invested measured in dollars. Now these symbols represent numbers
that can vary depending on the specification of more information about
the context. My age depends on the date at which it is measured while
the amount of my investment depends on the time and the form of
investment (stocks, bonds, or a savings account). So these variables can
turn out to be constants depending on the specification of a context.
The word
parameter
is sometimes used to describe a symbol used to represent a quantity that
is variable yet in some investigations will be considered as a constant
determined by the context. The variable
t when used to represent
time is often considered a parameter since we often want to examine the
relation of quantities at a single moment in time, thinking of perhaps
taking a snapshot to record that moment, and thus holding time constant.
Operations, Equalities, and Inequalities: It goes
without saying that much of the mathematics you have studied has dealt
with the arithmetic operations of addition, subtraction, multiplication,
and division and the processes related to determining numbers that will
satisfy relations determined by equations. You will have some review exercises
at the end of this section to check yourself on these skills, including
expanding and factoring polynomials as well as solving linear and quadratic
equations and inequalities. What you may not have considered at length
before is the meaning of these features of mathematics. What does the
statement 2+3=5 mean? Can you explain why `(-2)^4 > 0`?
| Equality as identity of numbers: Let's look first
at 2+3=5. The symbol "=" placed between symbols representing numbers indicates
that the symbols are representing the same number. The idea is that
a single object can be designated in more than one way. You have your
name and your social security number. Usually (but not always) if we look
at the names on a class list there will be only person represented by
that name, and the same is true for the social security numbers on the
list. So we might say that Alice Callahan = 396 23 4583 means that these
symbols designate the same person. On the left side of the equation the
symbol "2+3" represents a single number which results by adding the numbers
2 and 3. On the right hand side we have a number designated by the numeral
"5." The assertion of the equation is that these symbols represent the
same number. This interpretation works just as well to explain `2+3=35/7`.
Both statements are considered true because the symbols on each side of
the equations represent the same number. On the other hand the statement
2+3=7 is false because the symbols on both sides of the equation
do not represent the same number, though it may not always be clear how
we know this.
Equality as defining notation: When we write "let
a be the number with the property that `a^3 = 5` " or "`a=root(3)5`" the equality
sign might be replaced with º which is
sometimes used to reinforce the fact that this use is not asserting an
identity but is establishing a representation. In this case the symbol
a is being assigned to represent any one or more objects that satisfy
the criterion that when cubed the result is 5. Such an object is also
represented by `root(3)5`.
The equation is merely establishing another notational representation.
Equality of expressions involving variables: The
equation x+5=7 may be true or false depending on the interpretation
of the variable x as a specific number. If x is 2
then the equation is true, but if x = 3 (or any other number different
from 2) then the equation is false. But what does the equation mean when
we don't have an interpretation specified for x? An equation with
a variable that does not have a specified value is called an open equation.
An open equation is neither true nor false until the interpretation
of all the variables have been specified. Such an equation serves as a
symbolic form designating a relation between numbers when the variables
are specified. Generally these open equations arise as constraints
characterizing a number or numbers and the problem is to determine
any and all numbers that will make the equation true, i.e., solve
the equation.
|
Inequalities are similar to equations in their meaning.
When we describe those real numbers whose squares are less than 25
we have designated a set of numbers which contains many possible
members. In fact it contains any and all real numbers larger than -5 and
smaller than 5. That seems easy enough to describe, but the issue can
be more subtle when we describe those rational numbers whose squares
are less than 2. In this case the set is a collection of rational numbers
which seems controlled by an irrational number,`sqrt{2}`.
The solutions to inequalities sometimes can be expressed
as intervals of numbers, such as the positive real numbers less than 5.
This interval is denoted (0,5). Recall other examples of notation for
intervals from the following:
| `[2,5]={x:2<=x<=5}` |
`[2,5)={x:2<=x<5}` |
| `(2,5]={x:2<x<=5}` |
`(2,5)={x:2<x<5}` |
| `[2,oo]={x:2<=x}` |
`(2,oo]={x:2<x}` |
| `(-oo,5]={x: x<=5}` |
`(-oo,5)={x: x<5}` |
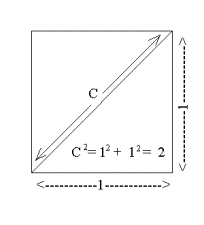
`sqrt{2}`
is not a rational number. As promised earlier in this section, here
is an argument showing that `sqrt{2}`
is not a rational number. The argument proceeds by assuming that `sqrt{2}`
is a rational number and then demonstrating as a result of this
assumption that something absurd and obviously false would also be true.
(This type of argument is described as an indirect argument
or an argument by reduction to the absurd, reductio ad absurdum)
The absurd result with which we will end the argument will be in finding
a number that is both even and odd.
We assume `sqrt{2}`
is a rational number. In fact we assume that`sqrt{2}=
j/k ` where j and k
are integers. Now the defining property for `sqrt{2}` is that
when squared, this number is 2. So it must be that `(j/k)^2 =
{j^2}/{k^2}=2` and therefore ` j^2 =2 k^2`. Now if we consider
`j` and `k` factored completely into products of integers and then
squaring those factors, we see that `j^2` and `k^2`each must have an
even number of 2's for factors (remember 0 is an even number). So the
left hand side of the equation ` j^2 =2 k^2` has an even number of 2's
for factors, while the right hand side of the equation has one more 2
than the even number of 2's appearing as factors of `k^2`, so that we
must conclude by counting the factors that are 2's that some even
number is also an odd number. This ends the argument, since it is
absurd for an integer to be both even and odd.
Review Exercises: The exercises for this section
cover material from previous course work in algebra. You may not
recall all of these topics or how to do the problems precisely. You
should refer to the texts or notes from your previous courses in mathematics
if you find these difficult. The skills and concepts needed to solve these
problems will be important in the work ahead- so be careful to identify
any difficulties you have with these problems and try to remedy any misunderstandings
as you proceed.
Rational Numbers and Repeating
Decimals: It is common to represent fractions using decimal notation.
For instance 1/2 = .5 and 1/4 = .25. More interesting examples require
the use of decimals that continue indefinitely, such as 1/3 = .3333....
or 1/6 = .16666... which indicate that the last digit continues to repeated
in the succeeding decimal places.
- Repeating decimals and rational numbers:
- Find decimal representations for the numbers 2/9, 3/7,
3/11 , and 3/13
- The number that is expressed by the repeating decimal .38383838....
is a common fraction. Here's how to see that algebraically. Let
N=.38383838.... so that 100 N = 38.383838.... . Now subtract
N from 100 N to see that 100N - N = 99N = 38. and so N = 38/ 99.
Study this example, then express the following repeating decimals
as fractions: .535353.... , 5.727272....
, 37.56838383....- Based on part a explain
why .101001000100001.... is not a common fraction.
- Based on part b and
the text's discussion of `sqrt{2}`,
explain why `sqrt{2}`can
not represented by a repeating fraction.
- Review the argument
that `sqrt{2}`
is not a rational number.
- Replace each occurrence
of the number 2 by a 3 in the argument to show that `sqrt{3}`
is also not a rational number.
- Prove that `sqrt{5}`
is not a rational number.
- Discuss why this procedure
fails to show that 2 =`sqrt{4}`
is not a rational number.
- Simplify- express as an
algebraic expression using fewer operations to evaluate for any value
of x that makes sense.
- `{x^2-9}/{x+3}`
- `{x^2+6x+9}/{x+3}`
- `{x^2-2x-15}/{x+3}`
- `sqrt{x^2+6x+9}
- Rationalize
the denominator. a.
`{2+sqrt{3}}/{2-sqrt{3}}`
b. `{2+sqrt{h}}/{2-sqrt{h}}`
- Rationalize
the numerator. a.
`{sqrt{x}-sqrt{3}}/{x-3}`
b. `{sqrt{3+h}-sqrt{3}}/h`
- Determine for which numbers
the expression fails to represent a real number.
a.
`{x^2-9}/{x+3}`
b. `sqrt{x+9}`
c.`{2+sqrt{h}}/{2-sqrt{h}}`
d.`{sqrt{3+h}-sqrt{3}}/h`
7. Solve the following
equations: Find any and all real numbers which the variable can represent
and have the equation be true.
a.
`2x-5=x+3` b. `x^2-2x-5=x+3`
c. `x-3=sqrt{x+3}`
d. `5/{x+3}+4/x=3` e. `x^2+9=4`
8.Solve the following
inequalities: Find any and all numbers which the variable can represent
and have the inequality be true. When possible, express the solution
in interval notation:
a.
`2x-5<=x+3` b.
`x^2-2x-5<x+3` c. `x^2-2x-5>=x+3`
d. `5/{x+3}+4/x>=3`
9.Recall that |a| represents
the magnitude or absolute value of the number a. Thus |a|
is a when a is not negative and -a when a
is negative. For example |5| = 5, while |-3| = 3. Solve the following
equations and inequalities that are expressed using the absolute value.
When possible, express the solution in interval notation:
a. `{|4-x|}/ (4-x) = -1` b. `{|4-x|}/
(4-x) = 1` c.` |x-10000|<1`. d.`|4-x| > 5` e. `|3x
- 6| < 9`
10.Write a short story about
a car trip. Discuss briefly those aspects of the trip that might be measured
and the units and approximate size of the numbers that would arise from
those measurements.
11.Write a short story about
cooking dinner. Discuss briefly those aspects of the meal's preparation
that might be measured and the units and approximate size of the numbers
that would arise from those measurements.
12.Write a short story about
going shopping. Discuss briefly those aspects of the shopping that might
be measured and the units and approximate size of the numbers that would
arise from those measurements.
13.Write a short description
of an ecological system. Discuss briefly those aspects of the system that
might be measured and the units and approximate size of the numbers that
would arise from those measurements.
14.Write a short description
of the human body. Discuss briefly those aspects of the body that might
be measured and the units and approximate size of the numbers that would
arise from those measurements.
15.Write a short story about
an athletic event or sports competition. Discuss briefly those aspects
of the story that might be measured and the units and approximate size
of the numbers that would arise from those measurements.
16.How Ben proved he was
the pope.
Ben arrived yesterday
smiling quite broadly. "I can show you that I am the Pope," he declared
with a laugh. "You see I and the pope are two persons. But I can show
that 1=2, so I and the pope are 1 person. Thus I am the Pope." But you
may ask, "How did Ben show that 1=2?" Here's the argument Ben gave
me.
"Suppose x=y. Then xy = yy,
so xx-xy = xx - yy. Now factoring we see that x(x-y)
= ( x+y) (x-y). Now canceling the common factor of (x-y)
we have x = x+y. But we assumed x=y, so x+y
= x + x = 2x and 1x =2x. Finally we can surely cancel the number
x and we have 1=2. I rest my case! " What is wrong with
Ben's argument?
var
$i
$$able
adj. 1. a . Likely to change or vary; subject to variation; changeable.
b . Inconstant; fickle.
Biology
2. Tending to deviate, as from a normal or recognized type; aberrant
Mathematics
3. Having no fixed quantitative value.
n.
1. Something that varies or is prone to variation.
Astronomy
2. A variable star.
Mathematics
3. a. A quantity capable of assuming any of a set of values
b. A symbol representing
such a quantity. For example, in the expression 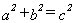 ,
a, b, and c are variables.
,
a, b, and c are variables.
parameter
n. 1. Mathematics a . A constant in an equation that varies in other equations
of the same general form, especially such a constant in the equation of
a curve or surface that can be varied to represent a family of curves
or surfaces.
b
. One of a set of independent variables that express the coordinates of
a point.
2. a . One of a set of measurable factors, such
as temperature and pressure, that define a system and determine its behavior
and are varied in an experiment.
b.
A factor that restricts what is possible or what results: All the parameters
of shelter where people will live, what mode of housing they will choose,
and how they will pay for it. New York
c
. A factor that determines a range of variations; a boundary: an experimental
school that keeps expanding the parameters of its curriculum.
Statistics
3. A quantity, such as a mean, that is calculated from data and
describes a population.
4.
A distinguishing characteristic or feature.