Sensible Precalculus: Algebra and The Elementary Functions
© 2000 M. Flashman.
Chapter 1: Introduction, Background, and Other Goodies
A. Why Precalculus- instead of More Algebra and Trigonometry?
 
There are all too many books with titles using the term "Precalculus" or "College Algebra with Trgonometry" and courses with the same titles to think that this is the first time you have seen these words. Hey, you're in some kind of a precalculus course right now! But do you know why the subject is called "precalculus" and precisely what it is? The answers are not as simple as saying, " it's the course you take before you take calculus." To begin I'll try by telling you something about the background of calculus (as I understand it) before the word "calculus" was identified as a specific subject area of mathematics. Then the explanation of "precalculus" will be connected to the calculus: precalculus mathematics is mathematics that gives background for the mathematical concepts, problems, issues and techniques that appear in the calculus course. 
What is "calculus"? Quite simply a "calculus" is a method for systematically determining a result, for arriving at a conclusion, or (if you don't mind the redundancy) for calculating an answer [1]. In this sense there are many calculi, such as the calculus of propositional logic, the calculus of set operations, the calculus of probabilities, etc.  But when someone talks about "The Calculus," be it "differential" calculus, "integral" calculus, or the calculus of infinite series, the reference is usually to "The Calculus of Isaac Newton (1642-1727) and Gottfried Leibniz (1646-1716)."  This calculus provides procedures for solving problems in the analysis of change: determining rates of change, predicting the amount  and explaining the quality of change, and connecting the concepts of change with the language and symbolism of algebra that describes change. This calculus also develops tools for solving problems of geometry: determining a line tangent to a curve or finding the area of a planar region, predicting the shape and explaining the graphic qualities of a curve, and connecting these geometric concepts to the language of algebra that describes geometry.
Since its early development, calculus has grown more important. Its analysis has been applied in many contexts: the physical sciences and engineering, the life sciences,  economics, probability.  In fact calculus has uses in practically any area of study where change is important. It provides a theoretical basis as well as a practical tool for exact and estimated solutions to problems in almost every scientific disciplines.
Before Newton or Leibniz, several great mathematicians had studied many of the physical and geometric questions, from Euclid and Archimedes in antiquity to Descartes, Fermat, and Pascal to name only a few mathematicians living within the century before Newton. Newton and Leibniz differed from those who had worked on these questions before them by achieving a general overview to the problems. Their approaches, developed independently, solved the problems using systematic techniques of calculation that depended fundamentally on the algebraic description of the problem. With these techniques the user could avoid repetitious conceptual analysis of each different  curve or formula. The conceptual analysis was summarized in the justifications of the calculus rules, which were the primary achievement of the new calculus. The results for the actual problems contained in works by Newton and Leibniz may not have been new, but the methods were revolutionary in their generality. 
Let's touch briefly on two geometric problems that were historically important to the development of the calculus: The tangent problem and the area problem. 
The Tangent Problem: You may recall a geometric method, known at least since the time of Euclid (about 300 B.C.E.) for drawing a line that touches a circle C only at one specific point, P, on the circle. [ See Figure 1.] This line is called the tangent line to the circle C at P. The construction of this line involves two simple steps: i) draw a radius from the center of the circle, O, to the point P; and ii) construct a line at P that is perpendicular to the radius OP. This perpendicular line is the desired tangent line.
A similar problem for a parabola was solved by Archimedes, (c. 287 B.C.E. - 212 B.C.E.) The problem is to find a method for drawing a line that touches a parabola R only at one specific point, P, on the parabola. [See Figure 2.] This line is called the tangent line to the parabola R at P. 
The general tangent problem is a little more difficult to state because the quality of being tangent in general requires a more subtle characterization. Ignoring the issue of what "tangent" means for now, we can describe the general tangent problem as the problem of finding a method for drawing a line tangent to a curve at a specific point P on the curve.
 
The Area Problem: The area problem is perhaps more familiar as a measurement problem today. No doubt you have learned many formulae for finding the area of such common planar regions as those enclosed by squares, rectangles, triangles, trapezoids, and circles. Earlier treatments of area had a geometric constructive flavor with which you may not be so familiar.
 
 
For example, the area problem for a right triangle is to give a method of constructing a rectangular region with area equal to that of a given right triangle. Here the geometric solution follows two steps: i) Bisect one leg of the right triangle. ii) Form  a rectangle with one of the resulting segments and the other leg. This rectangle has the desired property.
The statement of the general area problem in geometry is to give a procedure for constructing a rectangle (or square) with an area that is the same as the area of a given region in the plane.
The connection between geometry, numbers, and algebra is generally considered one of the major contributions of the French mathematician, scientist, and philosopher, René Descartes (1596-1650) though some of the ideas appeared in earlier works of Oresme and Galileo. Once measurement and algebra are added to the tools with which we analyze the area problem, we arrive at a familiar formulation of the right triangle area result. If the legs of the triangle have lengths a and b then the area A of the triangle (and the rectangle) is 1/2 a b.  If we use x instead of a for the length of one leg and mx instead of b for the other leg then we have the area determined by the numbers m and x.
 
 
Newton and Leibniz both developed algebraic methods for a calculus of tangents and with that they were able to explore algebraic methods to find a calculus that would systematically resolve many problems of area, as well as problems of volume, arc length, etc.
What then is the calculus? Briefly again, calculus is a conceptual framework which provides systematic techniques for solving problems suitably posed in the language of analytic geometry and algebra.
What kind of problems can be solved using calculus? Some problem types frequently mentioned in discussions of the calculus over the centuries of its development are quite easy to characterize. Other problems have been developed in the past century or so as a result of the expansion of the use of mathematics beyond the physical sciences of physics, chemistry, and engineering, into disciplines such as biology, medicine, and economics. The increased importance of probability and statistics in understanding all of the sciences has also resulted in bringing  other issues of the calculus into the limelight. Here is a short list  of some traditional and non-traditional problems that use the calculus. 
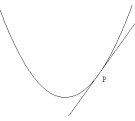
  1. The Tangent Problem. Determine the line tangent to a given curve at a given point. (Also, 1a: Define precisely the concept of "tangent.") For example, determine the line in the plane tangent to the circle with equation X 2 + Y 2 = 25 at the point (-4,3).
  2. The Velocity Problem. Determine the instantaneous velocity of a moving object. (Also, 2a: Define precisely the concept of "instantaneous  velocity.") For example, determine the instantaneous velocity of an object moving on a straight line at time t = 5 seconds when its position at time t seconds is t 2 + 6t meters from a given point P.
  3. The Extremum Problems. Determine the maximum and minimum values of a variable quantity that is dependent upon another variable quantity. For example, suppose the variable Y depends on the variable X with Y =  X 2 - 6X. Determine any maximum and minimum values for the dependent variable Y when the variable X is allowed to vary over real numbers between 0 and 10.
  4. The Area Problem. Determine the area of a planar region enclosed by a suitably defined curve. For example, determine the area of the planar region enclosed by  the X - axis, the lines X = 2, X = 5, and the parabola with  equation Y =  X 2 - 6X.
  5. The Arc Length Problem. Determine the length of a suitably defined curve. For example, determine the length of the parabola with equation Y =  X 2 - 6X between the points (0,0) and (6,0).
  6. The Tangent Curve Problem Reversed. Determine a curve so that the tangent to the curve at any point on the curve is predetermined by some description depending on the point's position in the plane. For example, determine a curve in a coordinate plane so that the slope of the tangent to the curve at the point (a,b) is a + b.
  7. The Position Problem. (The Velocity Problem Reversed.) Determine the position of an object moving on a straight line from knowledge of its initial position and instantaneous velocity at every instant. For example, determine the position of an object moving on a  straight line at time t = 5 seconds knowing its initial position is P on the line and its instantaneous velocity at time t is precisely t 2 - 6t meters per second.
  8. The Growth/Decay Problem. Given the size of a population or populations and the rates of growth or decay of the population(s) as functions of the time and current population sizes, describe the size of the population(s) in the future or in the past. For example suppose a population is measured by its biomass and it currently has a biomass of 1000 kilograms. Suppose the population is growing at a rate that is proportional to its current size  and that one hour ago its biomass was 950 kilograms.  Find the biomass in 10 hours. Find how long it will take before the biomass will be 2000 kilograms, 5,000 kilograms, and 10,000 kilograms.
  9. The Probability Expected Value - Mean Problem. In an experiment where we measure the outcome of a variable X, suppose the probability that X< A is given by some function F(A). What is the expected value of X? that is, what number in theory would be close to the average or mean of the values for X if the experiment is repeated a large number of times. For example, suppose we throw a magnetic dart at a circular dart board of radius 2 feet and we measure X as the distance from center of the board to where the dart lands. Suppose that the probability that X< A is given by the function F(A)= A2/4 for 0< A < 2; 0 for A < 0; and 1 for 2 < A. What is the expected value of X? that is, what is the expected distance of the dart from the center of the target?


    10. Precalculus Mathematics: So now that you have a better idea of what mathematical problems are connected to the "calculus," what is "precalculus" mathematics? Here the simple answer we gave earlier can be expanded.  Precalculus mathematics is mathematics that gives background for the mathematical concepts, problems, issues and techniques that appear in the calculus course. Certainly one key background tool for the calculus is the function concept. Being familiar with function concepts and specific functions provides an important foundation and language for the calculus.

    To understand calculus you should have a background that allows you to use

    1. numbers and variables in the context of algebra,
    2. equations and functions both algebraically and visually, and
    3. "real world" applications that use functions to relate the quantities involved.
    So what is the sensible approach to prepare you for calculus? In the sensible precalculus approach we will
    1. Review and renew your understanding of numbers and variables as used in algebra.
    2. Review and renew your understanding of equations both algebraically and visually.
    3. Review, renew, and expand your understanding of functions both algebraically and visually.
    4. Connect "real world" applications to the equations and functions we introduce here.
    5. Introduce problems of the type encountered in calculus when precalculus techniques can be used for solution.
    6. Introduce methods from current technology that will make precalculus analysis easier and form a foundation for later calculus use of technology.
[1] From the Complete Reference Library Dictionary, Mindscape. The American Heritage Dictionary of the English Language. 3rd Edition, 1980, Houghton Mifflin.
Calculus   a . The branch of mathematics that deals with limits and the differentiation and integration of functions of one or more variables.
b . A method of analysis or calculation using a special symbolic notation.
c . The combined mathematics of differential calculus and integral calculus. A system or method of calculation.[ Latin, small stone used in reckoning]