973-C1-513
Monday January 7, 2002, 10:30 a.m.
MAA Session on Integrating Mathematics and Other Disciplines, II
 
 

Martin E Flashman
flashman@humboldt.edu
Humboldt State University
Dept. of Mathematics
Arcata, CA 955521.

Using Probability to Understand Calculus

Abstract:
Calculus courses often refer to probability in a limited role as an application. The author will discuss using probability systematically in a calculus program to enhance the understanding of differential, integral, and series calculus. (Received September 14, 2001)

Preface: A traditional approach to calculus uses two interpretations for most of the calculus concepts: An additional interpretation based on probability concepts provides a strong alternative that has the advantage of integrating the scientific issues of randomness that are basic to most scientific disciplines with the mathematical concepts of the calculus.

Though probability is presented briefly in calculus books in a single section or two, no current calculus text has treated probability as an interpretation or application that presents the calculus concepts consistently along with those of probability.

This work is connected toThe Sensible Calculus Program.

Below are several examples illustrating how probability concepts can work as interpretations compared with the more traditional interpretations.


 

Motion [Geometry] Interpretation Probability Interpretation
 0.Generic Example(s) and Precalculus concepts: Functions and Rates. Motion of an object.
Position functions.
Constant velocity.
Average velocity. 		 Measurement of a random variable.
(Cumulative) Distribution functions. 
Uniform distribution functions.
Average Probability Density.
 I.  The Derivative. Position functions determine velocity functions as limits of average velocity. Distribution functions determine density functions as limits of average probability density.
II.Applications of continuity and derivative analysis. Midway point, Maximum velocity, Mean velocity. The Median, Mode, and Mean.
III. Differential Equations. Initial Value Problems Boundary Value Problems
IV.The Integral. Velocity determines position functions. 
The mean value theorem for integrals.		 Density functions determine distribution functions.
The mean value of a random variable.
V. Variation and Integration. Volume Of Revolution for graph of Y=f (x) about Y= b. Variation of the value of the random variable from the mean.
VI. Infinite Series. Accumulation of discrete changes in position. Zeno  Discrete distributions and point density functions.

 
 
0.Generic Example(s) and Precalculus concepts: Functions and Rates..
Measurement of position of an object.
Measurement of a random variable.
Position functions. y = s(t)
(Cumulative) Distribution functions.
y = F(x) = Probability that the value of the random variable is less than  (or equal to) x
.
Constant velocity. Ds(t) = k Dt
Uniform distribution functions.DF = k Dx
Average velocity over the interval [a,b]
v[a,b] = [s(b)-s(a)]/ [b-a]
Average Probability Density for X in [A,B] 
f [A,B] = [F(B)-F(A)]/ [B-A]
Random Variable : X = distance of dart from center of unit dart disc.

Probability Distribution Function for X:   F(A) = Pr( X < A)


 1          1£A
F(A) = Pr( X < A)  =  A2    0£A<1

0          A<0


Average Probability Density for X on [A,B]:
f [A,B] = Pr(A<X<B)/(B-A) = (F(B)-F(A))/(B-A)

0<A<B<1       f [A,B] = Pr(A<X<B)/(B-A)= (B2 -A2)/(B-A) = B+A

 I.  The Derivative.
Position functions determine velocity functions as limits of average velocity.
Distribution functions determine density functions as limits of average probability density.
Instantaneous velocity at the point x=a
v(a) = lim [s(x)-s(a)]/ [x-a]
x->a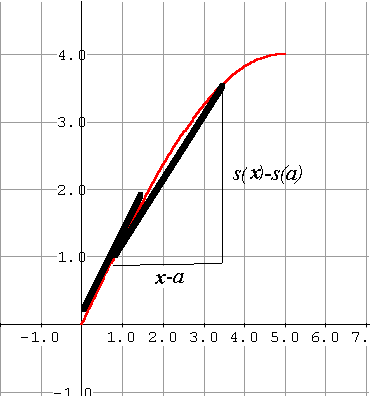 
Point Probability Density for X at X=A
f (A) = lim [F(X)-F(A)]/ [X-A]
X->A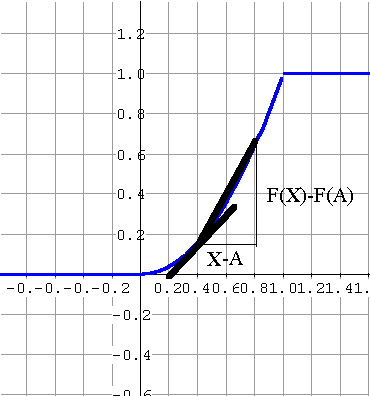 
Probability Density for X at A :
f (A)= F '(A)= lim  f [A,B]
              B ->A 

A < = 0                   f (A)=0 

0<A<1    f (A)= F '(A)= lim f [A,B] = lim    B+A = 2A
                     B->A            B->A

1<A                     f (A)= 0 


 
II.Applications of continuity and derivative analysis.
Midway point
If s is continuous on the interval [a,b] 
there is a time t*  in [a,b] where s(t*) is midway between s(a) and s(b).
Median
If F is continuous on the interval [A,B] there is a value M in [A,B] where F(M)=1/2.
M is called the median of the random variable.
Maximum velocity
If v  is continuous on the interval [a,b] 
there is a time t*  in [a,b] where v(t*) is maximal.[Maximal velocity]
 Mode
If f  is continuous on the interval [A,B] 
there is a value M*  in [A,B] where f (t*) is maximal.[Maximal density]
M is called the mode of the random variable
Mean velocity
If s is continuous on [a,b] and differentiable on (a,b) then there is a time t* where v(t*)[b-a]=[s(b)-s(a)]
Mean density
If F is continuous on [R,S] and differentiable on (R,S) then there is a value X* where f(X*)[S-R]=[F(S)-F(R)]
                         = Prob( R<X<S)
Median for X: M    F(M)= 1/2.
M2 = 1/2 
M = sqr(2)/2

Mode for X: m      f (m) is maximum value.
m = 1 (?)


 
III. Differential Equations
Initial Value Problems: Given velocity as a function of time and an initial position, find the position as a function of time.

Given  v(t)=s'(t) and s(0)=a.
Find s(t).		 Boundary Value Problems: Given the density as a function of the random variable X on the interval [A,B], find the distribution as a function of the value of the random variable X.

Given f (x) = F'(x) with F(A) = 0 and F(B)=1. When possible find F(x).
 Given f (x) = 2x = F'(x)
F(x)=x2 +C
F(0)=0, F(1)=1; so F(x)=x2
IV.The Integral.
Velocity determines position functions.
s(t) - s(a) = òat  v(t) dt
Density functions determine distribution functions.
F(B) - F(A) = òAB f (x) dx
= Prob( A<X<B)
The mean value theorem for integrals.
If v is continuous on [a,b] there is some t* where
v(t*)[b-a] = [s(b)-s(a)] = òab  v(t) dt
 
The mean value of a random variable.
Estimate: S{xk  [F(xk)-F(xk-1)]} 
or  S{xkf(xk)  [xk - xk-1]}
The mean of the random variable X is 
m = òAB  x f (x) dx.
The average value of the velocity is 
òab  v(t) dt/[b-a].
Note: For the uniform distribution 
f(x) = 1/[B-A]. Thus for the random variable X, 
the mean of the random variable is 
m = òAB  f (t) dt/[B-A].
Pr(A<X<B) = F(B) - F(A)

=òAB f (x) dx  =  òAB 2x dx  =  B2 -A2


Mean for X: m = ò01  x f (x) dx 
= ò01  x (2x) dx = 2/3.


 
V. Variation and Integration. [Skip for time]
Volume of revolution for graph of Y=f(x) about Y= b.
V = pòab(f(x)-b)2 dx.
Variation of the value of the random variable X from the mean.
Var(X)  =  òab(x-m)2f(x)dx

=  òab  x2 f(x)dx - 2mòab x f(x)dx +  òabm2f(x)dx

= Exp(X2 ) -  m2
VI. Infinite Series.
Accumulation of discrete changes in position. Discrete distributions and point density functions.
Suppose Dsk is the net change in position during the kth interval of time. 

Find the total change in position for an infinite sequence of time intervals.

S= S0¥Dsk.

Example (Zeno) 
Dsk = 1/2k. S =1.
Geometric Series: Dsk = r,
S =1/(1-r)      for -1<r<1.
 
 
 

 

 Suppose pk = Pr(X=k)>0 only if k is a natural number. Then S0¥ pk = 1.

Example: pk=prob that first H occurs on the kth toss of a coin 
where Pr(H)=p and Pr(T)=q=1-p. 
Thus pk=pqk-1. 
Then S1¥pk = S1¥ pqk-1= p/(1-q) = 1

Mean of a discrete random variable: 
m = S0¥ kpk.

Example: 
m = S0¥ k pqk-1= p S0¥ kqk-1
=p S0¥ Dqk =pD(S0¥ qk ) = 
=pD(1/(1-q)) = p / (1-q)2 = p/p2 
=1/p.

thus if p = 1/2, m = 2;
p = 1/5, m = 5.

The End
The Sensible Calculus

http://flashman.neocities.org

flashman@humboldt.edu