- Symbols , words, and other designations.
- Various Arabic numerals
- Roman Numerals I, II, III, IV, V, VI, VII
- Egyptian numerals
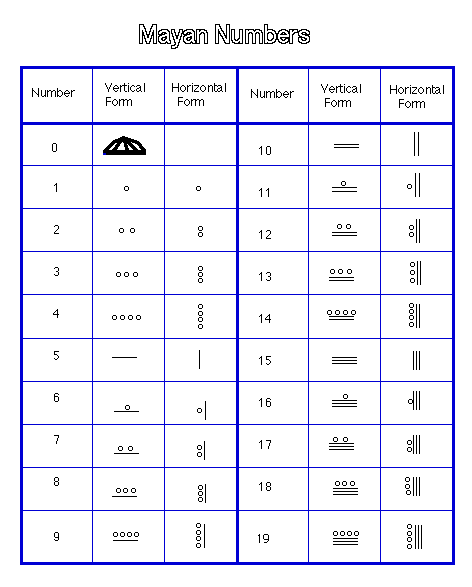
- Mayan Numerals
- Binary Notation: 1,10,11,100,101,110,111
- Different Languages: ....
- What defines the number 7? Webster's definitions.
Examples of numerals for the number seven.



Encyclopedia Britannica .
- On a calendar.
- On a color wheel.
- In games and sports.
- 7 fielders in baseball (not part of the "battery").
- 7 players in indoor soccer
- 7 line players in football
- 7 card poker games (7 card stud and Texas Hold'em)
- In mystical/religious writings
- lucky 7
- 7 deadly sins.
- In music and dance:
- The seven notes of a diatonic scale.
- The dance of the seven veils.
- In literature:
- The House of Seven Gables
- Seven Samurai
- Seven Brides for Seven Brothers
- Snow White and the Seven Dwarfs
- In geography:
- The seven seas.
- The seven (?) continents.
- The seven wonders of the world.
- In committee organization:
The HSU Math department has 7 standing committees.
Personnel
Kieval Lecture Scholarship/prizes
Curriculum
Technology
Statistics
Teacher Preparation
- By itself.
- A cardinal number of a set.
- An ordinal number from an ordered set.
- By its unique properties:
- By recognizing its qualities in a variety of contexts.
- Common
- Mathematical
The unique number such that .....