2. Marginal Concepts: Understanding the analysis of critical points.
|
|
|
 |
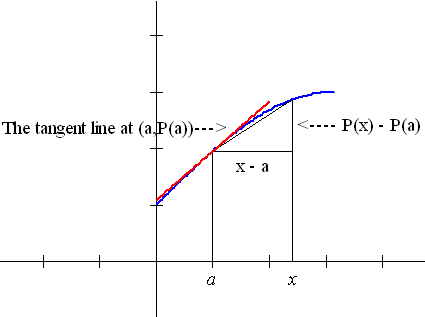
y = P(x) = Profit [revenue or cost]for producing x units. x measures the production or sales level. .  |
|
∆s(t) = k ∆t
 |
Uniform (Constant per unit) profit functions

|
|
v[a,b] = [s(b)-s(a)]/ [b-a]  |
AP[a,b] = [P(b)-P(a)]/ [b-a] 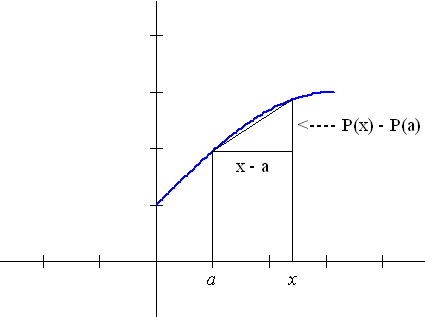 |
|
|
|
|
v(a) = lim [s(x)-s(a)] / [x - a] 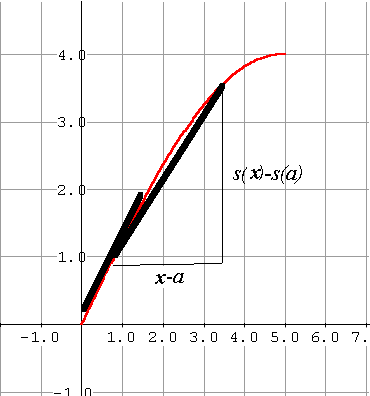 |
P'(a) = MP(a) = lim [P(x)-P(a)]/ [x-a] |
| Constant Multiple and Sum Rules: M(a P(x)) = a MP(x)
Change in monetary scale measuring profits. C(x) = C1(x) + C2(x), then
If cost has two components, MC(x) = MC1(x) + MC2(x) then the marginal cost is the sum of the marginal costs of those components. P= R-C
The marginal profit is composed of the marginal revenue less the marginal cost.MP = MR - MC. Product and Quotient Rules: R = p*x
The rate at which revenues change with respect to time
is determined by the rate at which the price is changing and the rate at
the level of sales is changing.dR/dt = x*dp/dt + p*dx/dt AvP = P/x so
The Marginal average price is determined by the average of the marginal price less the average price. MAvP = MP/x - P/x2 = MP/x - AvP/x = [MP - AvP]/x Chain Rule: dR/dt = dR/dx * dx/dt = MR * dx/dt
The rate of change of revenue over time is determined by the product of the marginal revenue and the rate at which the level of sales are changing. |
|
| Position moving up-increasing: ds/dt >0 Position moving down- decreasing: ds/dt <0 |
Profit moving up-increasing: dP/dx >0 Profit moving down- decreasing: dP/dx <0 |
| Extreme position. ds/dt = 0 |
Extreme profit: dP/dx = 0 |
|
Applications
Maximaizing Profit: Since P = R- C. A necessary condition for maximal profit is that MR = MC.Maximizing Revenues: Suppose a relation between price (p) and sales (x) ... usually described as "the demand curve." R = p*x
So dR/dx = p + x * dp/dx.
So maximal revenues occur when 0 = p + x * dp/dx or
-x/p*dp/dx = 1
or from the differential point of view when dx/x = -dp/p.
From an economics point of view: -x/p*dp/dx = - [dp/p]/[dx/x] is called the elasticity of demand...
indicating the relation of a percentage change in price to a percentage change
in sales.The economic statement: A necessary condition to achieve maximal revenues at a given price is that the elasticity of demand at that price must be 1. The economic argument: If not so, then one can adjust the price up or down to improve revenues since a greater or lesser price by a small percentage will give larger or smaller percentage change in sales and thus larger revenues. |
|
The Mean Value Theorem: At some point in time the instantaneous velocity is the average velocity. |
|
Mean velocity
:If s is continuous on [a,b] and
differentiable on (a,b) then there is a time t* where v(t*)=[s(b)-s(a)]/[b-a]
|
Average Profit: If P is continuous on [a,b] and
differentiable on (a,b) then there is a level of production x* where MP(x*)=[P(b)-P(a)]/[b-a] |
| Initial Value Problems: Given velocity as a function
of time and an initial position, find the position as a function of time.
Given v(t)=s'(t) and s(0)=a. Find s(t). |
Initial Value Problems: Given the marginal cost as a function
of the level of production x and the fixed costs, find the cost as a function of the level of production.
Given f (x) = C'(x) with C(0) = C0. Find C(x). |
| Euler's Method interpreted as estimating the position based on the velocity function and the initial position.
|
Euler's Method interpreted as estimating the cost based on the marginal cost function and the fixed cost. |
| Use Euler to estimate the net change in position s for a time interval [a,b]. By definition, Euler also estimates ∫ab
v(t) dt .
So ... = s(b) - s(a).
|
Use Euler to estimate the net change in costs C for a production interval [a,b]. By definition, Euler also estimates ∫ab MC(x) dx
.
So ... = C(b) - C(a). |
|
Application- Qualitative Analysis related to a Differential Equation
The Evans Price Adjustment Model:If the price is not at equilibrium, then it will change over time so that its rate of change, dp/dt, is proportional to the shortfall, that is dp/dt = k (D(p) -S(p)).
|
|