Section TRIG Trigonometric Functions
Introduction: Of all the functions
that are studied, the most geometric class of core functions is the class of trigonometric
functions. These functions are
characterized by their evolution from the geometry of similar triangles. Paired with these
functions are their inverses, the inverse trigonometric functions.
For example, the sine function evolved from a
right triangle with a specified acute angle, $\alpha$, by finding
the ratio of the length of the side opposite the angle, $a$, to
the hypotenuse, $c$: $\sin(\theta) = \frac a c$. Traditionally
when a triangle is used the angle is measured in degrees.
Eventually the sine function is applied to any oriented angle and the
angle is measured by a real number, $x$ or $t$, described as radian
measure. This angle measurement can be interpreted as an oriented arc on
a circle with radius of measurement a unit of length. The ratio
that defined the sine of the angle for a right triangle then can be
measured in a cartesian coordinate plane as the second coordinate of the
end point of the arc when the circle has
center at $(0,0)$ and the initial point for the oriented arc has
coordinate $(1,0)$.
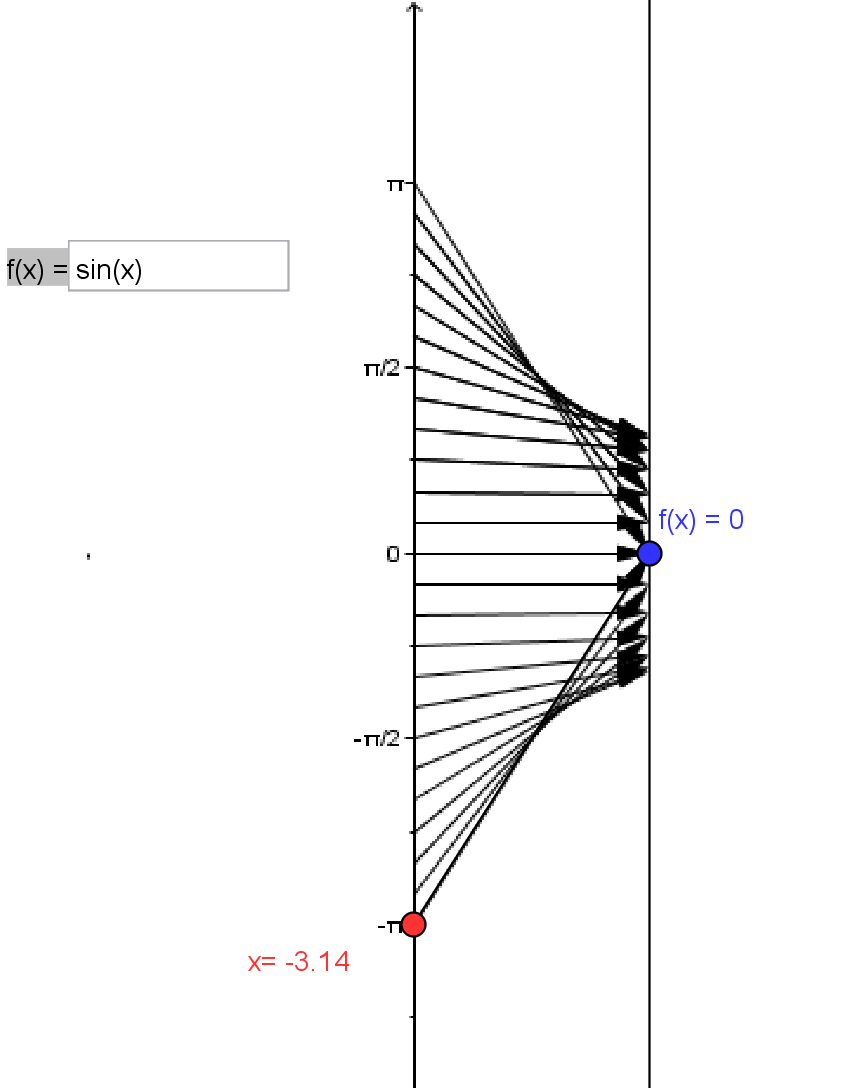
So if the coordinates of the end point of the oriented arc of length $t$ are given by $(x(t),y(t))$ then the sine function is defined by $f(t) = \sin(t) = y(t)$, also represented symbolically as $\sin: t \rightarrow \sin(t) = y(t)$. This function when restricted to angles measured in radians in the interval $[-\pi,\pi]$ is visualized by the mapping diagram, TRIG1.
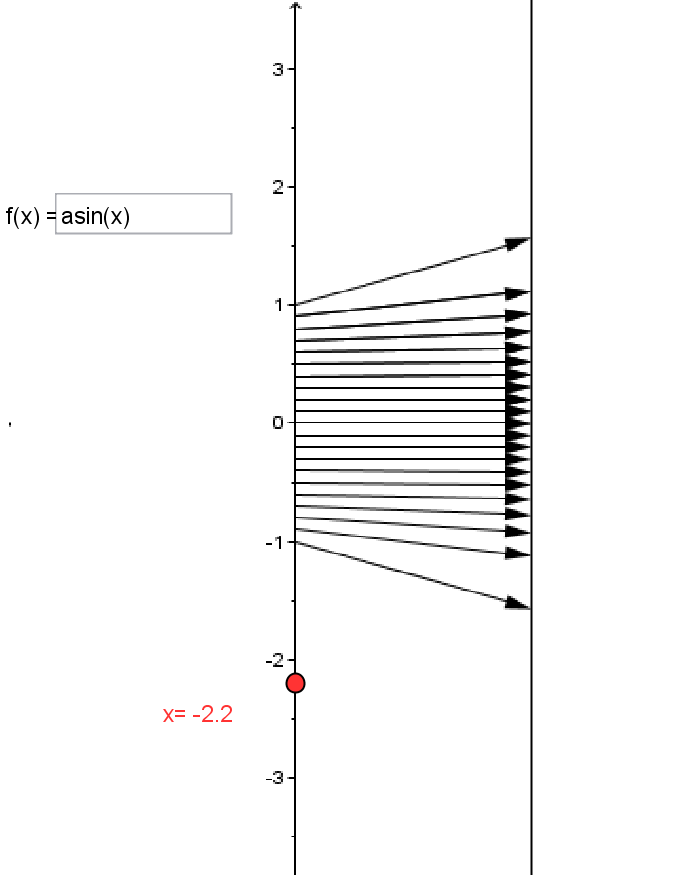
The inverse function for $f(t) = \sin(t)$ is called the inverse sine function or arcsine function. It is traditionally denoted either $arcsin$, $asin$ or $sin^{-1}$.
For this function to make sense the domain of the sine
function is restricted to the interval $[-\pi/2,\pi/2]$. This
function is also represented symbolicly as $sin^{-1}: x
\rightarrow sin^{-1}(x)$, or verbally by saying "to
find $\sin^{-1}(x)$ or $\arcsin(x)$ , find the number (measuring an angle in radians) $t$ where $-\pi/2 \le t \le \pi/2$ and $\sin(t)$ is $x$".
The domain of $\arcsin$ is
$[-1,1]$ and it satisfies the inverse function
defining property:
or,
$\arcsin(\sin(t))=t$ and $\sin(\arcsin(x)) =x$.
 |
|
|
Mapping Diagram TRIG1
|
Mapping Diagram TRIG2 |
This section will provide examples, explanations, exercises and problems that will help students use the power of the mapping diagram along with the three other tools (equations, tables , and graphs) to understand trigonometric functions.
TRIG.TRIGI Trigonometric Functions are Important. (Not Yet Done)
The following example presents the sine function $\sin(x)$ and the
cosine function $\cos(x)$ with a table of data, a graph and a mapping
diagram for each.
Example TRIG.0
The First Trigonometric Functions Example [Graphs and Mapping Diagrams].
Definition TRIG.DEF : Trigonometric Function Definitions
Definition TRIG.INV: Inverse Trigonometric Function Definitions
Treatment of trigonometric functions and their graphical interpretation are familiar. [See wikipedia.org/wiki :trigonometric_function]
They appear in every textbook that deals with trigonometry and preparation for calculus. What is missing is a balanced treatment using mapping diagrams to reinforce the function aspect of visualization. That will be emphasis of this section.
Comparisons will be made when appropriate to graphs- but we will develop the basic concepts for trigonometric functions with mapping diagrams. The end of this section includes some powerful and different ways to think about trigonometric functions and the ways they are represented algebraically.