Section IN Exp and Log Functions
Introduction: Of all the functions
that are studied, after algebraic functions. the
simplest class of core functions is the class of exponential
functions. These functions are
characterized by the appearance of a variable quantity in
the exponent with a constant base. Paired with these
functions are their inverses, the logarithmic
functions.
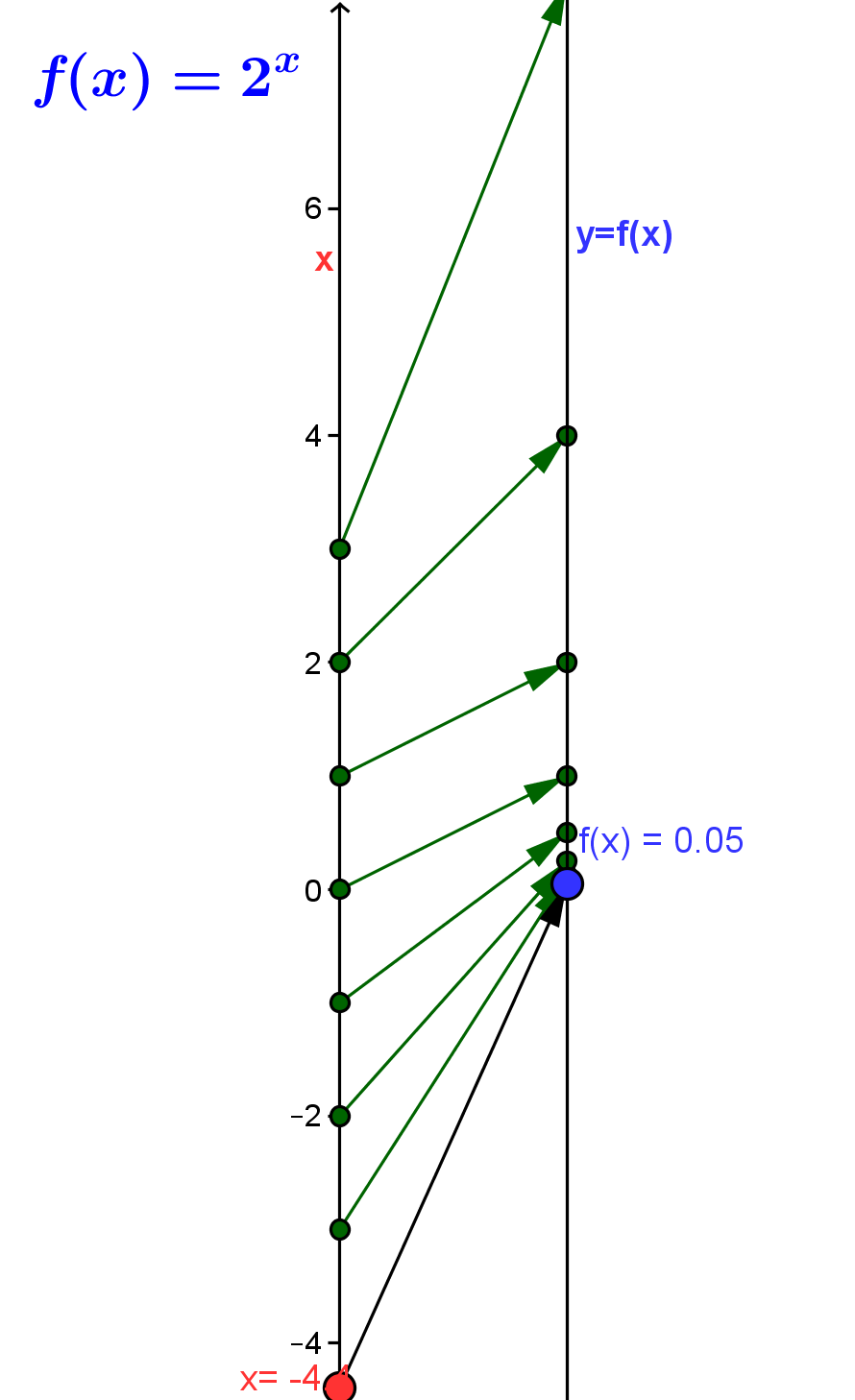
For example, the function defined by assigning the value $f(x) = exp_2(x) =2^x$ to the number $x$, also represented symbolically as $f: x \rightarrow exp_2(x) = 2^x$, or verbally by saying "to find $f(x) = exp_2(x)$, raise the number $2$ to the $x$ power", is described as an exponential function. The number $2$ is described as the base of this exponential function. This function is visualized by the mapping diagram, ELF1.
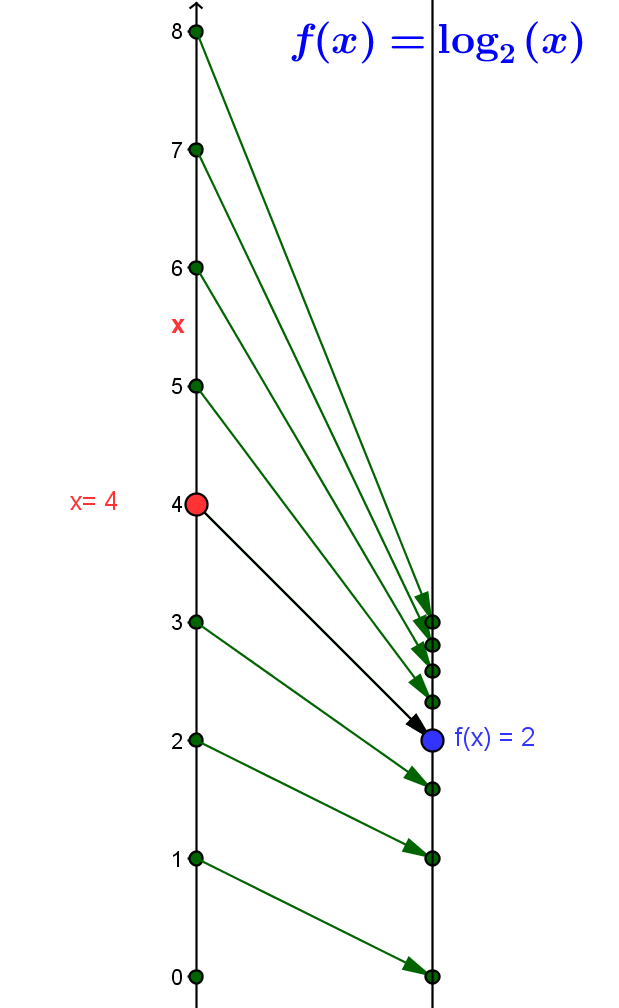
The inverse function for $f(x) = 2^x = exp_2(b)$ is called the logarithm function, traditionally denoted $log_2$. This function is also represented symbolically as $f: x \rightarrow log_2(x)$, or verbally by saying "to find $log_2(x)$, find the number $y$ where $2$ to the $y$ power is $x$". The domain of $log_2$ is $(0,\infty)$ and it satisfies the inverse function defining property:
For all $a \in R$ and $b \in (0,\infty )$,or,
$log_2(exp_2(a))=log_2(2^a)=a$ and $exp_2(log_2(b)) = 2^{log_2(b)}=b$.
 |
|
|
Mapping Diagram ELF1
|
Mapping Diagram ELF2 |
This section will provide examples, explanations, exercises and problems that will help students use the power of the mapping diagram along with the three other tools (equations, tables , and graphs) to understand exponential and logarithmic functions.
Exponential Function Definition
Logarithmic Function Definition
ELF.ELFIExponential and Logarithmic Functions are Important. (Not Yet Done)
This example presents the exponential function $f(x) = 2^x$ and the logarithmic function $g(x) = log_2(x)$ with a table of data, a graph and a mapping diagram for each. The "base" in both examples is $2$.
Treatment of exponential and logarithmic functions and their graphical interpretation are familiar. [See wikipedia.org/wiki : exponential_function / logarithmic function]
They appear in every textbook that deals at all with intermediate algebra - from algebra II to beginning calculus. What is missing is a balanced treatment using mapping diagrams to reinforce the function aspect of visualization. That will be emphasis of this section.
Comparisons will be made when appropriate to graphs- but we will develop the basic concepts for exponential and logarithmic functions with mapping diagrams. The end of this section includes some powerful and different ways to think about exponential and logarithmic functions and the ways they are represented algebraically.